GENERALIZED KERNEL AND MIXED INTEGRAL EQUATION OF FREDHOLM - VOLTERRA TYPE

Abstract

In this work, the existence of a unique solution of mixed integral equation (MIE) of the second kind is considered, in the space ( ) [0, ] p L  C T , where  in the domain of integration and t [0,T ] is the time. The kernel of position is considered in a generalized potential form. A numerical method is used to obtain system of Fredholm integral equations (SFIEs). The existence of a unique solution of this system can be proved. Finally, many special cases are considered and established from the work and some numerical results are considered

Keywords

Fredholm- Volterra integral equation (F-VIE), generalized potential kernel, degenerate method, linear algebraic system.

MSC: 45 B05, 45G 10, 65R

INTRODUCTION

Many problems of mathematical physics, engineering and contact problems in the theory of elasticity, fluid mechanics and quantum mechanics lead to one of the form of the integral equations. In [1], Abdou used the separation of variables method to solve the F-VIE of the first kind in the space , where  in the domain of integration in position, and is the time. The monographs of [2, 3] contain many spectral relationships which are obtained, using the orthogonal polynomial method and potential theory method. In [4], Abdou obtained the spectral relationships for the F-VIE of the first kind in three dimensional. The kernel of FI term is considered in a generalized potential form, while the kernel of VI term is a continuous function in time. Consider the V- FIE

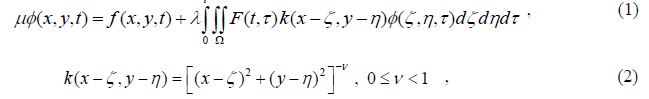in the space . Here, the kernel of position takes the form of generalized potential function and the kernel of VI term is a positive continuous function belongs to the classC[0,T ] . The free term f (x , y ,t ) is a known function, is the unknown potential function,  is the domain of position,  is called Poisson ratio, is a constant defines the kind of the IE, and  is a constant, may be complex, and has many physical meaning. In order to guarantee the existence of a unique solution of Eq. (1) we must assume the following conditions: (i) The discontinuous kernel in satisfies

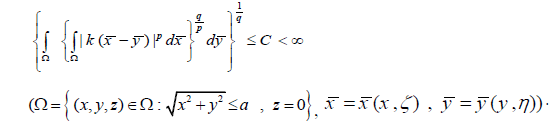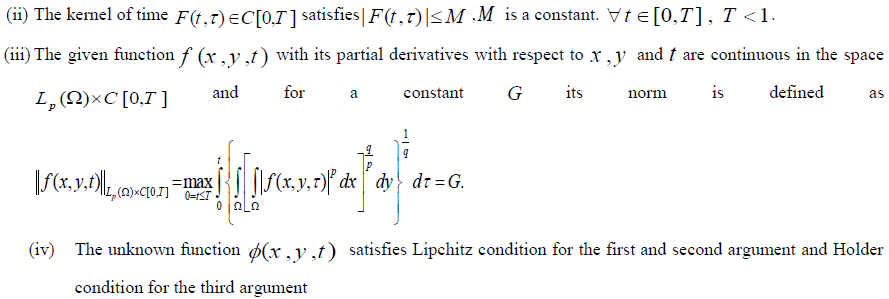Theorem (1) (without proof): The IE (1) has an existence and unique solution under the condition . In the reminder part of this work, we represent the generalized potential function in the form of Weber- Sonien integral formula (W-SIf). Then, we represent the W-SIf as a partial differential equation of the first order of Cauchy type. Moreover, the partial second derivatives are represented in the nonhomogeneous wave equation. 2. Weber-Sonien integral formula (W-SIf):

In this section, we represent the position kernel in the form of a generalized W-SIf. In this aim, after using the polar coordinates in Eqs. (1), (2), we obtain

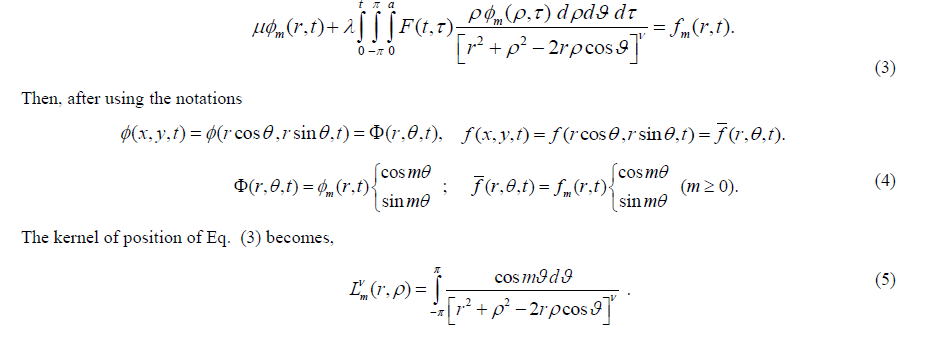Moreover, using the following three formulas, see Bateman and Ergyli [5, 6],

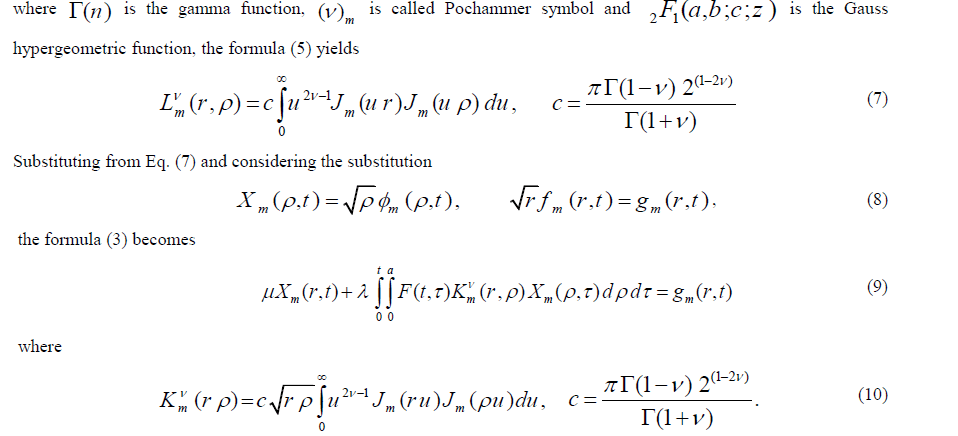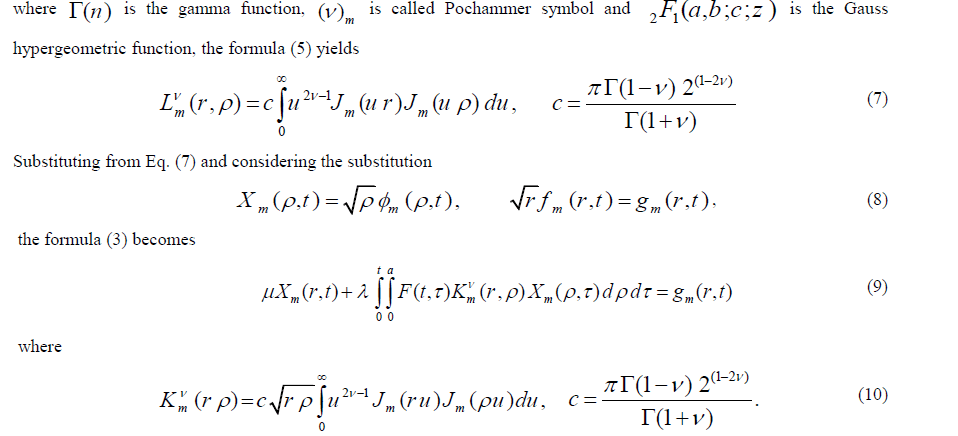The position kernel (10) takes a general form of W-SIf.

3. On the discussion of the W-SIf:

We derive many special and new cases from the W-SIf of (10)

(1) Logarithmic kernel: Let, in (10)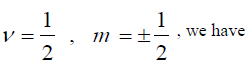

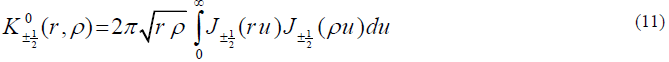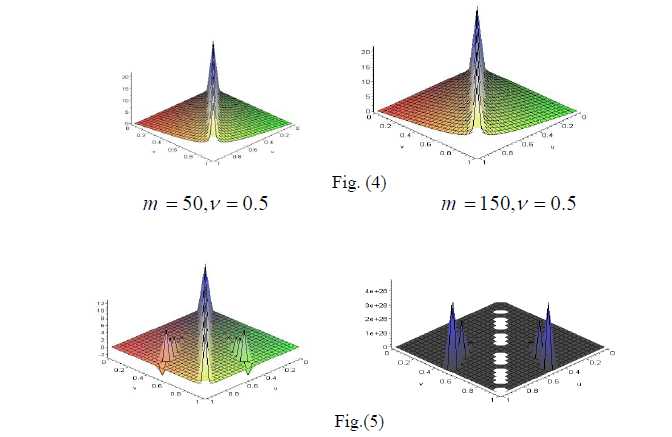
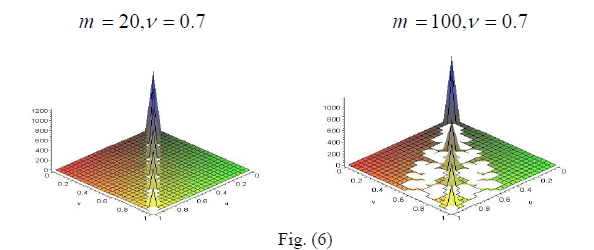
From the previous figures of Carleman function we deduced that as  increases the cracks in the material increase. (3) Elliptic kernel: Let, in (10), , we have the elliptic kernel. The importance of the elliptic kernel comes from the work of Kovalenko [7], who developed the FIE of the first kind for the mechanics mixed problem of continuous media and obtained an approximate solution of it.

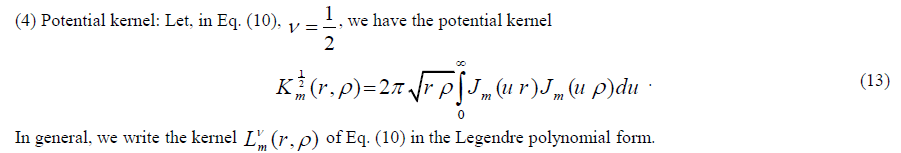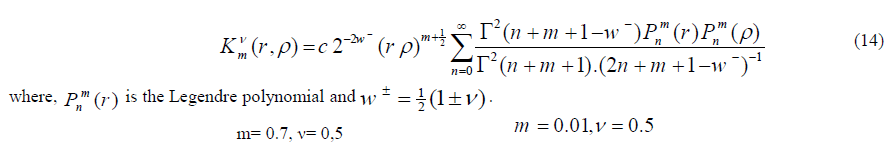General cases: Here, the W-SIf is representing generalized potential form , and as special cases we consider the following:

Theorem (2): The structure of the kernel W –SIf, represents Cauchy problem for the first order and nonhomogeneous wave equation for the second order. Proof: To prove this we differentiate Eq. (12) with respect to r and respectively, and then adding the result to get

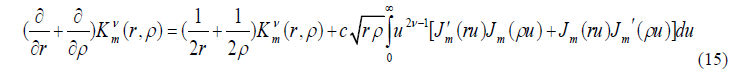Using the two famous relations, see Bateman and Ergelyi [6]

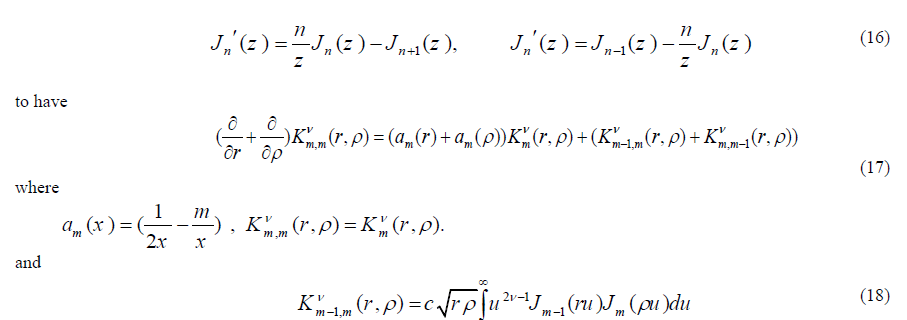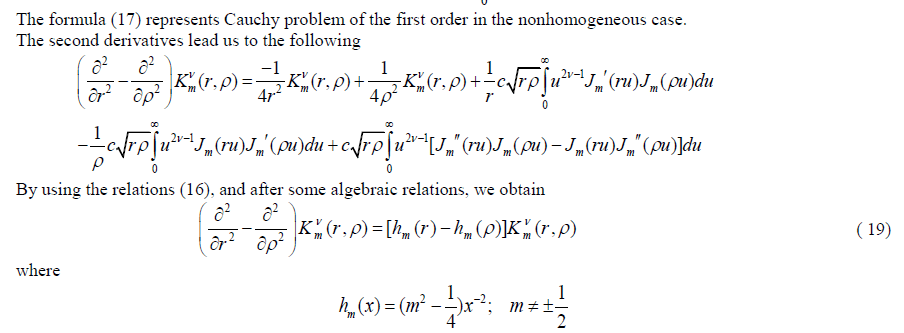The above formula represents a nonhomogeneous wave equation. So, the second derivative of the generalized potential kernel represents a nonhomogeneous wave equation when m≠0.5.

References

1. Abdou, M. A. " Associate Professor Fredholm-Volterra integral equation of the first kind and contact problem" J. Appl. Math. Comput. Vol. 125, pp 177-193, 2002.
2. Abdou, M. A. " Spectral relationships for the integral operators in contact problem of impressing stamp" J. Appl. Math. Comput. Vol. 118, pp. 95-111, 2001.
3. Abdou, M. A. "Spectral relationships for the integral equations with Macdonald kernel and contact problem" J. Appl. Math. Comput. Vol. 118, pp. 93-103, 2002.
4. Abdou, M. A. "Fredholm-Volterra integral equation and generalized potential kernel" J. Appl. Math. Comput. Vol. 131, pp. 81-94, 2002.
5. Bateman, G. and Ergelyi, A. "Higher Transcendental Functions" vol. 3 Mc-Graw Hill, London, New York, 1991.
6. Bateman, G. and Ergelyi, A. "Higher Transcendental Functions" vol. 2 Mc-Graw Hill, London, New York, 1989.
7. Kovalenko, E.V. "Some approximate methods of solving integral equations of mixed problems" J. Appl. Math. Mech. Vol. 53, pp. 85-192, 1989.