Generalized Version of the One-third Law

Abstract

While in the evolutionary game theory, the deterministic dynamics is mainly assumed, the stochastic dynamics as well as deterministic dynamics has been assumed in the recent several studies. A previous study developed a stochastic model of two-player games and specified the conditions required for natural selection to favor an invader eventually replacing the population consisting of the resident strategies in finite populations (Nowak et al.). It has been shown that the fixation probability of a single mutant in a population of resident strategies can be greater than 1/N, the fixation probability expected in the absence of natural selection, even when the resident strategy is ESS in the traditional sense. And Nowak et al. has derived the simple rule called the one-third law. Kurokawa and Ihara extended the two player games to n-player games and derived the {2/[n(n+1)]}1/(n–1) law (where n is the group size) as a generalized version of the one-third law. However, the {2/[n(n+1)]}1/(n–1) law holds true for some specific case, and when the law ({2/[n(n+1)]}1/(n–1) law) holds true is unexplored. This paper examines when the law ({2/[n(n+1)]}1/(n–1) law) holds true, and in addition, derives another extension of one-third law (1/[1+(n) 1/(n–1)] law).

Keywords

Evolutionary game theory, Stochastic process, The one-third law, Two player game, n-player game

Introduction

In the evolutionary game theory, the deterministic dynamics is mainly assumed [1,2]. However, stochastic dynamics has been focused on since Nowak, et al. [3] was published, and the stochastic dynamics as well as deterministic dynamics has been examined in the recent studies [3-18].

Nowak et al. [3] developed a stochastic model of two-player games and specified the conditions required for natural selection to favor an invader eventually replacing the population consisting of the resident strategies in finite populations. Assuming a discrete-time population of fixed size N with one individual replaced at a time according to the [3,19] Moran model, Nowak et al. showed that the fixation probability of a single mutant in a population of resident strategies can be greater than 1/N, the fixation probability expected in the absence of natural selection even when the resident strategy is ESS in the traditional sense. Furthermore, when both strategy A and strategy B are evolutionarily stable in the traditional sense (i.e., ESS), they demonstrated for sufficiently large population and for sufficiently weak selection that the fixation probability of A is larger than 1/N if p* < 1/3, where p* is the frequency of A at the unstable equilibrium in the conventional deterministic model (i.e., the one-third law).

Lessard, Imhof and Nowak [20,21] calculated the fixation probability on Wright-Fisher processes and showed that one-third law holds true on Wright-Fisher processes as well as on Moran processes. Lessard and Ladret [22] calculated the fixation probability on exchangeable processes including Moran processes and Wright-Fisher processes [23] and showed that one-third law holds true. Ohtsuki, et al. [24] investigated the meaning of one-third law. Hashimoto and Aihara [25] calculated the fixation probability in diploid populations and found ‘‘three-tenth law’’ and ‘‘two-fifth law’’ instead of “one-third law”.

Kurokawa and Ihara, Gokhale and Traulsen [4,8] extended the two player games to n-player games and obtained the fixation probabilities (with which a single mutant eventually replaces the population consisting of the resident strategies). And furthermore, Kurokawa and Ihara [4] have derived the {2/[n(n+1)]}^1/(n−1) law (, where n is the group size) as a generalized version of the one-third law.

However, the {2/[n(n + 1)]}^{1/(n – 1}) law holds true for the case where the iterated n-player prisoner’s dilemma is played by a reciprocator, which cooperates only when the every other n−1 group members cooperated in the previous round and an unconditional defector, and payoff is linear. And when the law ({2/[n(n + 1)]}^1/(n−1) law) holds true is not explored. In this paper, we examine when the law ({2/[n(n + 1)]}^1/(n−1) law) holds true. And furthermore, we derive another extension of one-third law.

Previous Studies [4,8]

Consider the situation where groups of n individuals are formed by randomly choosing individuals from a population, the size of which is N. And a game is played within each of these groups. We consider two strategies A and B, and payoff gained by each individual depends on its own strategy and the strategies of the other n−1 individual in the group. By aj, we denote payoff to an A individual when there are n – j other A individuals in the group, and by bj, we denote payoff to a B individual with n – j A individuals in the group, following [4] (Table 1). The expected payoffs of A and B individuals are described by

Table 1: The payoff matrix of the n-player game.

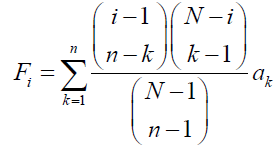(1)

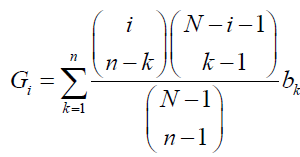(2)

Respectively, where i is the number of A individuals in the population (0 ≤ i ≤ N). Note that when l ≥ m is met, 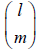represents a binomial coefficient and otherwise is defined as 0. The fitness of A and B individuals when there are i A individuals in the population are respectively given by

f_i = 1 − w + wF_i (3)

g_i = 1 − w + wG_i, (4)

where w is the selection intensity and specifies the contribution of the game to fitness [3]. Here, it is assumed that selection intensity is sufficiently weak (0 < w << 1). Population dynamics are formulated as a Moran process with frequency-dependent fitness. Concretely, at each time step, an individual is chosen for reproduction with the probability proportional to its fitness. And one identical offspring is produced to replace another individual randomly chosen for death with the probability 1/N [3,16]. In this process, there are two absorbing states, i = 0 and i = N. Kurokawa & Ihara and Gokhale & Traulsen [4,8] have shown, by using (1)- (4), that in the limit of large population size, the condition under which the fixation probability of A, ρ_A, with which a population at state i = 1 eventually reaches state i = N is over 1/N is given by

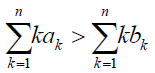(5)

Similarly, by using (1)-(4), the condition under which the fixation probability of B, ρ_B, with which a population at state i = N − 1 eventually reaches state i = 0 is over 1/N is given by

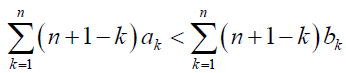(6)

It is also interesting to investigate whether A is more likely to replace B than vice versa. In the limit of large N, by using (1)- (4), it turns out that ρ_A is large than ρ_B if and only if

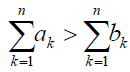(7)

In the RESULTS section, we assume that the population size is sufficiently large, and we use (5)-(7).

Results

Case 1:

In Case 1, we consider the case where a₁−b₁ is positive and a_k−b_k is constant for any k satisfying k>1 and negative. As defined in Introduction section, p* is the frequency of A at the unstable equilibrium in the conventional deterministic model.

By using (5), in our stochastic model, ρ_A > 1/N is equivalent to

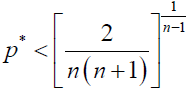(8)

Note that this inequality gives the {2/[n(n + 1)]}^{1/(n – 1}) law (a generalized version of the one-third law), obtained in Kurokawa and Ihara [4].

Similarly, by using (6), in our stochastic model, ρ_B > 1/N is equivalent to

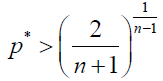(9)

Similarly, by using (7), ρ_A > ρ_B is equivalent to

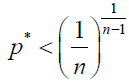(10)

Note that these inequalities give the (1/n) ^{1/(n – 1}) law (a generalized version of the one-half law), obtained in Ref [4].

Case 2:

In Case 2, we consider the case where a₁−b₁ is positive, and a_n−b_n is negative, and a_k−b_k=0 holds true for any k satisfying 1 < k<n. Note that this situation occurs if additional fitness is given to every player when and only when every player adopts the same strategy.

By using (5), in our stochastic model, ρ_A > 1/N is equivalent to

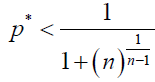(11)

Note that this inequality gives another generalized version of the one-third law, obtained in Ref [3].

Similarly, by using (6), in our stochastic model, ρ_B > 1/N is equivalent to

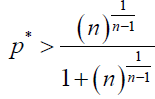(12)

Similarly, by using (7), ρ_A > ρ_B is equivalent to

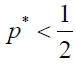
Note that these inequalities give the one-half law (a generalized version of the one-half law).

Conclusions

Stochastic dynamics as well as deterministic dynamics (such as replicator dynamics) is interesting. Nowak et al. [3] obtained the simple rule, called the one-third law. Kurokawa and Ihara [4] extended the one-third law and obtained the {2/[n(n + 1)]}^{1/(n – 1}) law; however, when this law holds true is not explored. This paper examined when the law ({2/[n(n + 1)]}^{1/(n – 1}) law) holds true and furthermore, we derive another extension of one-third law (1/[1 + (n) ^{1/(n – 1})] law).

Lessard [13] has revealed that (5)-(7) have been shown to hold also for an exchangeable model. Therefore, the findings in this paper are robust also for an exchangeable model.

Acknowledgements

This work was partially supported by Grant-in-Aid for JSPS Fellows and by Chinese Academy of Sciences President’s International Fellowship Initiative. Grant No. 2016PB018.

References

1. Maynard Smith J. Evolution and the theory of games. Cambridge University Press, Cambridge, UK; 1982.
2. Hofbauer J and Sigmund K. Evolutionary games and population dynamics. Cambridge University Press, Cambridge, UK; 1998.
3. Nowak MA, et al. Emergence of cooperation and evolutionary stability in finite populations. Nature 2004;428:646-650.
4. Kurokawa S and Ihara Y. Emergence of cooperation in public goods games. Proceedings of the Royal Society B 2009;276:1379-1384.
5. Kurokawa S and Ihara Y. Evolution of social behavior in finite populations: A payoff transformation in general n-player games and its implications. Theoretical Population Biology 2013;84:1-8.
6. Kurokawa S, et al. Generous cooperators can outperform non-generous cooperators when replacing a population of defectors. Theoretical Population Biology 2010;77:257-262.
7. Deng K, et al. Rare but severe concerted punishment that favors cooperation. Theoretical Population Biology 2012;81:284-291.
8. Gokhale CS and Traulsen A. Evolutionary games in the multiverse. Proceedings of the National Academy of Sciences of the United States of America 2010;107:5500-5504.
9. Zheng XD, et al. The diffusion approximation of stochastic evolutionary game dynamics: mean effective fixation time and the significance of the one-third law. Dynamic Games and Applications 2011; p: 462.
10. Wu B, et al. Extrapolating weak selection in evolutionary games. PLoS Computational Biology 2013;9:e1003381.
11. Wu B, et al. Fitness-based models and pairwise comparison models of evolutionary games are typically different-even in unstructured populations. New Journal of Physics 2015;17:023043.
12. Sekiguchi T and Ohtsuki H. Fixation probabilities of strategies for bimatrix games in finite populations. Dynamic Games and Applications 2015; pp: 1-19.
13. Lessard S. On the robustness of the extension of the one-third law of evolution to the multi-player game. Dynamic Games and Applications 2011;1:408-418.
14. Chalub FACC and Souza MO. Fixation in large populations: a continuous view of a discrete problem. Journal of mathematical biology 2016;72:283-330.
15. Zhang C and Chen Z. The public goods game with a new form of shared reward. Journal of Statistical Mechanics: Theory and Experiment 2016; p: 103201.
16. Moran PAP. Random processes in genetics. Mathematical Proceedings of the Cambridge Philosophical Society 1958;54:60-71.
17. Lessard S. Long-term stability from fixation probabilities in finite populations: new perspectives for ESS theory. Theoretical Population Biology 2005;68:19-27.
18. Imhof LA and Nowak MA. Evolutionary game dynamics in a Wright-Fisher process. Journal of mathematical biology 2006;52:667-681.
19. Lessard S and Ladret V. The probability of fixation of a single mutant in an exchangeable selection model. Journal of mathematical biology 2007;54:721-744.
20. Cannings C. The latent roots of certain Markov chains arising in genetics: a new approach. I. Haploid models. Advances in Applied Probability 1974;6:260-290.
21. Ohtsuki H, et al. The one-third law of evolutionary dynamics. Journal of Theoretical Biology 2007;249:289-295.
22. Hashimoto K and Aihara K. Fixation probabilities in evolutionary game dynamics with a two-strategy game in finite diploid populations. Journal of Theoretical Biology 2009;258:637-645.
23. Li X, et al. How life history can sway the fixation probability of mutants. Genetics 2016;203:1297-1313.
24. Liu X, et al. Aspiration promotes cooperation in the prisoner's dilemma game with the imitation rule. Physical Review E 2016;94:012124.
25. Peña J, et al. Evolutionary games of multiplayer cooperation on graphs. PLoS Computational Biology 2016;12:e1005059.