Hydrogen Permeation through Porous Stainless Steel for Palladium based Composite Porous Membranes

Abstract

Surface topography and hydrogen permeation properties of Porous Stainless Steel (PSS) substrates for thin–films deposition of Pd–based hydrogen separation membrane were investigated. Hydrogen permeance through the as–received PSS substrates demonstrated a wide range, despite a similar average surface pore size of 15 micron determined by SEM and confocal laser microscopy analyses. The surface pores of the PSS substrates were modified by impregnation of varying amounts of tungsten (W) powder. Maximum hydrogen flux reduction of only 28% suggested that W has a limited effect on the hydrogen permeation through the PSS substrate. Therefore, it is suggested that hydrogen transport through PSS substrates is mainly controlled by the substrate geometrical factors, particularly the ratio of the porosity to tortuosity (ε τ ). The variation in the permeance between the nominally similar PSS substrates indicates the importance to independently assess the hydrogen transport characteristics of each of the components in a composite membrane.

Keywords

Hydrogen separation, Palladium– based membrane, Porous stainless steel, Composite membrane, Surface modification.

Introduction

Dense palladium (Pd) metal offers excellent permeability for hydrogen, based on the solution–diffusion mechanism [1]. However, its application is limited due to the α to β phase transition during hydrogenation (at temperatures below 300ºC and pressures below 2 MPa), which involves a volume increase of 10% [2,3]. The change in volume leads to a lattice distortion, formation of high internal stresses, deformation, and ultimately failure of the membrane. The hydrogen embrittlement problem in combination with susceptibility of the pure Pd to surface poisoning by impurity gases [4,5] and the high cost of Pd have led to the exploration of a wide variety of Pd-alloy membranes [6-8].

Generally, Pd–Alloy foils with a thickness of 20–100 μm are required to provide acceptable levels of mechanical strength and produce a high purity hydrogen [1,9]. On the other hand, hydrogen flux is limited by the thickness of the membranes [10-12]. Furthermore, thick membranes are associated with higher costs and efforts continue to be made to reduce the material cost. One strategy to reduce the thickness and cost is to deposit a thin Pd or Pd–alloy film on the surface of porous substrate. This approach has been practiced extensively, where thin films of Pd or Pd–alloys were deposited on the porous substrate by various techniques such as electroless plating [13-20], sputtering [11,21-26], and chemical vapour deposition [27]. Non-metallic and metallic porous substrates such as ceramics [17,22,27-29], glass [21], and Porous Stainless Steel (PSS) [13,25,30-33] are widely employed. Although, the smooth surfaces provided by ceramic and glass porous substrates can be conducive to thin–film deposition, the relatively poor adhesion of the fabricated metal film to the substrates [8] limits the application of these substrates. In fact, failure of Pd or Pd–alloy films during thermal cycling and hydrogen loading was attributed to the rising shear stresses as a result of the different elongations of metallic layer and ceramic support at the interface [34]. The scale of such a shear stress was shown to be directly related to the thickness of the metallic film and therefore, thermal stability with a lower thickness of metallic film can be achieved only in the expense of reduced hydrogen selectivity.

Alternatively, PSS can be a suitable support for Pd or Pd–alloys film deposition because of the low cost, mechanical durability, and its close coefficient of thermal expansion to Pd (1.73×10^-5 and 1.17×10^-5 for 316L stainless steel and Pd respectively). However, because of the rough surface and a wide distribution range of the surface pore size, depositing a thin and pinhole free film becomes challenging. The effect of the surface smoothness of the PSS support on the deposited Pd film was investigated by Mardilovich [10]. It was shown that the surface of the PSS support greatly influence the final topology of the deposited film. This result further confirmed the initial work by Ma. [35] indicating the thickness of the deposited film requires to be at least three times higher than the maximum surface pore size to achieve a dense Pd film. In addition, solid state inter–diffusion at higher temperatures than Tamman temperature of stainless steel (550 oC) leads to the alloying of PSS with Pd, causing degradation of hydrogen permeability with time [8,36]. Combination of these problems highlights the requirement for the surface modification of PSS substrate before the thin–film deposition. The common method to modify the surface of the PSS is to use an intermediate layer capable of reducing the surface pore size whilst, simultaneously serving as an inter–diffusion barrier. Various intermediate layers such as Al₂O₃ (alumina) [16,30], TiN [36], ZrO₂ [31], Ni [14], W/WO₃ [37,38], and Yttria-Stabilised Zirconia (YSZ) [12,39] have been employed. In addition, Ma et al. [40] investigated the formation of an in-situ oxide layer on the surface of PSS as an inter–diffusion barrier. Oxide layer formed at 800ºC showed to be effective for forming a membrane with an effective inter–metallic diffusion barrier. However, further studies [41] showed that PSS substrate with in-situ oxide layer has a rougher surface in comparison with YSZ modified PSS substrate and therefore, it requires a larger thickness of Pd layer and has a larger permeation resistance. Other intermediate layers, such as Ag [42], and Pd–Ag [15] have been also shown to serve as an effective barrier for the diffusion of iron to the palladium layer. However, electroplating of a thin layer of Ag on PSS required a subsequent treatment with aluminium hydroxide gel to insure the evenness of the surface for the final Pd layer deposition. In contrast, Bi-Metal Multi-Layer electroless deposition (BMML) of the Pd–Ag as an intermediate layer formed a graded support without significantly changing the resistance of the PSS support, suitable for the final Pd layer deposition. Furthermore, Li et al. [43] modified PSS substrate by two layers of alumina with varying sizes and showed only a mild reduction in the permeability of hydrogen and nitrogen through the membrane at ambient temperature. Whilst, there are ample of reports investigating the surface pore size modification by intermediate layers and their effectiveness as an inter–diffusion barrier, less attention has been paid to the gas permeability of PSS substrate itself and its relation to the surface modification. Here, surface topography and hydrogen permeation through the as received PSS substrates are investigated. PSS substrates are then modified by impregnating with sub–micron tungsten into surface pores. The extent of pore filling and the corresponding hydrogen permeation properties through the tungsten modified PSS are investigated and the main controlling factors for the hydrogen permeation through PSS are discussed.

Materials and Methods

Porous sintered austenitic 316L Stainless Steel (PSS) substrate discs were purchased from Mott Metallurgical Corporation. The PSS discs had a diameter of 21 mm, thickness of 1 mm and a media filtration grade of 0.1 μm. The filtration grade is calculated and defined as the minimum size of a hard spherical particle retained by the interconnected porosity [44], with 0.1 being the finest commercially available grade. All discs were cleaned with acetone in an ultrasonic bath for 15 min and dried thoroughly using a heat gun prior to use. Tungsten powder with sub–micron particles was purchased from Sigma–Aldrich. 0.1 g tungsten powder was dispersed in in 10 ml Industrial Methylated Spirits (IMS) to facilitate the coating of the PSS surface. A vacuum was applied to the underside of the PSS substrate and an even layer of tungsten powder was impregnated onto the surface (denoted as 1 layer). The tungsten coating process was repeated three times for some selected samples to triple the amount of the impregnated tungsten (denoted as 3 layers). Tungsten coated discs were then wrapped in stainless steel foil and heat treated at 900oC for 2 h under vacuum of approximately 10^-4 mbar.

Stainless steel target (99.9% purity) was obtained from Teer Coatings Ltd. Films of 316 Stainless Steel (SS) of 5–20 μm thickness were deposited onto the as–received substrates using a Closed Field Unbalanced Magnetron Sputter Ion Plating (CFUBMSIP) system supplied by Teer Coatings Ltd. The sputtering chamber was evacuated to approximately 10^-6 mbar prior to the depositions and refilled to ~ 2.5×10^-3 mbar with continuous flow (25 ml/min) of ultra–high purity argon during the deposition runs. A bias voltage of 50 volts was applied to the magnetron during deposition runs. Samples were deposited using pulsed DC, with a constant target to substrate distance and a sample rotation speed of 8 rpm. A target currents of 2 (A) was applied for the stainless steel coatings.

Surface morphologies were examined by a Joel 6060 Scanning Electron Microscopy (SEM) equipped with an INCA 300 Energy Dispersive Spectroscopy (EDS). The surface roughness, and pore size were also further investigated by the Olympus LEXT OLS 3100 mounted on a TableStable anti–vibration table. The system uses a 408 nm Class II ultraviolet laser source and has a plane resolution (X and Y) of 120 nm and a space pattern (Z resolution) of 10 nm.

Hydrogen flux was measured using a hydrogen permeation system designed and built in the School of Metallurgy and Materials Science at the University of Birmingham [45]. The system was de-gassed under 10^-5 mbar vacuum prior to hydrogen (99.99995%, BOC) admittance. The feed gas was controlled using Brooks 5850S Mass Flow Controller (MFC) calibrated over a range of 6–600 ml min^-1 with an accuracy of ±6 ml min^-1. A constant upstream pressure was applied by continuous hydrogen flow and bled using another Brooks 5850S MFC. The permeated gas flow was measured by Brooks 5850S MFC placed on the low pressure side. To establish a gas tight seal, copper gaskets were used on each side of the sample.

Results and Discussion

As–received PSS Substrate

The surface topography of the as-received PSS substrate is shown in Figure 1a. Whilst SEM images suggest an average diameter of approximately 15 μm for the surface pores, further analyses of the 3–Dimensional images obtained by confocal laser microscope (Figure 1b) showed the both surface pore diameter and the pore depth ranged between 10 to 25 μm in a good agreement with the previously reported values by Li et al. [43]. Also, the average density was determined to be 6.34 g cm-3 indicating an overall volume porosity of approximately 20% compared to fully dense 316L dense stainless steel [46]. To investigate the suitability of the as–received PSS substrate for thin–film deposition, thin–films of stainless steel with varying thicknesses from 5–20 μm were deposited onto the surface of PSS substrates. However, the SEM image in Figure 1c, in conjunction with the confocal laser microscopy image in Figure 1d, indicates that a continuous stainless steel film cannot be achieved even after depositing a 20 μm film. Based on the minimum requirement thickness rule proposed by Ma et al. [34], for the as-received PSS with an average surface pore size of ~ 15 μm, depositing a layer of approximately 45 μm is required to achieve a continuous and defect free layer. Hence, depositing a thin–film of Pd or Pd–alloys on the surface of the as–received PSS seems to be impractical and surface modification is required to achieve a smaller surface pore size.

Figure 1: SEM image of the surface topography of as-received PSS substrate (a), and the corresponding confocal laser image with line profile (b). SEM image of the surface topography of PSS substrate coated with 20 μm stainless steel (c), and the corresponding confocal laser image with line profile (d). Line profile scale is in micron.

Surface Modification with Tungsten

Surface modification of the PSS was performed by impregnating sub–micron tungsten powder on to the surface of the PSS. Figure 2a, shows the surface of the PSS substrate modified by impregnating of 1 layer of tungsten powder. An even coverage of the PSS surface is observed indicating tungsten can effectively modify the surface by filling the pores. The line profile in Figure 2b suggests almost 50% reduction in depth of the surface pores as a result of tungsten modification in comparison to the as– received PSS substrate (Figure 1b). However, the extent of the pore filling seems to be insufficient as it can be seen in Figure 2b and the corresponding line profile shows that pores are not filled equally. Consequently, the surface of the PSS was modified by tripling the amount of tungsten (3 layers) in Figure 2c. The extent of the pore filling was examined by confocal laser microscope in Figure 2d. The line profile shows that the surface pores of the PSS have been effectively filled. However, Figure 2c also shows that tungsten powder is residing on the PSS surface as its quantity increases (3 layers), leading to a higher surface roughness. This is shown in the line profile image of the PSS sample modified by 3 layers of tungsten (Figure 2d), where the pores seem to be overfilled and tungsten clusters are formed on the surface. The scale of the tungsten clusters represents a rough uneven surface, which can deter the formation of a continuous and defect free thin–film. Therefore, in order to deposit continuous thin–films with less than 5 μm thickness, surface modification method needs to be controlled precisely by a sufficient amount of tungsten powder to maximise the surface pore filling, whilst minimizing the formation of powder clusters on the surface.

Figure 2: SEM image of the surface topography of PSS substrate modifed by 1 layer of submicron tungsten powder (a), and the corresponding confocal laser image with line profile (b). SEM image of the surface topography of PSS substrate modifed by 3 layers of submicron tungsten powder (c), and the corresponding confocal laser image with line profile (d). Line profile scale is in micron.

Hydrogen Permeation

In general, the transport mechanism of a molecular gas through a porous medium is a complex combination of viscous (Poiseuille) flow, slip flow, Knudsen diffusion and continuum binary diffusion [45,47]. It is also known that viscous flow and Knudsen diffusion are the preferred transport mechanism through macroporous membranes or supports having a pore size greater than 1.5 nm [48,49]. As described in Section 3.1, the average surface pore size of the as-received PSS discs is about 15 μm. Therefore, the total gas transport across the PSS substrate can be expressed by viscous flow and Knudsen diffusion mechanisms. The relative contribution of each transport mechanism can be established by a characteristic parameter, i.e. Knudsen number (K_n). Knudsen number is defined by K_n= λ/r, that is the ratio of the average free path of the gas molecules (λ) over the mean pore radius (r) [45,49]. When the pore size is smaller than the average free path, the Knudsen number becomes much larger than unity (K_n>>1). This is a condition under which gas molecules travel independently from each other and the number of molecule-wall collisions becomes strongly dominant. Under this condition the hydrogen flux (J_K) can be described by Knudsen equation (equation 1) [45]

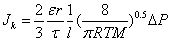(1)

Where ε is the porosity, r the average pore radius, τ the tortuosity, M the molecular mass, and R, T, l, and ΔP denote the gas constant, absolute temperature, substrate thickness and the pressure differential across the membrane. On the other hand, when the pore size is bigger than the average free path (K_n<<1), the number of intermolecular collisions is strongly dominant giving predominantly laminar Poiseuille flow. The hydrogen flux (J_v) follows the Hagan-Poiseuille law given in equation (2) [45].

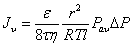(2)

where Pav is the average pressure across the substrate and η denotes fluid viscosity. Because viscous and diffusive transport mechanisms are completely independent from each other [47], the overall hydrogen flux through the PSS substrate is a sum of the viscous flow and Knudsen diffusion (equation 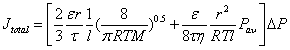3).

(3)

Using the assumption of linear pressure drop across the membrane [49], equation (3) can be simplified to:

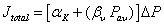eq (4)

Where α_K is β_V are the average Knudsen and Poiseuille permeation coefficients respectively. α_K and β_V can be calculated by plotting total flux 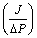((mol m^-2 s^-1 Pa^-1) versus average pressure (Pa) determined from experimental measurements. α_K and β_V coefficients allows the calculation of the average geometrical factors 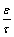it is difficult to isolate either the porosity or the tortuosity uniquely, as a result they are usually reported as 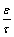ratio) and average r of the substrate as well as prediction of the gas flux under any conditions of both temperature and pressure [45]. Initially, hydrogen permeability of 16 as-received PSS samples was measured at room temperature. All samples were taken from the same commercial batch, exhibiting similar average surface pore size. Surprisingly, the hydrogen permeance through the samples varied widely, despite their similar average surface pore size. Figure 3, shows variation of hydrogen permeance against the average pressure for some selected PSS samples, where sample (16) and (11) represent upper and lower extremes respectively. α_K and β_V coefficients of each sample is displayed within the Figure 3. Comparisons between α_K and β_V values of samples (16) and (11), reveal that whilst sample (16) has slightly lower α_K value, its β_V value is almost doubled. The overall variation in the measured coefficients leads to the hydrogen flux for sample (16) being more than 1.5 times greater than that of sample (11) at the final point of measurement (Figure 4). From equation 3, it can be seen that variations in the hydrogen flux for different samples arises from the contribution of the geometrical factors ε, τ, and r for the overall hydrogen flux through the PSS substrate. To further investigate the effect of geometrical factors, values of r and 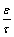ratio were calculated from the experimentally determined α_K and β_V coefficients for some selected samples in Table 1. It is evident that the average pore size values derived from gas flow analysis, listed in the Table 1, are significantly smaller than the average externally observed surface pore size (~15 μm). Interestingly, whilst sample (10) represents the largest calculated pore size, it does not possess the largest hydrogen flux. This phenomenon can be in fact explained by the calculated 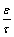ratio. Whilst, porosity in equation 3 is defined as the fraction of the open media in any particular plane, tortuosity refers to an increased distance a gas molecule must travel in comparison to the substrate thickness [45]. The largest hydrogen flux belongs to the sample (7), which represents the biggest 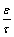ratio (Table 1). However, it can be seen that sample (7) has much smaller calculated average pore size in comparison with sample (10). Therefore, it seems that the hydrogen flux through the sample (10) is limited by internal structure of the sample. In addition, hydrogen flux through the tungsten modified PSS substrates was investigated for some selected samples modified by either 1 or 3 layers of tungsten (Figure 4). Whilst, the hydrogen flux reduction in comparison with the as-received PSS substrate ranged from 8% to 11% for the samples modified by 1 layer of tungsten, a higher hydrogen flux reduction between 20 to 28% was observed for the samples modified by 3 layers of tungsten. Although, an increase in the amount of tungsten enhanced the hydrogen flux reduction, the maximum flux reduction of 28% observed for the sample (5) suggests that tungsten does not have a dominant effect in altering the hydrogen flux through the surface porosity of the PSS substrate. This result also suggests that geometrical factors are the limiting feature that dominate the hydrogen permeability through the PSS substrate. A wide range of hydrogen flux observed for the different PSS substrates from the same batch of samples indicates that the substrate resistance can significantly vary for each PSS composite membrane. Hence, the substrate resistance needs to be accounted to correctly determine the hydrogen permeability through the deposited thin–film. Therefore, further investigations into the composite membranes should be focused in developing more suitable PSS substrates in order to minimise the hydrogen permeability resistance induced by geometrical factor and increasing the surface pore density whilst retaining the necessary pore dimension required for the deposition of the defect–free film.

Figure 3: Variation in the room temperature hydrogen permeance through some selected as-received PSS substrates including α_K and β_V coefficients of each sample.

Figure 4: Comparison of the room temperature hydrogen flux for selected samples before and after the modification with (a) 1 layer and (b) 3 layers of tungsten powder.

Sample	Flux(mol m-2 s-1)	αK(mol m-2 s-1 Pa-1)	βV(mol m-2 s-1 Pa-2)	r(micron)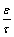
Sample (4)	1.473	8.54×10-6	1.42×10-10	0.45	1.127
Sample (7)	1.782	1.31×10-5	1.51×10-10	0.30	2.897
Sample (10)	1.659	5.59×10-6	1.87×10-10	0.87	0.424
Sample (11)	1.165	9.68×10-6	9.11×10-11	0.24	2.602

Table 1. Comparison of the room temperature hydrogen permeance coefficients and the average geometrical factors in as-received PSS substrates. Hydrogen flux measured at 1 bar pressure differential.

Conclusions

Porous Stainless Steel as a substrate for thin–film composite porous membranes was investigated. Surface analyses of the PSS substrates, with the filtration grade of 0.1 μm, by SEM and confocal microscopy suggested an average surface pore size of approximately 15 μm. The as–received PSS substrate was not suitable for the deposition of continuous thin–films even when coated with 20 μm of Stainless steel. Hence, surface porosity of the PSS substrates was modified by impregnating with submicron tungsten powder. It was noticed that whilst an increase in the amount of tungsten powder improves the extent of the pore filling, it can also increase the surface roughness by the formation of powder clusters on the surface. Therefore, in order to deposit a continuous thin–film of less than 5 μm in thickness, the present work indicates that precise control of the amount of tungsten powder is required to minimise the formation of powder clusters on the surface whilst maximising the extent of the pore filling. Hydrogen transport through the selected as–received PSS samples was suggested to be a combination of the Knudsen diffusion and Poiseuille flow. Notable discrepancies in the hydrogen flux through the as–received substrates were observed, despite their similar average surface pore size, A maximum flux reduction of 28%, which was observed after the surface modification of PSS substrates by tungsten, indicates the capability of tungsten to physically modify the surface without significantly reducing the hydrogen flux through the substrate. Therefore, a significant contribution of the geometrical factors i.e. 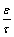ratio on the overall hydrogen flux through the nominally similar PSS substrate is suggested.

Acknowledgements

Support from the EPSRC SUPERGEN Delivery of Sustainable Hydrogen (EP/G01244X/1), the Birmingham Science City Hydrogen Energy projects, and the Hydrogen and Fuel Cell Research Hub, is gratefully acknowledged.

References

1. Dittmeyer R, et al.Membrane reactors for hydrogenation and dehydrogenation processes based onsupported palladium. Journal of Molecualr CatalysisA: Chemical. 2001;173:135
2. Alefeld G andVölkl J.Hydrogen in metals II: Application-oriented properties. Springer-Verlag, Berlin 1978.
3. Knapton AG.Palladium alloys for hydrogen diffusion membranes. Platinum Metals Review. 1977;21:2-44.
4. Morreale BD, et al.Experimental and computational prediction of the hydrogen transport properties of Pd4S. Industrial & Engineering Chemistry Research.2007;46:6313
5. Khatib SJ.Sulfur resistant Pd and Pd alloy membranes by phosphidation.Journal of Membrane science.2014;455:283
6. Grashoff GJ,et al.The purification of hydrogen: a review of the technology emphasizing the current status of palladium membrane diffusion. Platinum Metals Review. 1983;27:4-157
7. Adhikari S and Fernando S, Hydrogen membrane separation techniques. Industrial & Engineering Chemistry Research. 2006;45:875
8. BasileA et al. Synthesis, characterisation, and application of palladium membranes. Membrane Science and Technology. 2008;13:255
9. Yun S and Oyama ST. Correlation in pallasium membranes for hydrogen sepration: a review. Journal of Memebrane Science. 2011;375:28
10. Mardilovich IP, et al.Dependence of hydrogen flux on the pore size and plating surface topology of asymmetric Pd-porous stianless steel membranes. Desalination.2002;144:85
11. Yang JY,et al. Effect of overlayer thickness on hydrogen permeation of Pd60Cu40/V-15Nicompositemembranes. International Journal of Hydrogen Energy.2007;32:1820
12. Hatlevik SK, et al.Palldium and palldium alloy membranes for hydrogen separation and production: history, fabrication strategies and current performance. Separation and Purification Technology. 2010;73:59
13. Li A, et al. Characterisation and permaeation of palladium/stainless steel composite membranes. Journal of Membrane Science. 1998;149:259
14. Nam SE, et al.Prepration of palldium alloy composite membrane supported in a porous stianless steel by vacuum electrodeposition. Journal of Membrane Science. 1999;153:163
15. Ayturk ME et al.Synthesis of composite Pd-porous stainless steeel (PSS) membranes with a Pd/Ag intermetallic diffusion barrier. Journal of Membrane Science.2006;285:385
16. Bosko ML, et al.Surface, Characterisation od Pd-Ag composite membranes after annealing at various temperatures. Journal of Membrane Science. 2011;369:267.
17. David E and Kopac J.Development of palldium/ceramic membranes for hydrogen speration. International Journal of Hydrogen Energy. 2012;36:4498
18. Zhang D, et al.Prepration of dense Pd composite membrnaes on porous Ti-Al alloy supports by electroless platting. Journal of Membrane Science.2012;24:387-388
19. Islam MS,et al. Characterization of Pd-Cu membranes fabricated by surfactant induced electroless platting (SIEP) for hydrogen separation.International Journal of Hydrogen Energy. 2012;37:3477
20. Kim SS,et al.Development of a new Porous metal support based on nickel and its application for Pd based composite membranes. International Journal of Hydrogen Energy.2015:40:3520
21. Bryden KJ andYing JY.Nanostructured palladium membrane synthesised by magnetron sputtering. Materials Science and Engineering.1995;204:140
22. McCool BA and LIN YS.Nanostructured thin palladium–silver membrnaes: effects of grain size on gas permeation properties. Journal of Mateirals Science.  2001;36:3221.
23. Hoang HT, et al.Fabrication and chracterisation of dual sputtered Pd-Cu alloys films for hydrogen separation membranes. Materials Letters. 2004;58:525
24. Yang JY, et al. Prepration and characterisation of Pd-Cu/V-15Ni composite membrane for hydrogen permeation. Journal of Alloys and Compounds. 2007;431:180.
25. Petters TA, et al.Thin Pd-23%Ag/stainless steel composite membranes: Long-term stability, life-time estimation and post-process characterisation.Journal of Memebrane Science. 2009;326:572.
26. Ryi SK, et al.Pd-Cu alloy membrane deposited on alumina modified porous nickel support (PNS) for hydrogen separation at high pressure. Korean Journal of Chemical Engieering. 2012;29:59.
27. Xomeritakis G and Lin YS.Fabrication of thin metallic membranes by MOCVD and sputtering. Journal of Membrane Science. 1997;133:217.
28. Roa F, et al. The influence of aloy composition on the H2 flux of composite Pd-Cu membranes. Desalination. 2002;147:411.
29. Li Y, et al.Toward extensive application of Pd/ceramic membranes for hydrogen separation : A case study on membrane recycling and reuse in the fabrication of new membranes. International Journal of Hydrogen Energy. 2015;40:528.
30. Li A, et al.Prepration of thin Pd-based composite membrane on palanar metallic substrate. Part II: prepration of membranes by electroless platting and chracterisation. Jounral of Membrane Science. 2007;06:159
31. Gao H,et al.Electroless platting synthesis, characterisation and permeation properties of Pd-Cu membranes supported on ZrO₂ modified porous stainless steel. Journal of Membrane Science.2005;265:142.
32. Ryi Sk,et al.Electroless plating of Pd after shielding the bottom of planar porous stainless steel for a highly stable hydrogen selective membrane. Journal of Membrane Science. 2014;467:93.
33. Wei L, et al. Aluminizing and oxidation treatments on the porous stainless steel substrate for preparation of H2–permeable composite palladium membranes. International Journal of Hydrogen Energy. 2014;39:18618
34. Tosti S,et al. Sputtered,electroless,and rolled palladium-ceramic membranes. Journal of Membrane Science. 2002;196:241.
35. Ma YH.Effects of porosity and pore size distribution of the porous stainless steel on the thickness and hydrgeon flux of palladium membranes. Journal of American Chemical Society.2001;46:2
36. Shu J,et al.Structurally stable composite Pd-Ag alloy membranes: introduction of a diffusion barrier. Thin Solid Films. 1996;286:72.
37. Gryaznov VM,et al.Prepration and catalysis over palldium composite memebrane. Applied Catalysis A. 1993;96:15
38. Zahedi M.Prepration of a Pd membrane on a WO₃ modified porous stainless steel for hydrogen separation.Journal of Membrane Science. 2009;333:45.
39. Huang Yand Dittmeyer R.Prepration of thin palladium membranes on a porous support with rough surface. Journal of Memebrane Science. 2007;302:160
40. Ma YH, et al.Characterisation of intermetallic diffusion barrier and alloy formation for Pd/Cu and Pd/Ag porois stainless steel composite membranes. Industrial & Engineering Chemistry Research.2004;43:2936
41. Zhang K, et al.High Temperature stability of palladium membranes on porous metal supports with different intermediate layers. Industrial & Engineering Chemistry Research. 2009;48;1880.
42. Tong J,et al.Prepration of a pinhole-free Pd-Ag membrane on a porous metal support for pure hydrogen separation. Journal of Memebrane Science. 2005;260:84.
43. Li A, et al.Prepration of thin Pd-based composite membrane on planar metallic substrate, Part I: pre-treatment of porous stainless steel substrate. Journal of Membrane Science. 2007;298:175.
44. Guidebook, Mottcorp 2.S.
45. Fletcher. Thin-film palladium-yttrium membranes for hydrogen separation.2009 316/316L product data sheet. AK steel Corporation 2007.
46. Beuscher U and Goodings CH. The permeation of binary gas mixtures through support structures of composite membranes. Journal of Membrane Science.1998;150:57.
47. Uhlhorn RJR, et al.Gas and surface diffusion in modified γ-alumina systems. Journal of Membrane Science. 1989;46:225.
48. Gabitto J andTsouris C.Hydrogen transport in composite inorganic membranes. Journal of Membrane Science.2008:312:132.
49. Burggraaf AJ.Transport and separation properties of membranes with gases and vapours fundamental of inorganic membrane science and technology.1996