ISSN ONLINE(2320-9801) PRINT (2320-9798)
ISSN ONLINE(2320-9801) PRINT (2320-9798)
C.Gnana Prakash1, K.Shanthi2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering
A distributed scheme to detect if a node has debased its rate limits. To address the challenge that it is difficult to count all the packets or replicas sent by a node due to lack of statement infrastructure, our detection adopts claim-carry-and check: each node itself counts the number of packets or replicas that it has sent and claims the count to other nodes; the getting nodes carry the claims when they move, and cross-check if their carried claims are inconsistent when they contact. The claim structure uses the pigeonhole standard to guarantee that an attacker will make conflicting claims which may lead to discovery. We present rigorous analysis on the probability of detection, and assess the effectiveness and efficiency of our scheme with extensive trace driven simulations. Using Lyapunov optimization, we extend this examination to design a utility Maximizing algorithm that uses explicit delay information from the head-ofline packet at each user. The consequential policy is shown to ensure deterministic worst-case delay guarantees and to yield a throughput utility that differs from the optimally fair value by an amount that is inversely proportional to the delay guarantee. Our results hold for a general class of 1-hop networks, including packet switches and multiuser wireless systems with time varying reliability.
Keywords |
| Lyapunov optimization, claim-carry-and check, 1-hop networks, packet switches. |
INTRODUCTION |
| In this paper, we employ rate limiting [15] to defend beside flood attacks in DTNs. In our approach, each node has a limit over the number of packets that it, as a source node, can send to the network in each time interval. Each node also has a boundary over the numeral of replicas that it can generate for each packet (i.e., the number of nodes that it can forward each packet to). The two limits are used to mitigate packet flood and model flood attacks, respectively. If a node violates its rate limits, it will be detected and its data traffic will be filtered. In this way, the amount of flooded traffic can be controlled. |
| Our main role is a procedure to notice if a node has violated its rate limits. Although it is easy to detect the violation of rate limit on the Internet and in telecommunication networks where the egress router and base station can account each user’s traffic, it is challenging in DTNs due to lack of communication infrastructure and consistent connectivity. Since a node moves approximately and may send data to any contacted node, it is very difficult to count the number of packets or replicas sent out by this node. Our essential idea of detection is claim-carry-and-check. Each node itself counts the number of packets or replicas that it has sent out, and claims the count to other nodes; the receiving nodes carry the claims around when they move, swap some claims when they contact, and cross-check if these claims are inconsistent. If an attacker floods more packets or replicas than its limit, it has to use the same calculate in more than one claim according to the pigeonhole principle, and this inconsistency may lead to detection. Based on this idea, we use different cryptographic constructions to detect packet flood and replica flood attacks. |
| Because the contacts in DTNs are opportunistic in nature, our approach provides probabilistic detection. The more traffic an attacker floods, the more likely it will be detected. The detection probability can be flexibly adjusted by system parameters that control the amount of claims exchanged in a contact. We provide a inferior and better bound of detection probability and examine the problem of parameter selection to maximize detection probability under a certain amount of exchanged claims. The effectiveness and efficiency of our scheme are evaluated with extensive trace-driven simulations. This paper fills that gap. We use a delay-based Lyapunov function and extend the examination to treat joint stability and presentation optimizat ion via the Lyapunov optimization technique from our prior work [2], [13], [14]. The extension is not obvious. Indeed, the flow control decisions in the prior work [2], [13], [14] are made immediately when a new packet arrives, which directly affects the drift of backlog-based Lyapunov functions. However, such decisions do not directly affect the delay value of the head-of-line packets, and hence do not directly affect the drift of delay-based Lyapunov functions. We overcome this challenge with a novel flow control policy that queues all arriving data, but makes packet dropping decisions just before advancing a new packet to the head-of-line. This policy is structurally different from the service optimization works [2] and [13]–[20]. This new structure leads to deterministic guarantees on the worst-case delay of any nondropped packet and provides throughput utility that can be pushed arbitrarily close to optimal. Specifically, for any integer we Similar performance tradeoffs are shown for queue-based Lyapunov functions in the previous work [2], [13], [14] (see also [24]–[26] for improved tradeoffs), but these guarantees apply only to queue size, slightly than delay. |
| The deterministic delay guarantees we obtain in this present paper are quite strong and show the advantages of our new flow control structure. However, a disadvantage is that admit/drop decisions are delayed until a packet is at the head-ofline, rather than being determined immediately upon arrival. Moreover, due to correlation issues unique to this delaybased scenario, analysis is simplified if we assume the scheduler knows the vector of arrival rates to each link (although we also generalize to cases when these rates are unknown). Furthermore, while our deterministic delay guarantees hold for general arrival sample paths, our utility analysis assumes all entrance processes are independent of each other (possibly with different rates for each process) and independent and identically distributed (i.i.d.) over time-slots. Nevertheless, it is important to analyze these delay-based policies because they improve our understanding of complex delay, and because the deterministic guarantees they offer are useful for many practical systems. |
| We further show via simulation that our algorithms maintain good performance when the i.i.d. arrivals are replaced by ergodic but temporally correlated “bursty” arrivals with the same rates. However, the worst-case delay required to achieve the same utility performance is amplified in this case. This is not surprising if we compare to known results for backlog-based Lyapunov algorithms. Backlog-based algorithms were first developed under i.i.d. assumptions, but later shown to work—with increased delay—for non-i.i.d. cases (see [28] and references therein). Thus, while we limit our analytical proofs to the i.i.d. setting, we expect the algorithm to approach optimal utility in more general cases, as supported by our simulations. While our algorithm can be used to enforce any desired delay guarantee, it is important to emphasize that it does not maximize throughput utility subject to this guarantee. Such a problem can be addressed with Markov decision theory, which brings with it the curse of dimensionality (see structural results and approximations in [29] and weighted stochastic shortest-path approaches in [30]). proaches in [30]). In this paper, we claim only that the achieved utility is within of the largest probable utility of any stabilizing algorithm. However, because (for large ) our utility is close to this ideal utility value, it is even closer to the maximum utility that can be achieved subject to the worst-case delay constraint. That is because a basic stability constraint is less stringent than a worst-case delay constraint, and so the optimal utility under a stability constraint is greater than or equal to the optimal utility under a worst-case delay constraint. Furthermore, our approach offers the low-complexity advantages associated with Lyapunov drift and Lyapunov optimization. Specifically, the policy makes real-time broadcast decisions based only on the current system state and does not require apriori knowledge of the channel-state probabilities. The flow control decisions here can also be implemented in a distributed fashion at each link, as is the case with most other Lyapunovbased utility optimization algorithms. |
II. OVERVIEW |
2.1 Problem Definition |
Defense against Packet Flood Attacks |
| We consider a scenario where each node has a rate limit L on the number of unique packets that it as a source can generate and send into the network within each time interval T. The time intervals start from time 0, T, 2T, etc. The packets generated within the rate limit are deemed genuine, but the packets generated beyond the limit are deemed flooded by this node. To defend against packet flood attacks, our goal is to detect if a node as a source has generated and sent more unique packets into the network than its rate limit L per time interval. The span of time interval should be set appropriately. If the interval is too long, rate limiting may not be very efficient against packet flood attacks. If the interval is too short, the number of associates that each node has during one interval may be too nondeterministic and thus it is difficult to set an appropriate rate limit. Generally speaking, the space should be short under the condition that most nodes can have a significant number of contacts with other nodes within one interval, but the appropriate length depends on the contact patterns between nodes in the specific deployment scenario. |
Defense against Replica Flood Attacks |
| As motivated in Section 2, the defense against replica flood considers single-copy and multi-copy routing protocols. These protocols need that, for each packet that a node buffers no matter if this packet has been generated by the node or forwarded to it, there is a limit l on the number of times that the node can forward this packet to other nodes. The values of l may be different for different buffered packets. Our goal is to detect if a node has violated the routing protocol and forwarded a packet more times than its limit l for the packet. A node’s limit l for a buffered packet is firm by the routing protocol. In multi copy routing, l ¼ L is a parameter of routing) if the node is the source of the packet, and l ¼ 1 if the node is an intermediate hop (i.e., it received the packet from another node). In single-copy routing, l ¼ 1 no matter if the node is the source or an intermediate hop. Note that the two limits L and l do not depend on each other. We discuss how to protect against replica flood attacks for quota-based routing. |
III. CLAIM-CARRY-AND-CHECK |
Packet Flood Detection |
| To detect the attackers that abuse their rate limit L, we must count the number of unique packets that each node as a basis has generated and sent to the network in the current interval. However, since the node may send its packets to any node it contacts at any time and place, no other node can monitor all of its sending behavior. To address this challenge, our idea is to let the node itself count the number of unique packets that it, as a source, has sent out, and claim the upto- date packet count (together with a little auxiliary information such as its ID and a timestamp) in each packet sent out. The node’s rate limit certificate is also attached to the packet, such that other nodes receiving the packet can learn its official rate limit L. |
| If an attacker is flooding more packets than its rate limit, it has to deceitfully claim a count smaller than the real value in the flooded packet, since the real value is larger than its rate limit and thus a clear indicator of attack. The claimed count must have been used before by the attacker in another claim, which is guaranteed by the pigeonhole principle, and these two claims are inconsistent. The nodes which have conventional packets from the attacker carry the claims included in those packets when they move around. When two of them contact, they check if there is any variation between their collected claims. The attacker is detected when an inconsistency is found. |
IV. THE INTELRATE CONTROLLER DESIGN |
| fuzzy logic traffic controller for controlling traffic in the network system defined Called the IntelRate, it is a TISO (Two-Input SingleOutput) controller. The TBO (Target Buffer Occupancy) q>0 is the queue size level we aim to achieve upon congestion. The queue deviation is one of the two inputs of the controller. In order to remove the steady state error, we choose the integration of e(t) as the other input of the controller, i.e. g |
Linguistic Description and Rule Base |
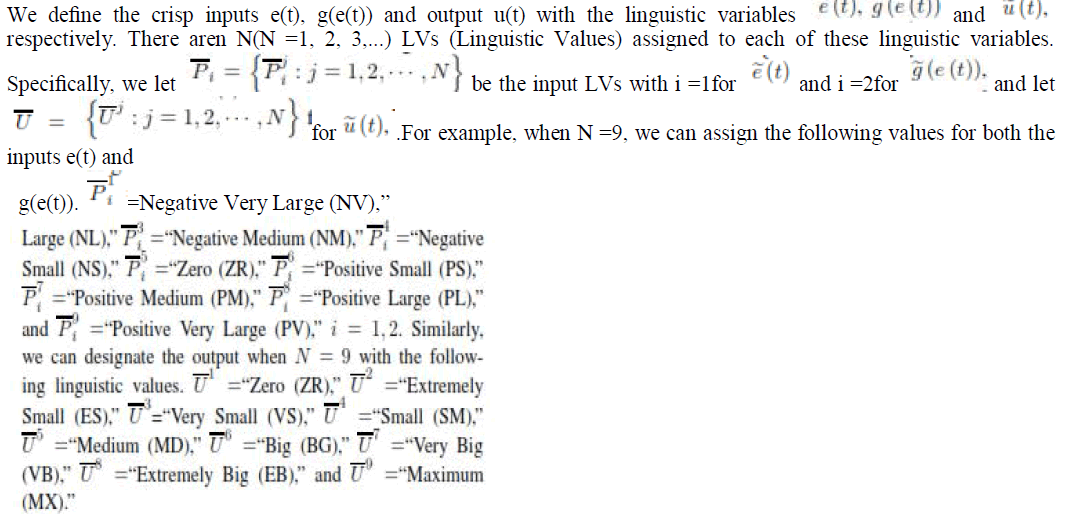 |
V. DELAY-BASED FLOW CONTROL |
Let  |
 |
| are important for solving problems of maximizing a concave function of a time average and are critical for network utility maximization with randomly arriving traffic [2], [28]. To ensure that the constraints (16) are satisfied, we use a virtual queue for each link , with update equation as follows: |
C. Delay-Based Lyapunov Function |
| We now impose the following structure on our control policy. Every slot, a packet transmission decision is made first.Ifa transmission over link l is successful (so that ), then the packet is removed from the queue, and no packet is dropped from link l (so that ). Else, if link either did not attempt transmission or if its transmission was unsuccessful, we can decide whether or not to drop the packet, but no other packet can be dropped from link l Thus, every slot ,we have |
 |
 |
VI. CONCLUSIONS |
| we employed rate limiting to ease flood attacks in DTNs, and a scheme which exploits claim-carry-and-check to probabilistically notice the violation of rate limit in DTN environments. Our scheme uses efficient constructions to keep the computation, communication and storage cost low. Also, we analyzed the lower bound and upper bound of detection probability We have established a delay-based policy for joint stability and utility optimization. The policy provides deterministic worst-case delay bounds, with total throughput value that is inversely proportional to the delay guarantee. The Lyapunov optimization approach for this delay-based problem is significantly different from that of backlog-based policies. We believe these results add significantly to our understanding of network delay and delayefficient control laws. |
References |
|