ISSN ONLINE(2320-9801) PRINT (2320-9798)
ISSN ONLINE(2320-9801) PRINT (2320-9798)
| Urvashi Manikpuri M.E Scholar, Department of ET&T, CSIT Durg, CSVTU University, Chhattisgarh, India |
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering
Image enhancement play an important role in Image processing and analysis. The enhancement techniques are Retinex algorithm, Unsharp masking and Histogram equalization. Here naturalness is essential for image enhancement to achieve pleasing perceptual quality. These algorithms can efficiently extract the details of images, they are prone to destroy the naturalness. In order to preserve naturalness while enhancing details, an enhancement algorithm for naturalness preservation is proposed to assess enhanced images. Firstly the measurement for naturalness preservation via Lightness Order Smoothing is done, secondly, decomposition of image via wavelet and thirdly, the process of transformation of image is carriedout so that the illumination will not flood the details which may happen due to spatial variation while lightness-order is preserved. Experimental result demonstrates that the proposed algorithm cannot only enhance the details but also preserve the naturalness of images.
Keywords |
| Image enhancement, lightness order smoothing, image decomposition, wavelet decomposition, logarithmic transformation. |
INTRODUCTION |
| This Image enhancement is basically improving the interpretability or perception of information in images for human viewers and providing `better' input for other automated image processing techniques. The principal objective of image enhancement is to modify attributes of an image to make it more suitable for a given task and a specific observer. The enhancement methods can broadly be divided in to the following two categories: |
| In spatial domain techniques, we directly deal with the image pixels. The pixel values are manipulated to achieve desired enhancement. In frequency domain methods, the image is first transferred into frequency domain. Its means that, these enhancement operations are performed in the Fourier Transform of the image is computed first. All the enhancement operations are performed on the Fourier transform of the image and then the Inverse Fourier Transform is performed to get the order to modify the image brightness, contrast or the distribution of the grey levels. As a consequence the pixel value (intensities) of the output image will be modified according to the transformation function applied on the input values. |
| There are some techniques used in image enhancement they are Retinex algorithm, Unsharp mask algorithm and Histogram Equalization. Retinex is an image enhancement algorithm that is used to improve the contrast, brightness and sharpness of an image primarily through dynamic range compression[4]. The algorithm also simultaneously provides color constant output and thus it removes the effects caused by different illuminants on a scene. It synthesizes contrast enhancement and color constancy by performing a non-linear spatial/spectral transform. The original algorithm is based on a model of human vision’s lightness and color constancy. Retinex belongs to the class of center surround functions, where each output value of the function is determined by the corresponding input value (center) and its neighborhood (surround). For Retinex the center is defined as each pixel value and the surround is a Gaussian function[4]. |
 |
| Histogram Equalization is a method in image processing of contrast adjustment using image histogram. An image histogram is a type of histogram that acts as a graphical representation of the tonal distribution in a digital image. It plots the number for each tonal value. The horizontal axis of the graph represents the tonal variations, while the vertical axis represents the number of pixels in that particular tone[5]. Unsharp Masking is an image sharpening technique, often available in digital image processing software. The “Unsharp” of the name derives from the fact that the technique uses an unsharp, positive image to create a mask of original image. The unsharped mask is then combined with the negative image, creating an image that is less blurry than the original[2]. |
| The main function of the proposed algorithm can not only enhance the details, but also maintains the naturalness for the non-uniform illumination images. The images enhanced by the proposed algorithm are visually pleasing, artifact free, and natural looking. By using lightness order smoothing the size of original image has reduced while scaling factor increases and entropy also decreases while intensity increases when scaling factor increases, dimension reduced and remain constant. Using wavelet decomposition for different levels size, dimension and entropy all are same but increasing the levels Intensity decrease and then increasing. By logarithmic transformation by increasing the scaling factors size and dimension increased and then remain constant. Normalized cross correlation is increased whereas entropy reduces. Intensity, Normalized absolute error, and Mean square error increased and then decreased then remain constant by increasing the scaling factor. |
II. RELATED WORK |
| In [1] authors make for preserving the naturalness by using retinex algorithm, unsharp masking and histogram equalization and enhancing details for non uniform illumination images. The ambience of the image should not be changed greatly after enhancement, no light source should be introduced to the scene, no halo effect should be added and no blocking effect should be amplified due to over-enhancement. Some natural enhancement algorithms based on Retinex theory are proposed to enhance details with the naturalness preserved. However, these algorithms are not suitable for non-uniform illumination images. Therefore, they propose a naturalness preserved enhancement algorithm for non-uniform illumination images in this paper, which not only enhances the details of the image but also preserves the naturalness. A LOE measure, which performs well in accordance with objective assessment on naturalness preservation, is proposed as well. Experimental results demonstrate that the images enhanced by the proposed algorithm are visually pleasing, artifact free, and natural looking. In [2] authors used unsharp masking is used for sharpness enhancement. Simultaneously enhanced contrast. Reducing the halo effect and finally solving the out-ofrange problem. In [3] author used an adaptive filter that controls the contribution of the sharpening path in such a way that contrast enhancement occurs in high detail areas and little or no image sharpening occurs in smooth areas. The adaptive filter does not perform a sharpening operation in smooth areas, and therefore the overall system is more robust to the presence of noise in the input images. The system is less sensitive to noise present in the input image. In [4] author used the Retinex algorithms are used to balance the illumination and to eliminate the shadow. It show very good reducing of the impact of uneven illumination and the presence of shadows and reducing the noise. In [5] author It can produce the output image with the mean intensity almost equal to the mean intensity of the input, thus fulfill the requirement of maintaining the mean brightness of the image. In BPDHE there is no parameter need to be tuned. BPDHE can enhance the images without introducing unwanted artifacts, while at the same time maintain the input brightness. |
III. PROPOSED ALGORITHM |
A. Description of the Proposed Algorithm: |
| Aim of the proposed algorithm is to enhance the details but also maintain the naturalness of an image and performance measurement . The proposed algorithm is consists of three main steps. |
Step 1: Calculating Lightness Order Smoothing: |
| The lightness order smoothing method aiming to enhance the details and preserving the naturalness simultaneously. It captured light which composed of reflex lightness (the lightness observed when illumination is uniform) and ambience illumination (the lightness observed when reflectance is uniform). The reflex lightness determines the details and the ambience illumination has an import impact on the naturalness. |
Step 2: Decomposition of Image: |
| Image decomposition means to decompose the image or to divide, to separate the components of an image. It can be done by wavelet decomposition. For understanding a wavelet decomposition firstly discuss wavelet, types and wavelet families. |
ïÃâ÷ Wavelet: |
| A wavelet is a wave-like oscillation with an amplitude that begins at zero, increases, and then decreases back to zero. It can typically be visualized as a "brief oscillation" like one might see recorded by a seismograph or heart monitor. Generally, wavelets are purposefully crafted to have specific properties that make them useful for signal processing. Wavelets can be combined, using a "reverse, shift, multiply and integrate" technique called convolution, with portions of a known signal to extract information from the unknown signal. As a mathematical tool, wavelets can be used to extract information from many different kinds of data, including – but certainly not limited to – audio signals and images. Sets of wavelets are generally needed to analyze data fully. A set of "complementary" wavelets will decompose data without gaps or overlap so that the decomposition process is mathematically reversible. Thus, sets of complementary wavelets are useful in wavelet based compression/decompression algorithms where it is desirable to recover the original information with minimal loss. There are two type of wavelet. They are discrete wavelet and continuous wavelet. |
ïÃâ÷ Wavelet Families: |
| There are different types of wavelet families whose qualities vary according to several criteria. The main criteria are: The support of Ãâñ and Ãâ°Ã¸, the speed of convergence to 0 of these functions(Ãâñ (t), or Ãâñ (ω)), when the time t or the frequency ω goes to infinity, which quantifies both time and frequency localizations. The symmetry, which is useful in avoiding dephasing in image processing. The number of vanishing moments for Ãâñ or for Ãâ°Ã¸ (if it exists), which is useful for compression purposes. |
| The regularity, which is useful for getting nice features, like smoothness of the reconstructed signal or image, and for the estimated function in nonlinear regression analysis. These are associated with two properties that allow fast algorithm and space-saving coding: |
| The existence of a scaling function Ãâ°Ã¸. The orthogonality or the biorthogonality of the resulting analysis .They may also be associated with these less important properties: |
| The existence of an explicit expression. The ease of tabulating. The familiarity with use. Typing waveinfo in commandline mode displays a survey of the main properties of all wavelet families available in the toolbox. Note that the Ãâñ and Ãâ°Ã¸ functions can be computed using wavefun; the filters are generated using wfilters. We provide definition equations for several wavelets. Some are given explicitly by their time definitions, others by their frequency definitions, and still others by their filters. |
| The following table outlines the wavelet families included in the toolbox. |
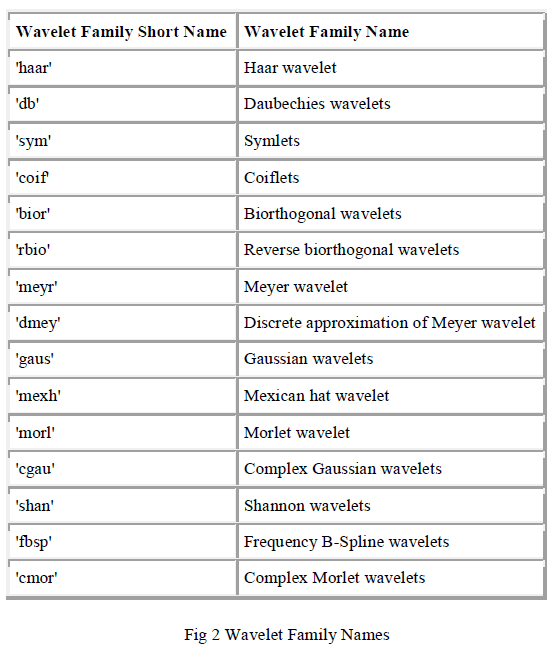 |
ïÃâ÷ Haar wavelets: |
| The Haar wavelet is a sequence of rescaled "square-shaped" functions which together form a wavelet family or basis. Wavelet analysis is similar to Fourier analysis in that it allows a target function over an interval to be represented in terms of an orthonormal function basis. |
| The Haar wavelet is also the simplest possible wavelet. The technical disadvantage of the Haar wavelet is that it is not continuous, and therefore not differentiable. This property can, however, be an advantage for the analysis of signals with sudden transitions, such as monitoring of tool failure in machines. |
| The Haar wavelet's mother wavelet function |
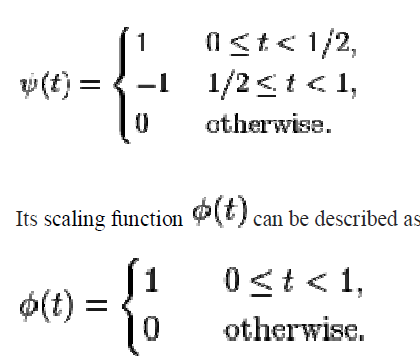 |
 |
| It is complete in L2(R): The Haar system on the line is an orthonormal basis in L2(R). |
| ïÃâ÷ Wavelet Decomposition: |
| It is multilevel 2-D wavelet decomposition. Wavelet decomposition produces a family of hierarchically organized decompositions. The selection of a suitable level for the hierarchy will depend on the signal and experience. Often the level is chosen based on a desired low-pass cutoff frequency. At each level j, we build the j-level approximation Aj, or approximation at level j, and a deviation signal called the j-level detail Dj, or detail at level j. We can consider the original signal as the approximation at level 0, denoted by A0. The words approximation and detail are justified by the fact that A1 is an approximation of A0 taking into account the low frequencies of A0, whereas the detail D1 corresponds to the high frequency correction. |
| Step 3: Image Transformation |
IV. SIMULATION RESULTS |
| The simulation studies involve the naturalness preservation via lightness order smoothing as shown in Fig.3 which enhance the details and preserved the naturalness. The Table 1 shows that the size of original image has reduced while scaling factor increases and entropy also decreases while intensity increases when scaling factor increases, dimension reduced and remain constant. The decomposition of images via wavelet decomposition as shown in fig.4 and Table 2 shows that for different levels size, dimension and entropy all are same but increasing the levels Intensity decrease and then increasing. |
 |
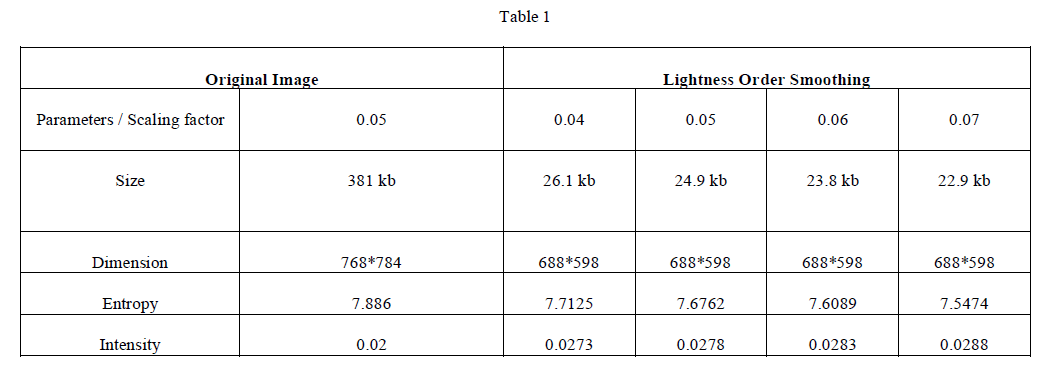 |
| Using lightness order smoothing the size of original image has reduced while scaling factor increases and entropy also decreases while intensity increases when scaling factor increases, dimension reduced and remain constant. It shown above Fig. 3 and Table 1. |
 |
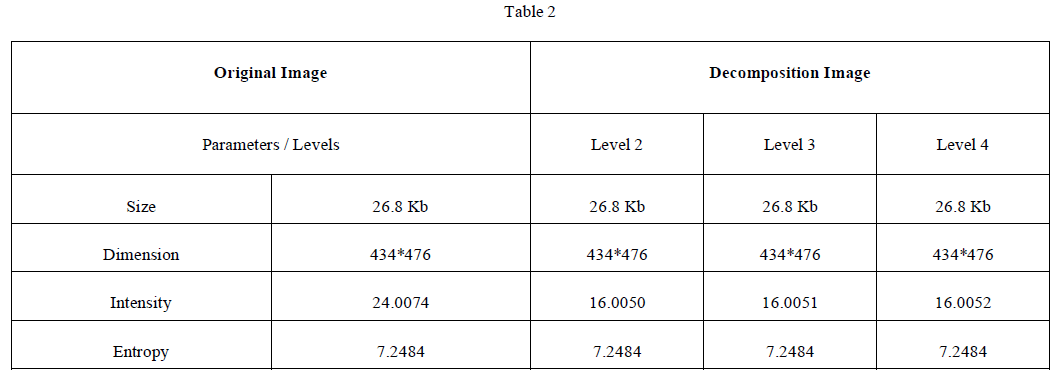 |
| By using wavelet decomposition for different levels size, dimension and entropy all are same but increasing the levels Intensity decrease and then increasing. It shown in Fig. 4 and Table 2. |
V. CONCLUSION AND FUTURE WORK |
| The simulation results showed that the proposed algorithm can not only enhance the details, but also maintains the naturalness for the non-uniform illumination images. The images enhanced by the proposed algorithm are visually pleasing, artifact free, and natural looking. Using lightness order smoothing the size of original image has reduced while scaling factor increases and entropy also decreases while intensity increases when scaling factor increases, dimension reduced and remain constant. By using wavelet decomposition for different levels size, dimension and entropy all are same but increasing the levels Intensity decrease and then increasing. |
References |
|