ISSN ONLINE(2320-9801) PRINT (2320-9798)
ISSN ONLINE(2320-9801) PRINT (2320-9798)
Malothu Nagu1, N.Vijay Shanker2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering
If the image is colored convert it in the gray scale image. Convert the image to double for better precision. Find the median by sorting all the values of the 3*3mask in increasing order. Replace the center pixel value with the median value. Estimate the Signal to Noise ratio. De convolution function is applied to filter the image. This Advanced filter is the combination of Median and Weiner filter. When we arrange these two filters in series we get the desired output. First we remove the impulse noise and then pass the result to the Weiner filter. The Weiner filter removes the blurredness and the additive white noise from the image. The result is not the same as the original image, but it is almost same.
Keywords |
| Median filter .Weiner filter ,denoising, Thresholding ,non-linear . |
INTRODUCTION |
| Image enhancement and restoration in a noisy environment are the basic problems in image processing. In order to improve the quality of images, there are various filtering techniques used in image processing. There are various filters which can remove the noise[1] from images and preserve image details. Some filters have been developed to remove either Gaussian or impulsive noise. These include the median filter and Weiner filters. Combination of these two filters has been used to remove mixed noise during image processing. Generally different filters are used for eliminating different noises like Mean filter is used to remove the impulse noise[1]. Median filtering is a nonlinear operation used in image processing to reduce "salt and pepper" noise. Weiner filter is to filter out noise that has corrupted a signal. It is based on a statistical approach. |
| Image noise is the random variation of brightness or color information in images produced by the sensor and circuitry of a scanner or digital camera. Image noise can also originate in film grain and in the unavoidable shot noise of an ideal photon detector. The Additive White Gaussian noise[6] is independent at each pixel and signal intensity. An image containing salt-and-pepper noise will have dark pixels in bright regions and bright pixels in dark regions he blurredness of the image is depend on the point spread function (psf) .The psf may circular or linear. The image is blurred due to the camera movement or the object displacement. |
II. LITERATURE SURVEY |
| Generally different filters are used for eliminating different noises[1] like mean filter & Weiner filter let us discuss them in detail given below .Median filtering is a nonlinear process useful in reducing impulsive, or salt-and-pepper noise. It is also useful in preserving edges in an image while reducing random noise. impulsive or salt-and pepper noise[2] can occur due to a random bit error in a communication channel. In a median filter, a window slides along the image, and the median intensity value of the pixels within the window becomes the output intensity of the pixel being processed. For example, suppose the pixel values within a window are 5,6, 55, 10 and 15, and the pixel being processed has a value of 55. the output of the median filter a current pixel location is 10, which is the median of the five values. |
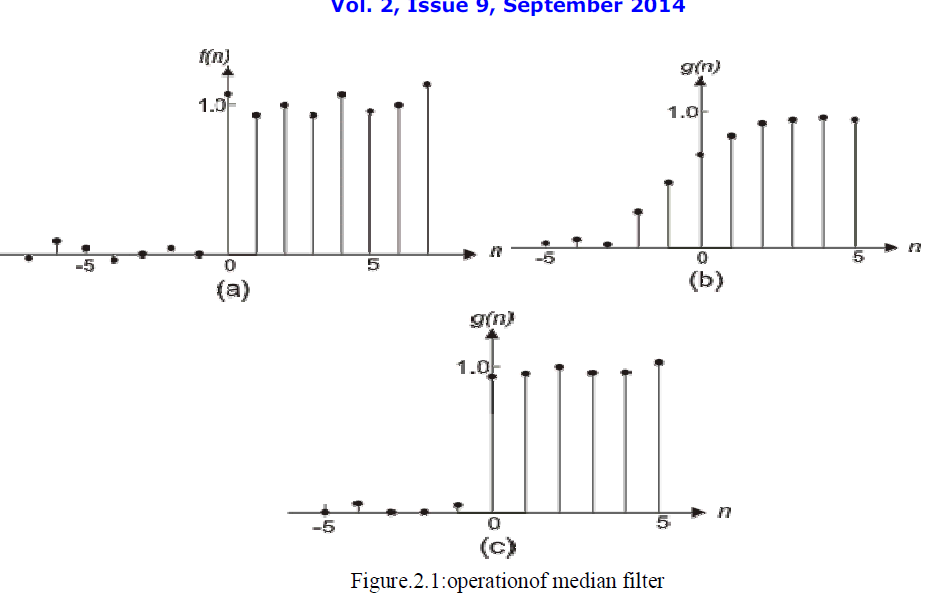 |
| Like low pass filtering, median filtering smoothes the image and is thus useful in reducing noise. Unlike low pass filtering, median filtering [4] can preserve discontinuities in a step function and can smooth a few pixels whose values differ significantly from their surroundings without affecting the other pixels. Figure (4.2) shows a 1-d step sequence degraded by a small amount of random noise. Figure (4.3) shows the result after filtering with a low pass filter whose impulse response is a 5-point rectangular window. Figure (4.4) shows the result after filtering with 5-point median filter. It is clear from the figure that the step discontinuity is better preserved by the median filter. Figure (a) shows a 1- d sequence with two values that are significantly different from the surrounding points. Figures (b) and (c) show the result of a low pass filter and a median filter, respectively. The filters used in figure (4.2) are the same as those used in figure (4.5). If the two impulsive values are due to noise, the result of using a median filter will be the reduce the noise. If the two values are part of the signal, however, using the median filter will distort the signal. |
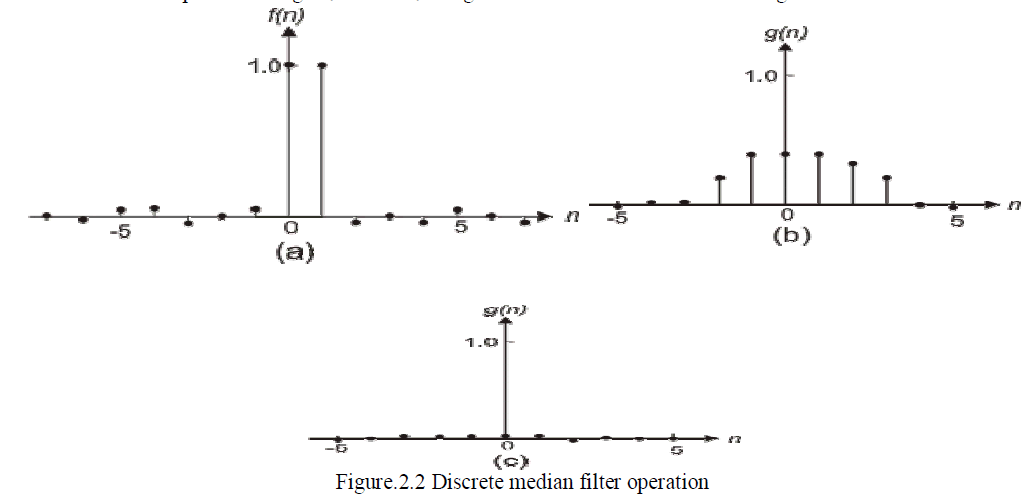 |
| The inverse filtering is a restoration technique for deconvolution [7], i.e., when the image is blurred by a known low pass filter, it is possible to recover the image by inverse filtering or generalized inverse filtering. However, inverse filtering is very sensitive to additive noise. The approach of reducing one degradation [5] at a time allows us to develop a restoration algorithm for each type of degradation and simply combine them. The Weiner filtering executes an optimal trade off between inverse filtering and noise smoothing. It removes the additive noise and inverts the blurring simultaneously. |
| The weiner filtering is optimal in terms of the mean square error. In other words, it minimizes the overall mean square error in the process of inverse filtering and noise smoothing. The weiner filtering is a linear estimation of the original image. The approach is based on a stochastic framework. The orthogonality principle implies that the weiner filter in Fourier domain can be expressed as follows: |
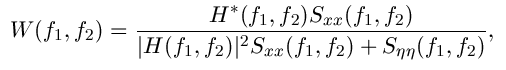 |
| Where |
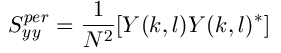 |
| Where y(k,l) is the dft of the observation. The advantage of the estimate is that it can be implemented very easily without worrying about the singularity of the inverse filtering[5]. Another estimate which leads to a cascade implementation of the inverse filtering and the noise smoothing is |
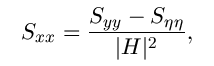 |
| Which is a straightforward result of the fact: |
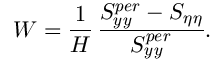 |
| The disadvantage of this implementation is that when the inverse filter is singular, we have to use the generalized inverse filtering. People also suggest the power spectrum of the original image can be estimated based on a model |
III. PROPOSED TECHINQUE |
| The proposed technique makes the use of cascading of two individual filters, median & weiner filters. Basically they are used to eliminate impulse noise and Gaussian noise[1] individually, But in this technique as both filters are used simultaneously, impulse noise[5] and Gaussian noise[6] are eliminated at a time. this technique is a bidirectional process. It is generally desirable for image brightness (or film density) to be uniform except where it changes to form an image. There are factors, however, that tend to produce variation in the brightness of a displayed image even when no image detail is present. This variation is usually random and has no particular pattern. In many cases, it reduces image quality and is especially significant when the objects being imaged are small and have relatively low contrast. This random variation in image brightness is designated noise. |
| This Advanced filter is the combination of Median and weiner filter. When we arrange these two filters in series we get the desired output. First we remove the impulse noise[6] and then pass the result to the weiner filter. The weiner filter moves the blurredness and the additive white noise from the image. The result is not the same as the original image, but it is almost same. The block diagram for advanced filter is given below: |
 |
| Image noise is the random variation of brightness or color information in images produced by the sensor and circuitry of a scanner or digital camera. Image noise can also originate in film grain and in the unavoidable shot noise[6] of an ideal photon detector. Image noise is generally regarded as an undesirable by-product of image capture. The types of Noise are following:- |
| 1. Additive White Gaussian noise |
| 2. Salt-and-pepper noise |
| 3. Blurredness |
Additive White Gaussian noise |
| The Additive White Gaussian noise is independent at each pixel and signal intensity. In color cameras where more amplification is used in the blue color channel than in the green or red channel, there can be more noise in the blue channel. |
Salt-and-pepper noise |
| An image containing salt-and-pepper noise will have dark pixels in bright regions and bright pixels in dark regions [2].This type of noise can be caused by dead pixels, analog-to digital converter errors, bit errors in transmission, etc. This can be dark/bright pixels. |
Blurredness |
| The blurredness of the image is depend on the point spread function (psf) .The psf may circular or linear. The image is blurred due to the camera movement or the object displacement. |
Median Filter |
| To understand what adaptive median filtering [2] is all about, one first needs to understand what a median filter is and what it does. In many different kinds of digital image processing, the basic operation is as follows: at each pixel in a digital image we place a neighbourhood around that point, analyse the values of all the pixels in the neighbourhood according to some algorithm, and then replace the original pixel's value with one based on the analysis performed on the pixels in the neighbourhood. The neighbourhood then moves successively over every pixel in the image, repeating the process. |
| Median filtering follows this basic prescription. The median filter[2] is normally used to reduce noise in an image, somewhat like the mean filter. However, it often does a better job than the mean filter of preserving useful detail in the image. This class of filter belongs to the class of edge preserving smoothing filters which are non-linear filters. This means that for two images A(x) and B(x): |
 |
| These filters[2] smooth’s the data while keeping the small and sharp details. The median is just the middle value of all the values of the pixels in the neighbourhood. Note that this is not the same as the average (or mean); instead, the median has half the values in the neighbourhood larger and half smaller. The median is a stronger "central indicator" than the average. In particular, the median is hardly affected by a small number of discrepant values among the pixels in the neighbourhood. Consequently, median filtering is very effective at removing various kinds of noise. Figure 3.2 illustrates an example of median filtering. |
 |
| Like the mean filter[2], the median filter[6] considers each pixel in the image in turn and looks at its nearby neighbours to decide whether or not it is representative of its surroundings. Instead of simply replacing the pixel value with the mean of neighbouring pixel values, it replaces it with the median of those values. The median is calculated by first sorting all the pixel values from the surrounding neighbourhood into numerical order and then replacing the pixel being considered with the middle pixel value. (If the neighbourhood under consideration contains an even number of pixels, the average of the two middle pixel values is used.) Figure 4.3 illustrates an example calculation. |
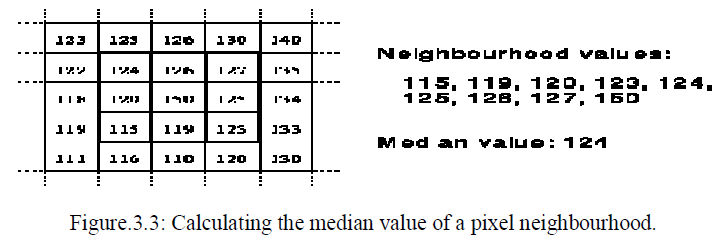 |
| As can be seen, the central pixel value of 150 is rather unrepresentative of the surrounding pixels and is replaced with the median value: 124. A 3×3 square neighbourhood is used here --- larger neighbourhoods will produce more severe smoothing. |
D.Noise |
| Noise is any undesirable signal. Noise is everywhere and thus we have to learn to live with it. Noise gets introduced into the data via any electrical system used for storage, transmission, and/or processing. In addition, nature will always plays a "noisy" trick or two with the data under observation. When encountering an image corrupted with noise you will want to improve its appearance for a specific application. The techniques applied are application-oriented. Also, the different procedures are related to the types of noise[7] introduced to the image. Some examples of noise are: Gaussian or White, Rayleigh, Shot or Impulse, periodic, sinusoidal or coherent, uncorrelated, and granular[7]. |
Purpose |
| 1). Remove impulse noise |
| 2). Smoothing of other noise |
| 3). Reduce distortion, like excessive thinning or thickening of object boundaries Adaptive median filter changes size of Sxy (the size of the neighbourhood) during operation. |
Notation |
| Zmin = minimum gray level value in Sxy |
| Zmax = maximum gray level value in Sxy |
| Zmed = median of gray levels in Sxy |
| Zxy = gray level at coordinates (x, y) |
| Smax = maximum allowed size of Sxy |
 |
Advantages |
| The standard median filter does not perform well when impulse noise is |
| a. Greater than 0.2, while the adaptive median filter can better handle these noises. |
| b. The adaptive median filter preserves detail and smooth non-impulsive noise, while the standard median filter does not. |
| See examples in figure given in a & b (with a probability of 0.1). |
 |
E. Weiner Filter |
| The goal of the Weiner filter [3]is to filter out noise that has corrupted a signal. It is based on a statistical approach. Typical filters are designed for a desired frequency response. The Weiner filter approaches filtering[5] from a different angle. One is assumed to have knowledge of the spectral properties of the original signal and the noise, and one seeks the LTI filter whose output would come as close to the original signal as possible [1]. Weiner filters are characterized by the following: |
| a. Assumption: signal and (additive) noise are stationary linear random processes with known spectral characteristics. |
| b. Requirement: the filter must be physically realizable ,i.e. causal (this requirement can be dropped, result ingin a noncausal solution). |
| c. Performance criteria: minimum mean-square error. |
Weiner Filter in the Fourier Domain |
| The weiner filter is given by following transfer function: |
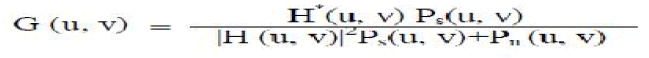 |
| Dividing through by Ps makes its behaviour easier to explain: |
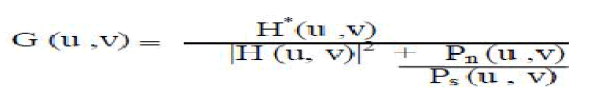 |
| Where |
| H (u, v) = Degradation function |
| H*(u, v) = Complex conjugate of degradation function |
| Pn (u, v) = Power Spectral Density of Noise |
| Ps (u, v) = Power Spectral Density of un-degraded image. |
| The term Pn /Ps can be interpreted as the reciprocal of the signal-to-noise ratio. |
| Weiner filtering is a general way of finding the best reconstruction of a noisy signal (in L2 norm)– applies in any orthogonal function basis– different bases give different results |
| • best when the basis most cleanly separates signal from noise |
| • The “universal” Weiner filter is to multiply components by S2/(S2+N2) |
| – smooth tapering of noisy components towards zero |
| • In Fourier basis, the Weiner filter is an optimal low-pass filter |
| – learn how the frequencies of an FFT are arranged! |
| – this is useful in many signal processing applications |
| – but for images, it loses spatial resolution |
| • In spatial (pixel) basis, the Weiner filter is usually applied to the difference between an image and a smoothed image |
| • In a wavelet basis, components encode both spatial and frequency information |
| – largest magnitude components often have the least noise |
| – so Weiner filtering can preserve resolution |
| • There are two key ideas behind wavelets (such as the DAUB family) |
| – quadrature mirror filters |
| – pyramidal algorithm |
| This general idea can be applied whenever you have a basis in function space that concentrates “mostly signal” in some components relative to “mostly noise” in others. |
| You cloud just set components with too much noise to zero. Weiner filtering is better: it gives the optimal way of tapering off the noisy components, so as to give the best (L2 norm) reconstruction of the original signal. Can be applied in spatial basis (delta functions, or pixels), Fourier basis (frequency components), wavelet basis, etc. Different bases are not equivalent, because, in particular problems, signal and noise distribute differently in them. A lot of signal processing is finding the right basis for particular problems – in which signal is most concentrated. |
IV. SIMULATION RESULT |
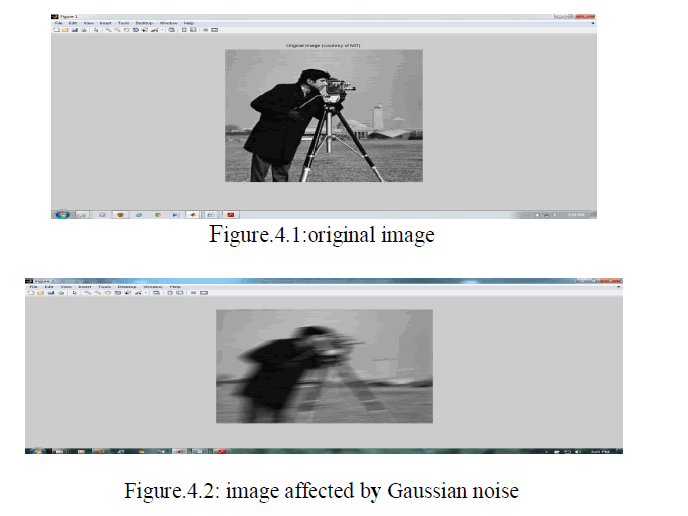
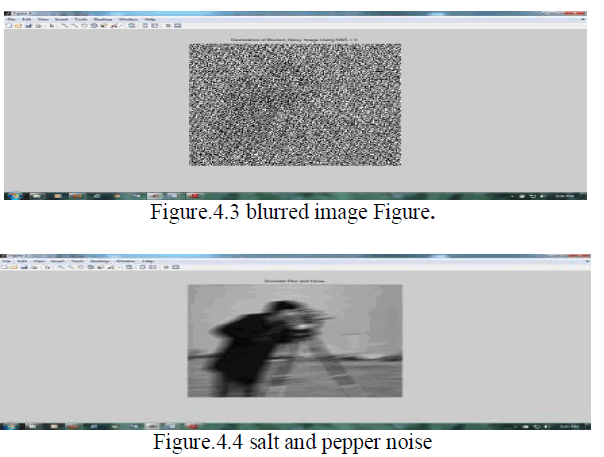
| The Original Image is cameraman image.Adding three types of Noise (Additive white Gaussian noise, Salt & Pepper noise blurredness) and pass this image to our hybrid filter we get the desired result. The results depend upon the blurring angle (theta) and the blurring length (Len) and the intensity of the impulse noise. The performance is compared with the MSE & PSNR of the original image and the filter output image. The proposed efficient algorithm is implemented with MATLAB. |
A.SIMULATION TO WEINER FILTER |
| The goal of the Weiner filter [3 is to filter out noise that has corrupted a signal. It is based on a statistical approach. Typical filters are designed for a desired frequency response. The Weiner filter approaches filtering [5] from a different angle. One is assumed to have knowledge of the spectral properties of the original signal and the noise, and one seeks the LTI filter whose output would come as close to the original signal as possible [1]. |
 |
B.SIMULATION TO MEDIAN FILTER |
| Median filtering follows this basic prescription. The median filter[2] is normally used to reduce noise in an image, somewhat like the mean filter. However, it often does a better job than the mean filter of preserving useful detail in the image. This class of filter belongs to the class of edge preserving smoothing filters which are non-linear filters. |
 |
 |
· VI. CONCLUSION AND FUTURE SCOPE |
| We used the cameraman image in .tif format and adding three noises (impulse noise, Gaussian noise, blurredness) and apply the noisy image to the advanced filter. The final images nearly same as the original image. The filtered image is depending upon the blurring angle and the blurring length and the percentage of the impulse noise. When these variables are lesser in amount the filtered image is nearly equal to the original image. There are a couple of areas which we would like to improve on. One area is in improving the de-noising along the edges as the method we used did not perform so well along the edges .Instead of using the median filter we can use the adaptive median filter. |
References |
|