ISSN ONLINE(2320-9801) PRINT (2320-9798)
ISSN ONLINE(2320-9801) PRINT (2320-9798)
Sandeep Kaur1, Navdeep Singh 2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering
The main challenge in digital image processing is to remove noise from the original image. This paper reviews the existing denoising algorithms and performs their comparative study. Different noise models including additive and multiplicative types are discussed in the paper.Selection of the denoising algorithm is application dependent. Hence, it is necessary to have knowledge about the noise present in the image so as to select the appropriate denoising algorithm. Here we put results of different approaches of wavelet based image denoising methods using several thresholding techniques such as BayesShrink,SureShrink, and VisuShrink.A quantitative measure of comparison is provided by SNR (signal to noise ratio) and mean square error (MSE).
Keywords |
| Wavelet transforms, Spatial Filtering, BayesShrink, SureShrink, and VisuShrink |
INTRODUCTION |
| Digital images plays very significant role in our daily routine like they are used in satellite television, Intelligent traffic monitoring, handwriting recognition on checks, signature validation, computer resonance imaging and in area of research and technology such as geographical information systems and astronomy. In digital imaging, the acquisition techniques and systems introduce various types of noises and artifacts. Denoising is more significant than any other tasks in image processing, analysis and applications. Reserving the details of an image and removing the random noise as far as possible is the goal of image denoising approaches. Besides the noisy image produces undesirable visual quality, it also lowers the visibility of low contrast objects. Hence noise removal is essential in digital imaging applications in order to enhance and recover fine details that are hidden in the data. In many occasions, noise in digital images is found to be additive in nature with uniform power in the whole bandwidth and with Gaussian probability distribution. Such a noise is referred to as Additive White Gaussian Noise (AWGN). It is difficult to Suppress AWGN since it corrupts almost all pixels in an image [1]-[2]. In denoising there is always a tradeoff between noise suppression and preserving actual image discontinuities. To remove noise without excessive smoothing of important details, a denoising technique needs to be spatially adaptive. Different techniques are used depending on the noise model. Due to properties like sparsity, an edge detection and multiresolution , the wavelets naturally facilitates such spatially adaptive noise filtering [3]. |
| The paper is organized as follows: Section II contains Evolution of Image Denoising Techniques. Section III contains survey of the related work in which various image denoising techniques are explained and then comparison of these methods is given in table2. |
II. EVOLUTION OF IMAGE DENOISING TECHNIQUES |
| Image denoising is the fundamental problem in Image processing. Wavelet gives the excellent performance in field of image denoising because of sparsity and multiresolution structure. With the popularity of Wavelet Transform for the last two decades, several algorithms have been developed in wavelet domain. The focus was shifted to Wavelet domain from spatial and Fourier domain. Ever since the Donoho’s wavelet based thresholding approach was published in 2003, there was surge in the image denoising papers being published. Although his approach was not revolutionary, it did not require tracking and correlation of the wavelet maxima and minima across the different scales as proposed by Mallat [4].Thus there was renewed interest in wavelet approach since Donoho’s [5] demonstrated a simple solution to difficult problem domain. Researchers published different approaches to compute the simulation parameters for wavelet coefficients. To achieve optimum threshold value , data adaptive threshold [6] were introduced. Substantial improvements in perceptual quality could be obtained by translation invariant method based on thresholding of an Undecimated Wavelet transform [7]. Much effort has been devoted to Bayesian denoising in wavelet domain. Gaussian scale mixtures and hidden markov models have also become popular and more research is continued to be published and Independent component analyses (ICA) have been explored in data adaptive components. Different statistical models are focused to model the statistical properties of wavelet coefficients and its neighbours. Future trend will be to find more probabilistic model for non-orthogonal wavelet coefficients distribution. |
III. RELATED WORK |
| There has been a significant amount of work done on image denoising techniques. Existing methods are able to produce good results in many practical scenarios. The various denoising techniques are as follows: |
| Spatial Filtering: A traditional way to remove noise from image data is to employ spatial filters. Spatial filtering is commonly used to clean up the output of lasers, removing aberrations in the beam due to imperfect , dirty or damaged optics. Spatial filters can be further classified into non-linear and linear filters. |
| Linear Filters: Linear filters process time-varying input signals to produce output signals, subject to constraint of linearity. A mean filter is the optimal linear filter for Gaussian noise in the sense of mean square error. Linear filters too tend to blur sharp edges, destroy lines and other fine image details, and perform poorly in the presence of signal-dependent noise. The wiener filtering [11] method requires the information about the spectra of the noise and the original signal and it works well only if the underlying signal is smooth. Wiener method implements spatial smoothing and its model complexity control correspond to choosing the window size. To overcome the weakness of the Wiener filtering, Donoho and Johnstone proposed the wavelet based denoising scheme in [12, 13]. |
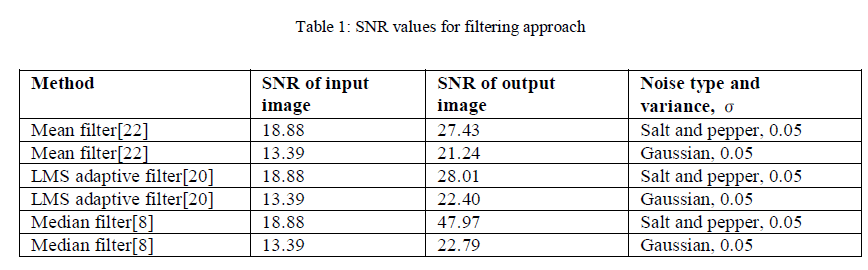
| Mean Filter: A mean filter [22] acts on an image by smoothing it; that is, it reduces the intensity variation between adjacent pixels. The mean filter is nothing but a simple sliding window spatial filter that replaces the center value in the window with the average of all the neighboring pixel values including itself. Image corrupted with salt and pepper noise is subjected to mean filtering and it can be observed that the noise dominating is reduced . The white and dark pixel values of the noise are changed to be closer to the pixel values of the surrounding ones. Also, the brightness of the input image remains unchanged because of the use of the mask, whose coefficients sum up to the value one.The mean filter is used in applications where the noise in certain regions of the image needs to be removed. In other words, the mean filter is useful when only a part of the image needs to be processed. |
| LMS Adaptive Filter: Adaptive filters are capable of denoising non-stationary images, that is, images that have abrupt changes in intensity. Such filters are known for their ability in automatically tracking an unknown circumstance or when a signal is variable with little a priori knowledge about the signal to be processed [20].An adaptive filter does a better job of denoising images compared to the averaging filter as the Least Mean Square (LMS) adaptive filter is known for its simplicity in computation and implementation. The LMS adaptive filter works well for images corrupted with salt and pepper type noise. But this filter does a better denoising job compared to the mean filter. |
| Non-linear filters: Non-linear filters have many applications, especially in removal of certain types of noise that are not additive. Generally spatial filters remove noise to a reasonable extent but at the cost of blurring images which in turn makes the edges in pictures invisible. In recent years, a variety of nonlinear median type filters such as weighted median [8], rank conditioned rank selection [9], and relaxed median [10] have been developed to overcome this drawback. |
| Median Filter: The median filter also follows the moving window principle similar to the mean filter. A 3×3,5×5, or 7×7 kernel of pixels is scanned over pixel matrix of the entire image. The median of the pixel values in the window is computed, and the center pixel of the window is replaced with the computed median. The median is more robust compared to the mean. Thus, a single very unrepresentative pixel in a neighborhood will not affect the median value significantly.Since the median value must actually be the value of one of the pixels in the neighborhood, the median filter does not create new unrealistic pixel values when the filter straddles an edge. For this reason the median filter is much better at preserving sharp edges than the mean filter. These advantages aid median filters in denoising uniform noise as well from an image. |
| Spatial Median Filter : The spatial median filter is also noise removal filter where the spatial median is calculated by calculating the spatial depth between a point and a set of point. In this filter after finding out the spatial depth of each point lying within the filtering mask, this information is used to decide whether the central pixel of window is corrupted or not, If central pixel is uncorrupted then it will not be changed. We then find out the spatial depth of each pixel within the mask and then sort these spatial depths in descending order .The point with largest spatial depth represent the spatial median of the set. |
| Weighted Median Filter (WMF) :The centre weighted median filter is an extension of the weighted median filter. The weighted median filter previously designed gives more weight to some values within the window whereas centre weighted median filter gives more weight to the central value of a window thus easier to design and implement than other weighted median filter. |
| Wavelet Transforms:Wavelets are mathematical functions that analyze data according to scale or resolution [18]. They aid in studying a signal in different windows or at different resolutions. For instance, if the signal is viewed in a large window, gross features can be noticed, but if viewed in a small window, only small features can be noticed. Wavelets provide some advantages over Fourier transforms. For example, they do a good job in approximating signals with sharp spikes or signals having discontinuities. The wavelet equation produces different wavelet families like Daubechies, Haar, Coiflets, etc. [19]. |
| Mallat’s Algorithm:Mallat’s algorithm [21] is a computationally efficient method of implementing the wavelet transform. It calculates DWT wavelet coefficients for a finite set of input data, which is a power of 2. This input data is passed through two convolution functions, each of which creates an output stream that is half the length of the original input. This procedure is referred to as down sampling . Once the processing is done, the data vector is built back from the coefficients. This processes of reconstruction is referred to as the inverse Mallat’s algorithm. |
| Tables 1 shows the SNR (signal to noise ratio) of the input and output images for the filtering approach . It shows how SNR varies with different type of noise and filters used. |
 |
| Wavelet Thresholding:Donoho and Johnstone [17] pioneered the work on filtering of additive Gaussian noise using wavelet thresholding. Wavelet coefficients calculated by a wavelet transform represent change in the time series at a particular resolution. By considering the time series at various resolutions, it is then possible to filter out noise.The term wavelet thresholding is explained as decomposition of the data or the image into wavelet coefficients, comparing the detail coefficients with a given threshold value, and shrinking these coefficients close to zero to take away the effect of noise in the data. The image is reconstructed from the modified coefficients. There are various thresholding techniques. Some of these are discussed below: |
| VisuShrink:VisuShrink was introduced by Donoho [16]. It uses a threshold value t that is proportional to the standard deviation of the noise. It follows the hard thresholding rule. It is also referred to as universal threshold and is defined as t =σ 2log n |
| VisuShrink does not deal with minimizing the mean squared error [15]. It can be viewed as general-purpose threshold selectors that exhibit near optimal minimax error properties and ensures with high probability that the estimates are as smooth as the true underlying functions [16]. However, VisuShrink is known to yield recovered images that are overly smoothed. This is because VisuShrink removes too many coefficients. Another disadvantage is that it cannot remove speckle noise. It can only deal with an additive noise. VisuShrink follows the global thresholding [14] scheme where there is a single value of threshold applied globally to all the wavelet coefficients. |
| SureShrink:A threshold chooser based on Stein’s Unbiased Risk Estimator (SURE) was proposed by Donoho and Johnstone [17] and is called as SureShrink. It is a combination of the universal threshold and the SURE threshold. The SureShrink threshold t* is defined as t* = min (t,σ 2log n ) |
| where t denotes the value that minimizes Stein’s Unbiased Risk Estimator, σ is the noise variance and n is the size of the image. |
| SureShrink follows the soft thresholding rule. SureShrink suppresses noise by thresholding the empirical wavelet coefficients. SureShrink produces the best SNR as compared to VisuShrink and BayesShrink. |
| BayesShrink:BayesShrink was proposed by Chang, Yu and Vetterli [15]. The goal of this method is to minimize the Bayesian risk, and hence its name, BayesShrink. It uses soft thresholding and is subband-dependent, which means that thresholding is done at each band of resolution in the wavelet decomposition. Like the SureShrink procedure, it is smoothness adaptive. The Bayes threshold, tB, is defined as tB =σ2 /σ s . |
| where σ2 is the noise variance and σ2 is the signal variance without noise. |
| The output from BayesShrink method is much closer to the high quality image and there is no blurring in the output image unlike the other two methods. |
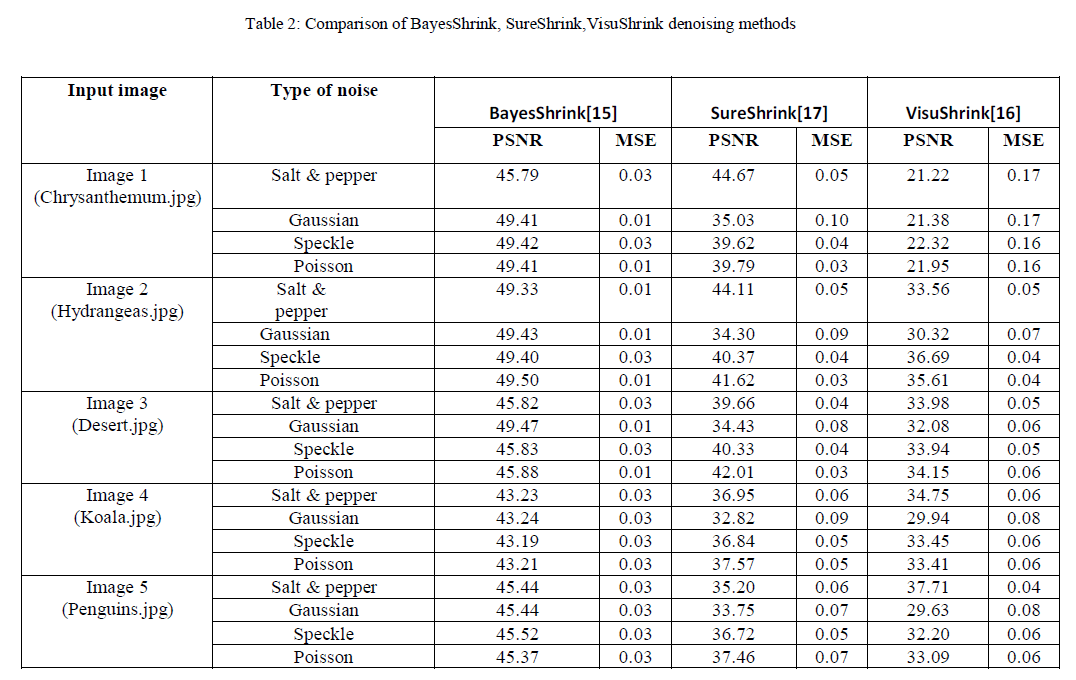
| Table 2 shows the comparison of three thresholding methods used for image denoising for five different images. The output is dependent on respective method used and the simulated results in terms of PSNR ( peak signal to noise ratio) and MMSE (minimum mean square error). |
 |
IV. CONCLUSION |
| In this paper different denoising techniques are discussed. It can be concluded that for salt and pepper noise, the median filter is optimal compared to mean filter and LMS adaptive filter. It produces the maximum SNR for the output image compared to the linear filters considered. The LMS adaptive filter proves to be better than the mean filter but has more time complexity. The image obtained from the median filter has very less noise present in it and is close to the high quality image. The sharpness of the image is retained unlike in the case of linear filtering. In the case where an image is corrupted with Gaussian noise, the wavelet shrinkage denoising has proved to be nearly optimal. SureShrink produces the best SNR compared to VisuShrink and BayesShrink. However, the output from BayesShrink method is much closer to the high quality image and there is no blurring in the image unlike the other two methods. VisuShrink cannot denoise multiplicative noise unlike BayesShrink. From the obtained results it is visible that BayesInvariant thresholding technique in comparison has the highest PSNR values and minimum MMSE. SureShrink technique has high PSNR and comparatively high MMSE as compared to BayesInvariant thresholding technique. On the other hand VisuShrink method takes highest computation time and has lowest PSNR and much Higher MMSE vales. An important point to note is that although SureShrink performed a little poor than BayesInvariant based on PSNR and MMSE denoising, it adapts well to sharp discontinuities in the image. Thus to summarize BayesInvariant thresholding technique has best performance, SureShrink is better whereas VisuShrink is comparatively poor in performance. |
References |
|