Impact of Route Stability under
Random Based Mobility Model in
MANET

DR.K.P.KALIYAMURTHIE; D.PARAMESWARI

Impact of Route Stability under Random Based Mobility Model in MANET

DR.K.P.KALIYAMURTHIE¹, D.PARAMESWARI²

Professor and Head, Dept. of IT, Bharath University, Chennai-600 073
Asst. Prof. (SG), Dept. of Computer Applications, Jerusalem College of Engg., Chennai-600 100

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering

Abstract

A basic issue arising in mobile ad hoc networks (MANETs) is the selection of the optimal path between any two nodes. A method that has been advocated to improve routing efficiency is to select the most stable path so as to avoid packet losses and limit the latency and overhead due to path reconstruction. In the existing system, the work in considers nodes moving along non random patterns where nodes start moving from the same location. It causes short route disruption. This fact makes the analysis more complex but at the same time permits to relate probability of link duration and/or availability at time t to the initial distance between nodes. To avoid this problem, In proposed system nodes moving along random direction model. The links along a path may fail and an alternate path must be found. Through our results, we study the problem of selecting an optimal route in terms of path availability. Finally, we propose an approach to improve the efficiency of reactive Routing protocols.

Keywords

Mobile ad hoc networks, Routing, Modeling and analysis

INTRODUCTION

Mobile wireless networks are receiving an increasing interest due to the possibility of ubiquitous communications. In particular, mobile ad hoc networks enable users to maintain connectivity to be fixed network or exchange information when no infrastructure, such as base station or an access point is available.This is achieved through multihop communication, which allow a node to reach far away destinations by using intermediate nodes as relays. This project proposes node mobility, signal interference, and power outages make the network topology frequently change; as a consequence the links along a path may fail and alternate path must be found. A method that has been advocated to improve the routing efficiency is to select the most stable path as to avoid packet losses and the limit the latency and overhead due to path reconstruction

A mobile ad hoc network (MANET) is a collection of mobile wireless devices or nodes that communicate with each other. The transmission range of a wireless node is the maximum distance within which the signals received from the node can be used to extract meaningful information. Two nodes within each other’s transmission range can communicate directly. If two nodes are not within each other’s transmission range, they have to communicate using a multi-hop route involving one or more intermediate nodes. Since wireless devices operate with limited battery power, they are often configured to work on a smaller transmission range. So, multi-hop routing is more common in MANETs.

A mobility model is used to capture the movement of a real-world object in simulation studies. In MANETs, a mobility model is used to define the movement of a mobile wireless node (shortly referred hereafter as MN). There are two types of MANET mobility models: single-entity and group

II. PROPOSED SYSTEM

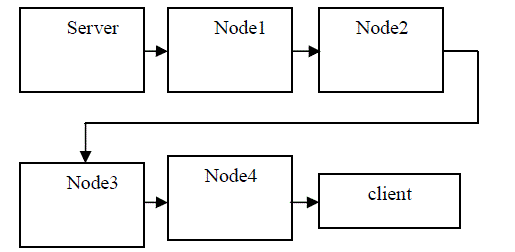
The proposed system is divided into four modules as shown in the following figure. The modules are implemented in .Net

III. MODULES

This section contains the following modules namely,

A. Expression for transform of distribution

B. Probability of path duration and availability.

C. Link correlation.

D. Performance evaluation.

A. Expression for transform of distribution

We derive for the first time an expression for the transform of the distribution of a node moving according to the RD model. This expression can be numerically inverted to obtain the temporal evolution of the probability density function of the no deposition, given an assigned initial condition. Closed form expressions for the temporal evolution of the distribution moments can also be derived directly from the transform

We consider the Random Direction model, i.e., each node alternates periods of movement (move phase) to periods during which it pauses (pause phase); at the beginning of each move phase, a node independently selects its new direction and speed of movement. Speed and direction are kept constant for whole duration of the node move phase; the duration of move and pause phases are, in general, distributed according to independent random variables.

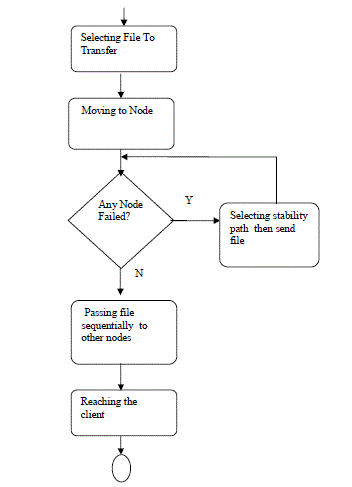
Expression for transform of distribution consist of following steps.

Select Receiving Path

In this step first select the receiving path button. It is used to create a file or folder where we want after the transformation from the server.

Create New Folder

Once Selected the path, we have to create the new folder. If the file is not created or cancelled then we can’t receive the file and also message box shows “please select a file receiving path else you cannot receive the file”.

Running and Waiting to Receive

If the file has been created then process is running and waiting to receive the path of the file. Once file is received, then it is automatically set the path of the file.

It is known as receiving path file.

For Example:

C:\documents and settings\Desktop\File name

B. Probability of path duration and availability

We propose a simple, approximate expression for the probability of link availability under the RD model, which leverages the derivation of the second moment of the node spatial distribution. Our findings suggest that as time proceeds, the probability of link availability under a generic mobility be obtained through a similar approximation. The same approach can be applied o the computation of the probability of path duration.

An exact expression for the link duration probability under the RD model appears prohibitive for the following reasons:

The relative motion between two nodes moving according to independent RD motions is no longer an RD motion. In principle, the relative motion between nodes A and B can be described in terms of a Markov Process over a general state space and obtained by solving the corresponding Chapman- Kolmogorov equations. However, the dimensionality of the state space increases since the instantaneous system state is characterized by 1) the phases of the nodes; 2) the instantaneous relative position and 3) the current speed of the two nodes VA(t) and VB(t).

The obtained Chapman-Kolmogorov equations should be solved over a circular spatial domain of radius R, with absorbing boundary conditions. However, the structure of the equations describing the relative motion becomes much more complex

when they are expressed in polar coordinates, and any attempt to apply the methodology of separation of variables fails

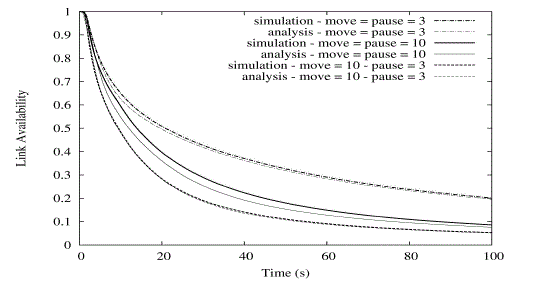
Fig. 3. Probability of link availability versus time in case of the RD model. Different curves correspond to different values of the average duration of the move and pause phases.

C. Link correlation

Based on our results on the probabilities of link availability and link duration, we study the same matrices for multihop paths, again in the case of RD mobility. We discuss the validity of the link independence assumption, which is widely used, and compared it against a refined assumption that accounts for link correlation. We observe that the link independence assumption provides sufficiently accurate results.

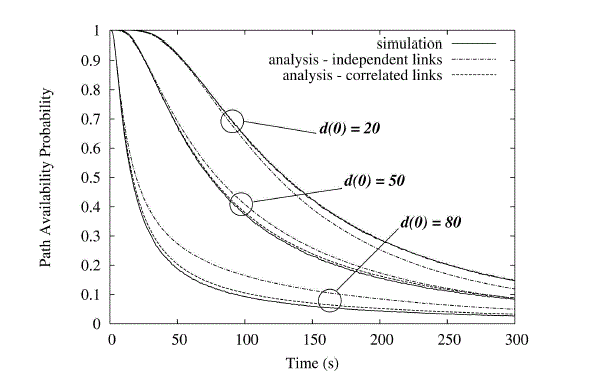
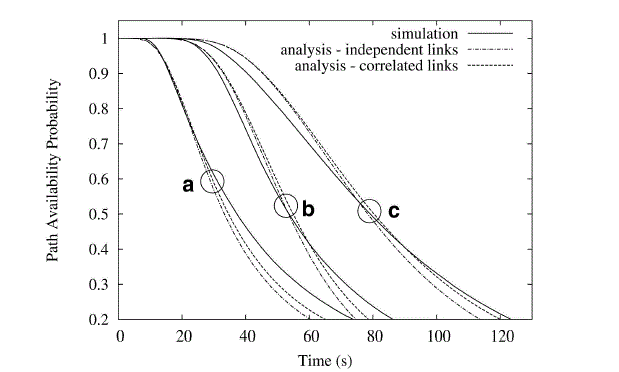
We now evaluate the accuracy of our approximations for the path availability, comparing analytical and simulation results. Fig. 4 presents the probability that a path consisting of three hops is available, with all of the hops having the same initial length, namely, 20, 50, and 80 m. We first consider a Brownian motion with _2 ¼ 12 m2=s (a typical value for a scenario of human mobility) and R ¼ 100 m so as to assess the impact of the approximations introduced for multihop paths without any additional source of error. Simulation results are compared with the approximation based on the link independence assumption, and with our improved approximation that partially accounts for the correlation among links. We observe that the improved approximation gets very close to the simulation results in all considered cases. The independence assumption slightly underestimates the probability of path availability for an initial hop length of 20 m, whereas overestimates it in the other two cases. From extensive experiments, we have arrived at the conclusion that, in general, the results obtained under the independence assumption are less accurate when the initial length of the hops is close to the radio range (see the case d(0)=80m

Fig. 5 presents the results obtained in the above three scenarios, comparing simulation results with those obtained by our two approximations for the probability that a multihop path is available. We observe that both approximations are satisfactory when the probability of path availability is not too low. Indeed, the use of the refined approximation that partially accounts for link correlation does not provide significant improvements with respect to the one based on the independence assumption.

D. Performance Evaluation

We show how our analysis can be exploited to improve the efficiency of traffic routing in MANETs. In particular show how to select the optimal route in terms of path availability and how to determine the optimal number of hops between source and destination, taking into account the initial distance between the nodes. We then propose an approach to find and select routes, which accounts for the expected data transfer time over the path and allows to reduce the overhead of reactive routing protocols.

Knowledge of the variance of the spatial distribution has enabled us to derive an approximate expression of the probability of link availability. The approximation relies on the observation that the total movement of a node with respect to its initial position is determined by the sum of its elementary movements. The central limit theorem can therefore be invoked to claim that after some time the node spatial distribution tends to become a normal distribution. Hence, we have plugged into (12) a normal distribution with variance given by (11). A similar approximation can be applied to obtain the link duration probability.

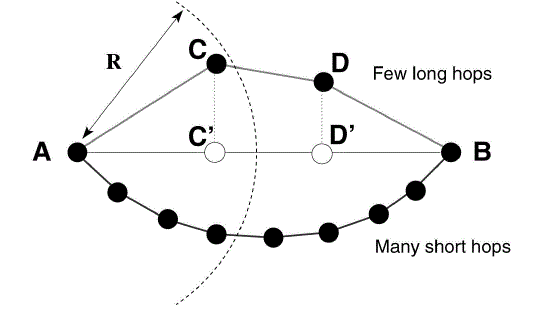
In the following discussion, we assume that the parameters of the underlying mobility model of the nodes are given (e.g., obtained through measurements) and that all nodes have a fixed, common radio range R. To introduce the problem of path selection, suppose node A wants to communicate with node B (see Fig. 6), possibly using intermediate nodes as relays. To maximize the stability of the route in response to node mobility, one can think of two different strategies: 1) a few long hops and 2) many short

hops. On the one hand, considering that the entire path fails if just a single link fails and that nodes move independently of each other, it seems better to minimize the number of hops. On the other hand, short links are much more stable than long links (see Fig. 6).

IV. CONCLUSION

In this paper, we studied the duration and availability probabilities of routing paths in MANETs—a fundamental issue to provide reliable routes and short route disruption times. We focused on the Random Direction mobility model and derived both exact and approximate (but simple) expressions for the probability of path duration and availability. We used these results to determine the optimal path in terms of route stability; in particular, we showed some properties of the optimal path and we provided an approximate yet accurate expression for the optimal number of hops. Finally, based on our findings, we proposed an approach to find and select routes, which accounts for the expected data transfer time over the path and allows to reduce the overhead of reactive routing protocols. In future we suggest to use this technology in communication field to avoid the traffic and over packet loss as replace for current using technology. Because of maintenance cost of this technology is very low compare to the current using method that is economically this method became cheap and also results are very accurate.

Figures at a glance


Figure 1	Figure 2	Figure 3

Figure 4	Figure 5	Figure 6

References

Christian Bettstetter, Giovanni Resta, and Paolo Santi, “The Node Distribution of the RandomWaypoint Mobility Model for Wireless Ad Hoc Networks," IEEE Transaction on MobileComputing, Vol.2, pp.257-269 July-Sept.2003.

Yu-Chee Tseng, Yueh-Feng Li, and Yu-Chia Chang, “On Route Lifetime in Multihop MobileAd Hoc Networks," IEEE Transaction on Mobile computing, vol.2, pp.366-376, Oct-Dec. 2003.

Fan Bai, Narayanan Sadagopan, Bhaskar Krishnamachari, and Ahmed Helmy, “ModelingPath Duration Distributions in MANETs and Their Impact on Reactive Routing Protocols," IEEE J.selected areas comm.., vol. 22, no. 7, pp. 1357-1373, Sept. 2004.

Sungsoon Cho and John P. Hayes, “Impact of Mobility on Connection Stability in Ad HocNetworks,” Proc. IEEE Wireless comm. and Networking conf. (WCNC ‘05), PP. 1650-1656, Mar.2005.

Michele Garetto, and Emilio Leonardi, “Analysis of Random Mobility Models with PartialDifferential Equations ,” IEEE Transaction on Mobile Computing, vol. 6, no. 11, pp.1204-1217,Nov. 2007.

T. Spyropoulos, K. Psounis, and C.S. Raghavendra, “Performance Analysis of MobilityassistedRouting ,” Proc. ACM MobiHoc, pp. 49-60, May 2006

Douglas S. J. De Couto, Daniel Aguayo, John Bicket, Robert Morris , “A High ThroughputPath Metric for MultiHop Wireless Routing ,” Proc. ACM Mobile Computing, Sept. 2003.

Prince Samar and Stephen B. Wicker , “On the Behavior of Communication Links of a Node ina Multi-Hop Mobile Environment ”, Proc. ACM MobiHoc, pp. 145-156, May 2004.

Richard J. La, and Yijie Han “Distribution of Path Durations in Mobile Ad Hoc Networks andPath Selection ”, IEEE/ACM Transactions on Networking, Vol. 15, no. 5. pp. 993-1006, Oct 2007.