Research and Reviews - International Journals

International Journal of Innovative Research in Computer and Communication Engineering

Menu

ISSN ONLINE(2320-9801) PRINT (2320-9798)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Implementation of Digital Signal Processing Algorithm in General Purpose Graphics Processing Unit (GPGPU)

Jagdamb Behari Srivastava1, R.K. pandey2, Jitendra Jain3
  1. Programme Asst. (Computer), Jawaharlal Nehru Krishi Vishwavidyalaya , Jabalpur, India
  2. Dr. , Prof. & Head, UICSA, Rani Durgavati Vishwavidyalaya , Jabalpur, India
  3. Assistant Professor, Dept. of ECE, JUET College of Engineering, Guna, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Abstract

In this paper, we have proposed sequential and parallel matrix and matrix-vector multiplication in compute unified device architecture (CUDA) libraries. We show the process of a class of algorithms parallelization which are used in digital signal processing. We present this approach on the instance of the Linear Convolution, Circular Convolution, and Least Mean Square (LMS) algorithm. We propose an approach which uses a general purpose graphics processor unit (GPGPU) technology. The accelerated version on GPU computed faster because it took less time compare to the MATLAB and sequential implementation.

Keywords
Linear Convolution, Circular Convolution, Least Mean Square (LMS), Computed unified device architecture (CUDA).

INTRODUCTION
A graphics processing unit (GPU) provides a parallel architecture which combines raw computation power with programmability. The architecture of GPU offers a large degree of parallelism at a relatively low cost through the well know vector processing model know as Single Instruction, Multiple Data (SIMD) [1], [2]. A computer which exploit multiple data stream against a single instruction stream to perform operations which may be naturally parallelized. For example, array processor and GPU [3]. There are two types of processor used in GPU i.e. Vertex and Pixel (or fragment) processors. The programmable Vertex and Pixel processors execute a user defined assembly level program having 4-way SIMD instructions. The Vertex processor performs mathematical operations that transform a vertex into a screen position. This result is then pipelined to the Pixel or fragment processor, which performs the texturing operations [4]. GPU can only process independent Vertices and Pixels processor, but can process many of them in parallel.
In this sense, GPU are stream processors. Each element in the stream are applied function using kernels. There are many of algorithms uses in digital signal processing which need a strong computational power to work in real time. In many situations the most complex (from the computational point of view) part of these algorithms is problem of large matrix multiplication and matrix-vector multiplication. In this paper, primary focus has been given to the matrix multiplication and matrix-vector multiplication.
MATLAB is a high-level language and interactive computation environment that enables to user to perform computationally intensive tasks [5]. This paper presents the speed-up achieved and benefits of the CUDA accelerated version of Linear Convolution, Circular Convolution and Least Mean Square (LMS) algorithm.

II. MEMORY MANEGMENT
Global memory resides on the device, but off-chip from the multiprocessors, so that access times to global memory can be 100 times greater than to shared memory. All threads in the kernel have access to all data in global memory. Shared memory is comparable to L1 cache memory on a regular CPU
It resides close to the multiprocessor, and has very short access times. Shared memory is shared among all the threads of a given block. Thread-specific memory stored where global memory is stored. Variables are stored in a thread's local memory if the compiler decides that there are not enough registers to hold the thread's data. This memory is slow, even though it's called "local" [6].
The main problem in parallelization of existing algorithms on CUDA devices is appropriate use of memory. On NVIDIA Tesla architecture, a thread block has 16 kB of shared memory visible to all threads of the block. All threads have access to the same global memory. Global memory can be 100 times greater than to shared memory. When there is no bank conflicts accessing the shared memory are fast as accessing a register. For comparison access to the global memory takes 400 -600 cycles [7].

III. PARALLEL PROCESSING BASED ON CUDA
CUDA was introduced by NIVIDIA Company in November 2006. It is a general purpose parallel computing architecture with a new parallel programming model, and an instruction set architecture that leverages the parallel compute engine in NVIDIA GPU to solve many complex scientific computational problems in a more efficient way than on CPU [6]. The CUDA program model includes a host and one or more devices. The host’s execution unit is CPU which executes the serial program, because CPU has a strong power to do logic operation. And the device’s execution unit is GPU which executes the parallel program because GPU has many arithmetic logic units (ALU) processing at the same time. The program which executed in the device is called kernel which is executed N times in parallel by the different N CUDA threads. In CUDA program model, the thread is the least computed unit. The kernel is executed in each thread. A certain number of kernels can consist a block. The maximum number of kernel in a block is 512. Every thread in a block can share the shared memory in block.

IV. DIGITAL SIGNAL PROCESSING ALGORITHM
• Linear Convolution vs. Circular Convolution
Consider a finite duration sequence x(n) of length N1 which is given a input to an finite impulse response (FIR) system with impulse response h(n) of length N2, then the output is given by
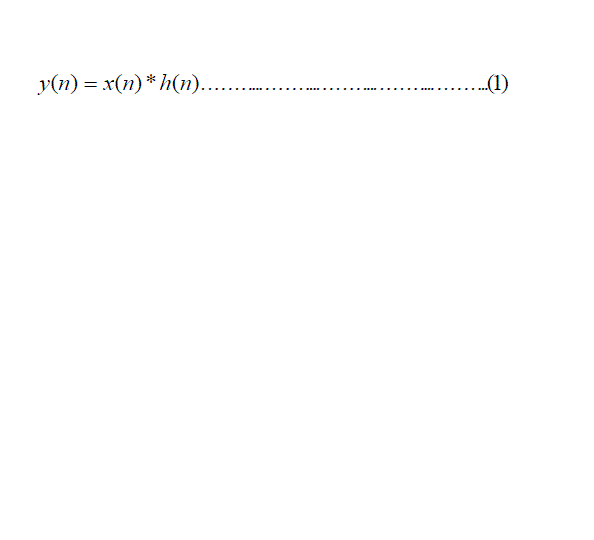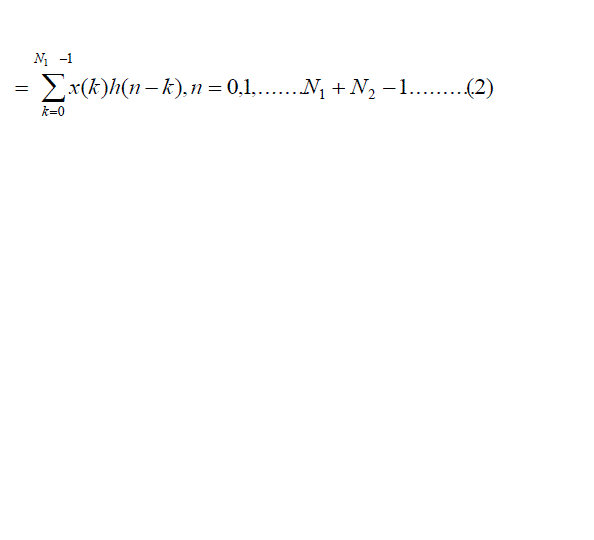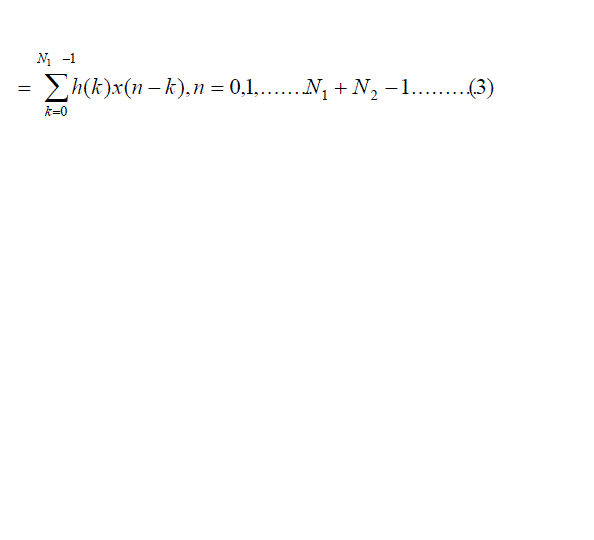Where,
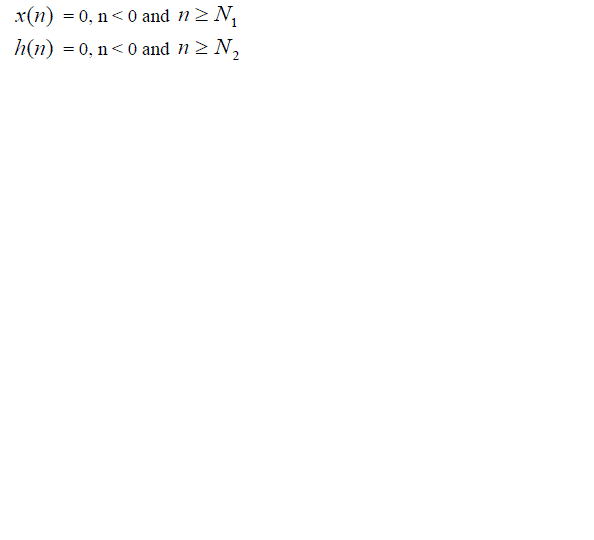The N-point circular convolution of x(n) with h(n) must be equivalent to the linear convolution of x(n) with h(n) . In general, the linear convolution of two sequences x(n) and h(n) with lengths N1 and N2 respectively will give a sequence with a length of N ≥ N1+ N2-1. When x(n) and h(n) have a duration less than N, for implementing linear convolution using circle convolution, N2 - 1 and N1 - 1 zeros are padded (added) at the end of x(n) an h(n) respectively to increase their length to N.
• Least Mean Square (LMS) Algorithm
We know that the most complex part of the LMS algorithm is matrix multiplication part [8]. The main advantage of LMS algorithm is that it requires simple computation. In practical applications of adaptive filtering, a fixed step size algorithm. In this filter we assume that a modification of h(n) vector of the h(n) filter parameter should be proportional in each time moment n to the cost function, gradient vector j(n) , which can be written an equation
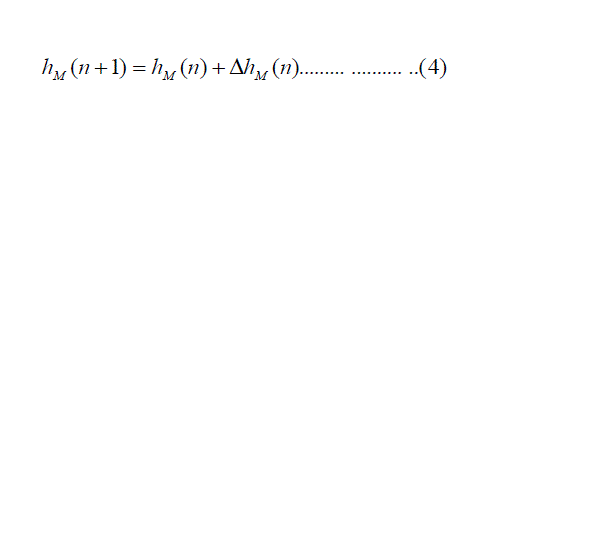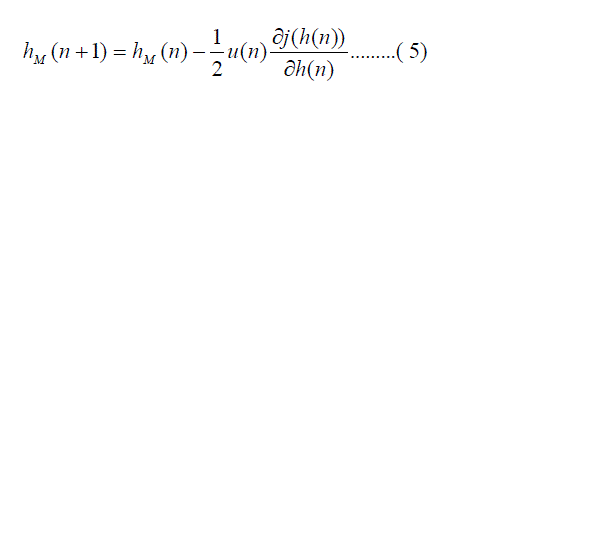Where u(n) is a scale variable which influences onto the speed of the filter modification. To speed up of the adaptation process, an additionally weight matrix is introduced. Such modified equation (5) takes the form of:
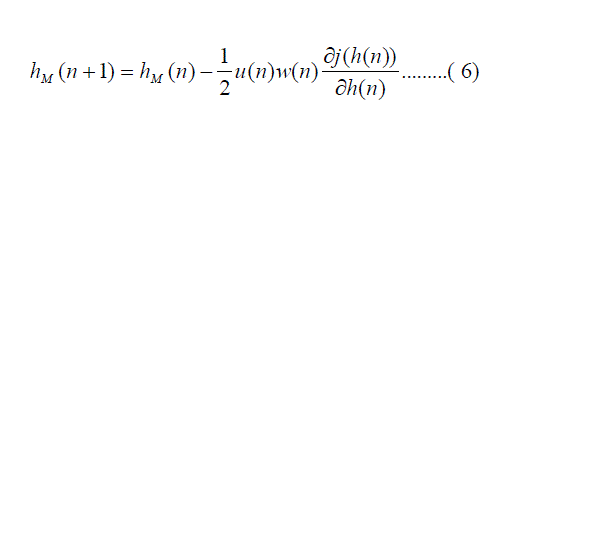In the case of LMS a temporal error value is minimized. Therefore the error criterion takes the form of :
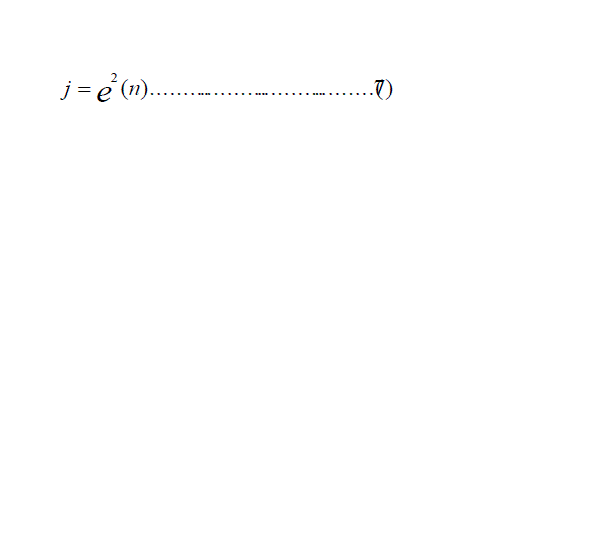Finally, the equation (4) takes the form of :
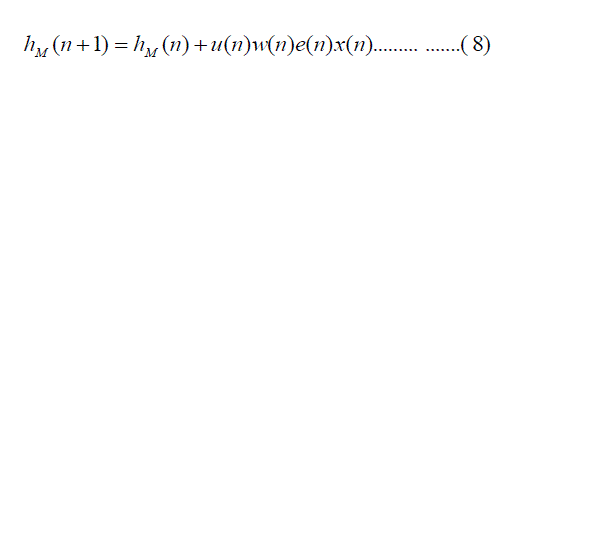This can be formulated in the matrix form as:

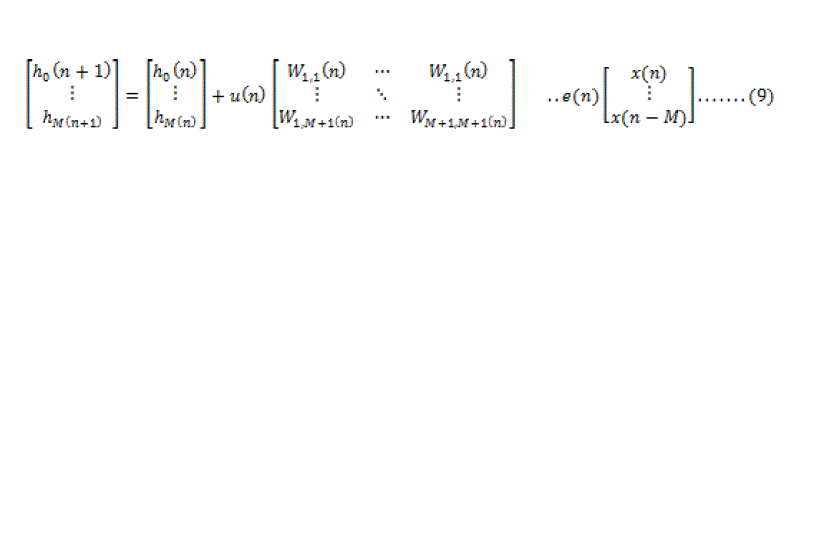V. GPU PROGRAMMING
The code was implemented in Microsoft Visual Studio 2010 (Express Edition) C with CUDA 5.0.
o Kernels
A kernel is the unit of work that the main program running on the host computer offloads to the GPU for computation on that device. In CUDA, launching a kernel requires specifying three things:
• The dimensions of the grid
• The dimensions of the blocks
• The kernel functions to run on the device.
The main matrix (square) code is presented below.
The main matrix vector code is presented below.

VI. SIMULATION RESULTS
There were two versions of algorithm sequential and parallel. Both of them was coded in C with using CUDA libraries and run on NVIDIA GeForce GT 630M with 2 GB dedicated VRAM (Video Random Access Memory) graphics card installed on Acer V3-571G, Intel Core i5-3210M 2.5GHz with Turbo Boost up to 3.1 GHz.
We have implemented of sequential matrix multiplication, sequential matrix-vector multiplication, parallel matrix multiplication and parallel matrix-vector multiplication for different matrix dimensions, shows the result in Table I and Table II respectively
The computation of MATLAB and CUDA together with GeForce GT 630M graphics card solved the day to day increasing demand for the massive parallel general purpose computing. The accelerated version on GPU was astonishingly fast, because it took less time compare to the MATLAB and sequential implementation. However, this value is strictly limited to the execution of computation kernel itself and doesn't include any overhead cost. Comparison between proposed implementation and Ing.et.al. [9]for an dimensional matrix multiplication, show the result in Table III.

VII. CONCLUSIONS
In this paper, we implemented and studied the performance of computing the absolute difference using matrix multiplication and matrix-vector multiplication. It has been shown that proposed GPU implementation better than other GPU, MATLAB, sequential implementation. We have shown that GPU is an excellent candidate for performing data intensive digital signal algorithms. A direct application of this work is to perform Linear Convolution, Circular Convolution and Least Mean Square (LMS) algorithm on GPU in real time digital signal processing.

Tables at a glance
Table icon Table icon Table icon
Table 1 Table 2 Table 3
 

Figures at a glance
Figure 1
Figure 1
 

References