ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
Mohamed I. A. Othman1,2 and Mohamed I. M. Hilal1
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
The present article deals with the gravity field and the laser pulse on porous thermoelastic solid under the effect of the temperature dependent properties in the context of the Green-Naghdi theory. The normal mode method used to obtain the exact solution of the considered physical quantities which have been shown graphically in the presence and the absence of the physical operators used in the problem
Keywords |
| Gravity, Green-Naghdi, Laser pulse, Normal mode, Porous, Temperature dependence, Thermoelasticity. |
INTRODUCTION |
| In the classical thermoelasticity (C-D) theory due to Biot [1], the equation of the heat conduction is a parabolic type. It could predict the infinite speed of the heat propagation in elastic media, but it was inconsistent with experimental observation. With this motivation, Lord and Shulman [2], and Green and Lindsay [3], established the (L-S) and (G-L) generalized thermoelasticity theories respectively. In the (L-S) theory, a relaxation time parameter introduced into the Fourier heat conduction equation, with the heat flux and its time derivative taken into account. The heat equation associated with this theory is essentially of a hyperbolic type. In the (G-L) theory, the constitutive equations were modified by introducing two relaxation time parameters. Both the equations of motion and heat conduction are of the hyperbolic type. The two theories can better characterize thermal disturbances with limited speed of the wave propagation and exhibit the so-called second sound effect in solids. Later, Green and Naghdi [4-6] established a new generalized thermoelasticity theory (G-N) theory of three types based on the energy and entropy balances, in which the energy dissipation was not considered in the previous theories. The linearized form of type I was equivalent to the classical thermoelasticity (C-D) theory. Type II describes the thermoelastic system without energy dissipation, while type III permits the dissipation of the energy. Therefore, the (G-N) theory is an ideal thermoelasticity theory. Ailawalia et al. [7] studied the effect of initial stress and rotation in (G-N) theory of type III. Othman et al. [8, 9] investigated the effect of rotation, the gravity and temperature dependent properties of porous thermoelastic solid with (G-N) theory. There are a number of theories about the mechanical properties of the porous materials. The concept of a distributed body introduced by Goodman and Cowin [10] in the context of granular and porous materials asserts that the mass density has the decomposition γ *φ where γ * is the density of the matrix material and φ is the volume fraction filed. This representation introduces an additional degree of kinematic freedom. Nunziato and Cowin [11] used this concept to present a non-linear theory to describe the properties of homogeneous elastic materials with voids free of fluid. Moreover, the theory of Cowin and Nunziato a more appropriated theory than other theories for the study of special continuum and geological materials, such as rocks, soils, and manufactured porous materials like ceramics and pressed powders. Generally, this theory based on the balance of energy, where the presence of the pores or voids involves an additional degree of freedom, called the fraction of elementary volume. In [12] Cowin and Nunziato established a theory to describe the linear elastic materials with voids. Iesan [13, 14] has developed a linear theory of thermoelastic materials with voids. The temperature dependence is an important physical property of materials reflecting the elastic deformation capacity of the material when subjected to an applied external load. Most of the investigations were done under the assumption of the temperature-independent material properties, which limit the applicability of the obtained solutions to certain ranges of temperature. At high temperature, the material characteristics such as the modulus of elasticity, Poisson's ratio, the coefficient of thermal expansion and the thermal conductivity are no longer constants [15]. In recent years due to the progress in various fields in science and technology the necessity of taking into consideration the real behaviour of the material characteristics prosperities as the temperature dependent measurements. In the classical theory of elasticity, the effect of the gravity neglected in a general manner. Bromwich [16] in particular on an elastic globe, was the first study the effect of the gravity of the problem of propagation of waves in solids. Laser at a high intensity when interacts with the solid surface, the absorption takes place. This in turn causes an internal energy gain of the substrate material and heat release from the irradiated region. Since the process, in general, is fast, the temperature gradients remain high in the irradiated region. This results in high thermal strain and thermally induced stresses in this region. The ultra-short lasers are those with the pulse duration ranging from nanoseconds to femto-seconds. In the case of ultra-short-pulsed laser heating, the high intensity, energy flux and ultrashort duration laser beam have introduced situations where very large thermal gradients or an ultra-high heating rate may exist on the boundaries by Sun et al. [17]. The microscopic two-step models, that is, parabolic and hyperbolic are useful for modifying the material as thin films. When a laser pulse heats a metal film, a thermoelastic wave generated due to thermal expansion near the surface. Othman et al. [18] investigated a model of thermoelasticity under thermal loading due to laser pulse. |
| This investigation studies the effect of the temperature dependent properties and the gravity field of porous thermoelastic solid heated by laser pulse with both types II and III of the (G-N) theory. The physical quantities obtained analytically. The physical quantities represented graphically in the presence and the absence of the gravity, the temperature dependent, the laser pulse and the porous effect. |
BASIC EQUATIONS, FORMULATION AND SOLUTION OF THE PROBLEM |
| Following Green and Naghdi [5] of type III, Cowin and Nunziato [12], the field equations and the constitutive relations for a porous linear homogenous, isotropic thermoelastic solid without body forces, heat sources and extrinsic equilibrated body force and heated by a laser pulse, can be written as |
 |
 |
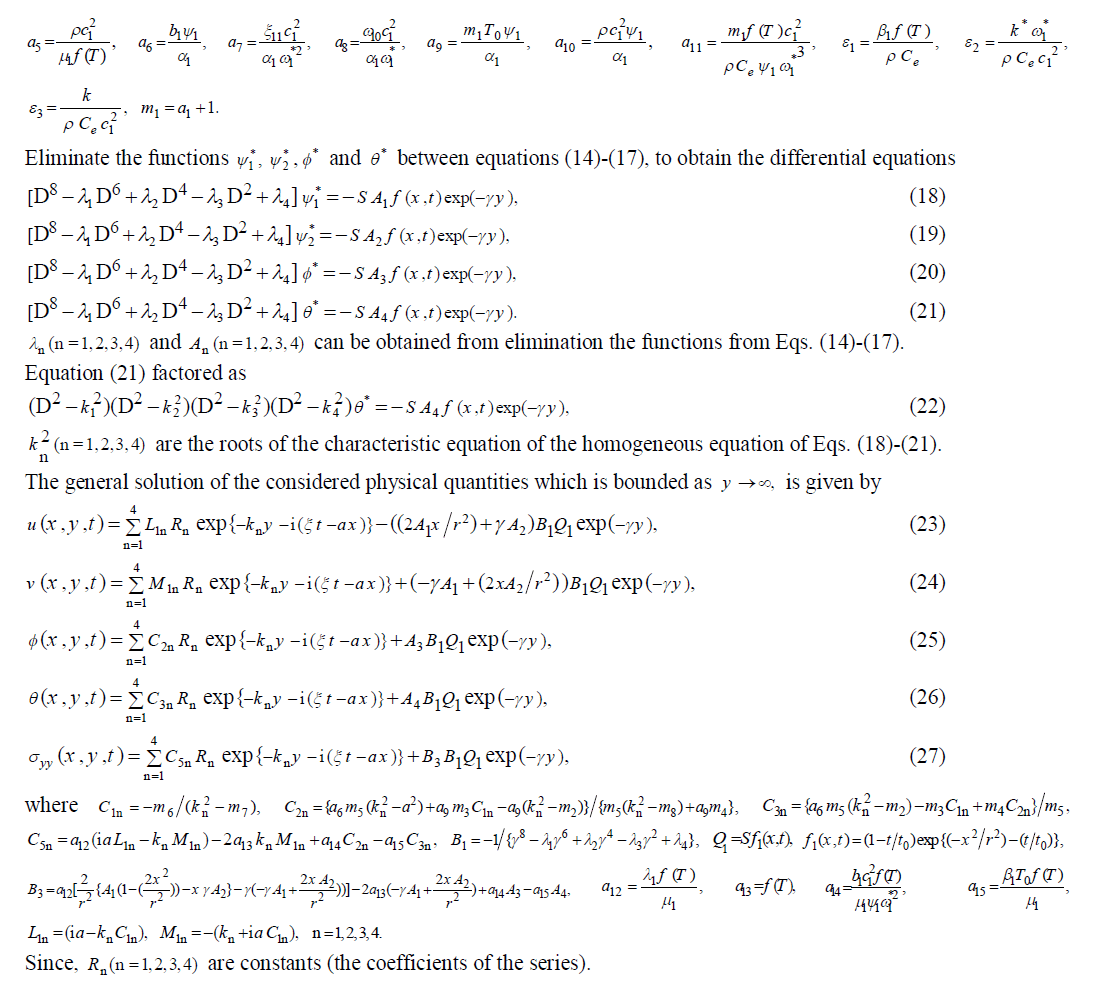 |
APPLICATIONS |
| Consider the following non-dimensional boundary conditions to determine the coefficients Rn (n = 1,2,3,4) and suppress the positive exponentials to avoid the unbounded solutions at infinity. Then the surface of the solid at y = 0 assumes these conditions |
| (1) The mechanical boundary conditions are |
| (i) The normal stress condition (mechanically stressed by constant force p1 ), so that |
 |
 |
| Hence, obtain the expressions for the physical quantities of the plate surface. |
PARTICULAR CASES |
| (i) In the case of absence of the gravity: taking g = 0 in equation (1). |
| (ii) In the case of absence of the temperature dependent properties: taking α* = 0 in the relations |
| (iii) In the case of the absence of the porous: taking |
NUMERICAL RESULTS AND DISCUSSION |
| Following Dhaliwal and Singh [19], the porous magnesium crystal-like thermoelastic solid chosen to evaluate the numerical results. All the units of parameters used in the calculation given in SI units. The constants of the problem taken as |
 |
 |
| Fig. 9 shows the variation of the displacement u in the case of the absence and the presence of the laser pulse effect; it noticed that the variation of u is increasing in both types II and III of (G-N) theory for y > 0 with the increase of the laser pulse value of the porous thermoelastic solid. Fig. 10 expresses the variation of σ yy in the case of the absence and the presence of the laser pulse effect; it observed that the variation of σ yy is increasing in both types II and III of (G-N) theory for y > 0 with the increase of the laser pulse value of the porous thermoelastic solid. |
 |
 |
CONCLUSIONS |
| The gravity and the temperature dependent properties have a significant effect on the variation of the considered physical quantities, since they make great changes in the behaviour of the functions, also the same observation of the absence and the presence of the porous and the laser pulse effect in the thermoelastic solid. The laser pulse heating effect is an important thermal loading in many scientific uses as the biological and the geological treatments of the materials. These physical quantities are continuous functions and all the curves converge to zero, as the solution using the normal mode method gives the exact solutions of the functions. |
References |
|