Research and Reviews - International Journals

International Journal of Innovative Research in Science, Engineering and Technology

Menu

ISSN ONLINE(2319-8753)PRINT(2347-6710)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Iterative Methods for Computing Eigen values and Eigen vectors with an Improved

Farnosh Izadi
Associate Professor, Islamic Azad University, Sowmesara Branch, Sowmesara, Iran
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Abstract

One of the oldest techniques for solving eigenvalue problems is the so-colled power method. In this study, we examine some numerical iterative methods for computing the eigenvalues and eigenvectors of real matrices. The two methods examined here range from the simple power iteration method, and we produced an improvement in the convergence of them. Our work is based on choosing of initial vector in iterative methods for acceleration purpose. Finally, some examples are presented to illustrate the method and results discussed.

Keywords
Aitken Acceleration, Power method, Rayleigh method, Dominant eigen value

INTRODUCTION
Eigenvalues and eigenvectors play an important part in the applications of linear algebra. The naive method of finding the eigenvalues of a matrix involves finding the roots of the characteristic polynomial of the matrix. In industrial sized matrices, however, this method is not feasible, and the eigenvalues must be obtained by other means. Fortunately, there exist several other techniques for finding eigenvalues and eigenvectors of a matrix, some of which fall under the realm of iterative methods. These methods work by repeatedly refining approximations to the eigenvectors or eigenvalues, and can be terminated whenever the approximations reach a suitable degree of accuracy. Iterative methods form the basis of much of modern day eigenvalue computation. In this paper, we outline two such iterative methods, and summarize their derivations, procedures, and advantages. The methods to be examined are the power iteration method and the Rayleigh quotient method.
This paper is meant to be an improvement of existing algorithms for the eigenvalue computation problem. Section 2 of this paper provides a brief review of some of the linear algebra background required and algorithms of two existing methods. In Section 3, we have presented us idea on the existing algorithms. In Section 4, have been produced 4 numerical examples. Finally, in Section 5, we summarized some remarks and mention some of the additional algorithm refinements that are used in practice. We restrict our attention to real-valued, square matrices with a full set of real eigenvalues.

ITERATIVE METHODS
Image
Image

NEW METHOD
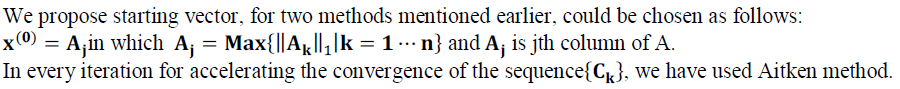Image

EXAMPLES
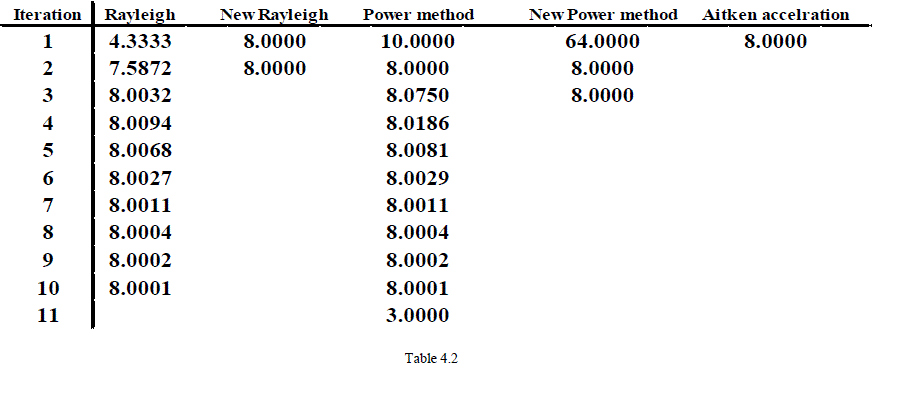
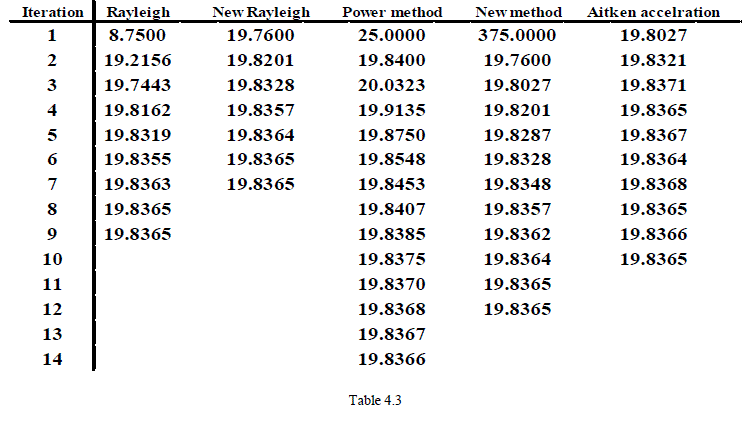
In this section, we consider three examples that we used eps =10-4 for all of them. All results have been computed using MATLAB [9].
Exp4.1 Let the following matrix of A with the largest eigenvalue of λ=3.
Image
Image

CONCLUSION
Here, we used the new initial vector for the two existing methods for the approximation of dominant eigenvalue. Then, we have used Aitken method for acceleration purpose. Numerical examples show the new method is faster.

References
  1. Moler, C. , Stewart, G. , “An Algorithm for Generalized Matrix Eigenvalue Problems”, SIAM J. Numer. Anal., Vol 10, No 2, 1973.
  2. Golub, G. H. , Van Loan, C. F., “Matrix Computations”, Johns Hopkins University Press, 1996.
  3. Stewart, G. W., “Introduction to Matrix Computations” , Academic Press, New York, 1973.
  4. Golub, H. G., Van Loan, C. F. , “Matrix computations” , Johns Hopkins University Press, Baltimore, 1996.
  5. Fraleigh, J. B., Beauregard, A. R. , “Linear algebra” , Addison-Wesley Publishing Company, 1995.
  6. Kaniel, S. , “Estimates for some computational techniques in linear algebra” , Math. Comp. Vol20 , pp. 369-378 , 1966.
  7. Peters, G. , Wilkinson, J. H. , “The calculation of specified eigenvectors by inverse iteration” , Contribution II/18in: Wilkinson and Reinsch, 1971.
  8. Peters, G. , Wilkinson, J. H. , “ Ax= Bx and the generalized eigenproblem” , SIAM J. Numer. Anal. , Vol 7, pp. 476-492, 1970.
  9. Store, J. ,Bulirsch, R. , “Introduction to Numerical Analysis” , Springer-Verlag, New York, 2002.
  10. Lecture 28: QR Algorithm, University of British Columbia CS 402 Lecture Notes, 1–13.
  11. Shores, Thomas, S. , “Applied linear algebra and matrix analysis”, Springer Science, 2007.
  12. Yang, W. Y. , Cao, W. , Chung, T. S. , Morris, J. , “Applied Numerical Methods sing MATLAB” , John Wiley & Sons Publication, New Jersey, 2005.