Keywords
|
| Convex optimization, multi-user wireless communication, multiple-input multiple-output (MIMO), orthogonal frequency-division multiplexing (OFDM), peak-to-average (power) ratio (PAR) reduction, pre coding |
INTRODUCTION
|
| Large-scale multiple-input multiple-output (MIMO) wireless communication is a promising means to meet the growing demands for higher throughput and improved quality-of-service of next-generation multi-user (MU) wireless communication systems. The vision is that a large number of antennas at the base-station (BS) would serve a large number of users concurrently and in the same frequency band, but with the number of BS antennas being much larger than the number of users, say a hundred antennas serving ten users. Large-scale MIMO systems also have the potential to reduce the operational power consumption at the transmitter and enable the use of low-complexity schemes for suppressing MU interference (MUI). All these properties render large-scale MIMO a promising technology for nextgeneration wireless communication systems. |
| While the theoretical aspects of large-scale MU-MIMO systems have gained significant attention in the research community, much less is known about practical transmission schemes. As pointed out in practical realizations of largescale MIMO systems will require the use of low cost and low-power radio-frequency (RF) components. To this end, reference proposed a novel MU pre coding scheme for frequency-flat channels, which relies on per-antenna constant envelope (CE) transmission to enable efficient implementation using non-linear RF components. Moreover, the CE pre coder of forces the peak-to-average (power) ratio (PAR) to unity, which is not necessarily optimal as in practice there is always a trade-off between PAR, error-rate performance, and power amplifier efficiency. |
| Practical wireless channels typically exhibit frequency selective fading and a low-PAR pre coding solution suitable for such channels would be desirable. Preferably, the solution should be such that the complexity required in each (mobile) terminal is small (due to stringent area and power constraints),where as heavier processing could be afforded at the BS. Orthogonal frequency-division multiplexing (OFDM) is an efficient and well-established way of dealing with frequency selective channels. In addition to simplifying the equalization at the receiver, OFDM also facilitates per-tone power and bit allocation, scheduling in the frequency domain, and spectrum shaping. However, OFDM is known to suffer from a high PAR, which necessitates the use of linear RF components (e.g., power amplifiers) to avoid out-of-band radiation and signal distortions. Unfortunately, linear RF components are, in general, more costly and less power efficient than the iron-linear counterparts, which would eventually result in exorbitant costs for large-scale BS implementations having hundreds of antennas. Therefore, it is of paramount importance to reduce the PAR of OFDMbased large-scale MU-MIMO systems to facilitate corresponding low-cost and low-power BS implementations. |
| To combat the challenging linearity requirements of OFDM, a plethora of PAR-reduction schemes have been proposed for point-to-point single-antenna and MIMO wireless systems. For MU-MIMO systems, however, a straight forward adaptation of these schemes is non-trivial, mainly because MU systems require the removal of MUI using a precoder, PAR-reduction schemes suitable for the MU-MISO and MU-MIMO downlink were described and, respectively, and rely on Tomlinson-Harashima precoding. Both schemes, however, require specialized signal processing in the (mobile) terminals (e.g., modulo reduction), which prevents their use in conventional MIMO-OFDM systems, such as IEEE 802.11n or 3GPP LTE . |
FITRA: The (smallest) Lipschitz constant of the gradient 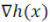 corresponds corresponds 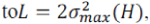 which can be calculated efficiently using the power method. To compute the proximal map for (P-INF-L), we define the auxiliary vector which can be calculated efficiently using the power method. To compute the proximal map for (P-INF-L), we define the auxiliary vector |
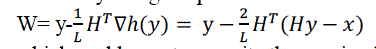 |
| which enables us to re-write the proximal map in more compact form as |
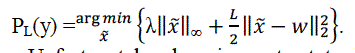 |
| Unfortunately, does in contrast to l1-norm regularized LS not have a simple closed-form solution for (P-INFL). Nevertheless, standard algebraic manipulations enable us to evaluate the proximal map efficiently using the following two step approach: First, we compute |
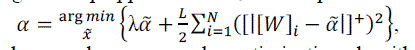 |
| for which general-purpose scalar optimization algorithms, such as the bisection method , can be used. |
Literature Survey:
|
| we present numerical simulation results to demonstrate the capabilities of the proposed MU-MIMO-OFDM downlink transmission scheme. Specifically, we analyze the trade-offs between PAR, error-rate performance, and out-of-band radiation, and we present a comparison with conventional pre coding schemes. In this implementation we have to compare with the scarcity signal with our PMP pre coding signal .such that we have say that PAR is again decreased by 2db by this l1 minimization of the signal. |
EXISTING METHOD
|
1)MIMO-OFDM:
|
| The growing demand of multimedia services and the growth of Internet related contents lead to increasing interest to high speed communications. The requirement for wide bandwidth and flexibility imposes the use of efficient transmission methods that would fit to the characteristics of wideband channels especially in wireless environment where the channel is very challenging. In wireless environment the signal is propagating from the transmitter to the receiver along number of different paths, collectively referred as multipath. While propagating the signal power drops of due to three effects: path loss, macroscopic fading and microscopic fading. Fading of the signal can be mitigated by different diversity techniques. To obtain diversity, the signal is transmitted through multiple (ideally) independent fading paths e.g. in time, frequency or space and combined constructively at the receiver. Multiple input- multiple-output (MIMO) exploits spatial diversity by having several transmit and receive antennas. However the paper “MIMO principles” assumed frequency flat fading MIMO channels. |
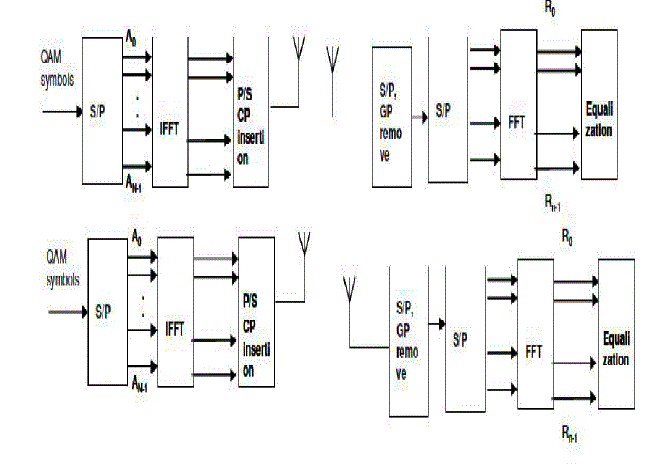
| OFDM is modulation method known for its capability to mitigate multipath. In OFDM the high speed data stream is divided into Nc narrowband data streams, Nc corresponding to the subcarriers or sub channels i.e. one OFDM symbol consists of N symbols modulated for example by QAM or PSK. As a result the symbol duration is N times longer than in a single carrier system with the same symbol rate. The symbol duration is made even longer by adding a cyclic prefix to each symbol. Aslong as the cyclic prefix is longer than the channel delay spread OFDM offers inter-symbol interference (ISI) free transmission. Another key advantage of OFDM is that it dramatically reduces equalization complexity by enabling equalization in the frequency domain. OFDM, implemented with IFFT at the transmitter and FFT at the receiver, converts the wideband signal, affected by frequency selective fading into N narrowband flat fading signals thus the equalization can be performed in the frequency domain by a scalar division carrier-wise with the subcarrier related channel coefficients. The channel should be known or learned at the receiver. The combination MIMO-OFDM is very natural and beneficial since OFDM enables support of more antennas and larger bandwidths since it simplifies equalization dramatically in MIMO systems. MIMO-OFDM is under intensive investigation by researchers. This paper provides a general overview of this promising transmission technique.The general transceiver structure of MIMO-OFDM is presented in Fig.2. The system consists of N transmit antennas and M receive antennas. In this paper the cyclic prefix is assumed to be longer than the channel delay spread. The OFDM signal for each antenna is obtained by using inverse fast Fourier transform (IFFT) and can be detected by fast Fourier transform (FFT). The received MIMO-OFDM symbol of the n:th subcarrier and the m:th OFDM symbol of the i:th receive antenna after FFT can be written as where Aj[ n,m] is the transmitted data symbol on n:th carrier and m:th OFDM symbol, Wi[n,m] is the additive noise contribution at i:th receive antenna for the corresponding symbol in frequency domain and Hi,j[n,m] is the channel coefficient in the frequency domain between the j:th transmit antenna and the i:th receive antenna. The channel coefficients in frequency domain are obtained as linear combinations of the dispersive channel taps. |
2).PAPR
|
| A major problem of multicarrier systems is that they show great sensitivity to nonlinear distortions. In-band and outof- band interferences caused by nonlinear distortions degrade BER performance of the system and give rise to interference to adjacent frequency bands, respectively. At the transmitter, the high power amplifier (PA) is the main source of nonlinear distortions. Due to the fact that amplifier nonlinearity is amplitude dependent, the amplitude fluctuations of the input signal are of a concern. The peak-to-average power ratio (PAPR), which is defined as the ratio of the peak power of the signal to its average power, is a measure of the amplitude fluctuations of the signal. Any multicarrier signal with a large number of subcarriers may have a high PAPR due to occasional constructive addition of subcarriers.In OFDM, when the number of carriers is large, the central limit theorem holds and the time domain samples of the OFDM signal, sampled at Nyquist rate, are approximately zero-mean complex Gaussian random variables. The problem of this PAPR approximation is that it is derived for the Nyquist rate sampled version of a continuous signal. The continuous signal may have higher amplitude peaks than our maximum sample would imply and this analysis underestimates the distribution of the PAPR. It can also be noted that the Gaussian distribution has infinite values but the largest amplitude value of an OFDM [9]signal is only N times the average amplitude of the carriers thus the approximation does not hold very accurately on large amplitudes i.e. the shape of the PAPR distribution is does not follow Gaussian in the tails of the distribution. The Gaussian approximation is compared to a CCDF of a Nyquist rate sampled signal and to CCDF of an oversampled signal with oversampling factor 16. |
Example of PAPR reduction in MIMO-OFDM
|
| A number of techniques have been proposed to reduce PAPR and they can be divided in two kinds of approaches. In the first approach, PAPR reduction can be obtained with help of redundancy and the second one is to apply a correcting function to the signal to eliminate the high amplitude peaks. This is very simple approach but it causes interference. Adding redundancy does not cause any interference but it adds complexity of the transmitter and lowers the net transmission rate. Selective mapping (SLM) belongs to the first approach. In SLM, V statistically independent sequences are generated from the same information by multiplying with a certain vector and that sequence with the lowest PAPR is selected. The information of the vector used to generate the selected sequence has to be sent to the receiver. Detection of the signal depends also on the errors on the side information transmission. |
PROPOSED METHOD
|
1)Continuation strategies applicable to FITRA ALGORITHM
|
| Compressed Sensing is the name assigned to the idea of encoding a large sparse signal using a relatively small number of linear measurements, and minimizing the `1-norm (or its variants)in order to decode the signal. New results reported by Candes et al Donoho et al and others stimulated the current burst of research in this area. Applications of compressed sensing include compressive imaging , medical imaging, multisensory and distributed compressed sensing analog-to-information conversion , and missing data recovery . Compressed sensing is attractive for these and other potential applications because it reduces the number of measurements required to obtain a given amount of information. The trade-of is the addition of a non-trivial decoding process.CS channel estimation method concerns the sparse reconstruction problem of estimating an unknown sparse channel vector from an observed vector of measurements R∈CM based on the linear model, namely the measurement by omitting the superscript for brevity. R=ψh+Z’ where ψ is a known measurement matrix, Z' is the measurement noise vector, and channel vector h is L sparse,where L is the number of multipath and is much |
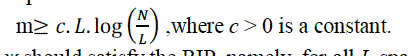 |
| Secondly, the measurement matrix ψ should satisfy the RIP, namely, for all L-sparse vector h, we have |
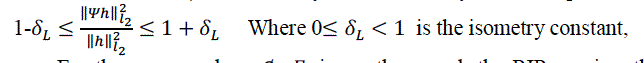 |
| ?.? is the l2-norm.For the concerned ψ=ømF in another word, the RIP requires the rows {øm,j} of m, φ cannot sparsely represent the column {Fi} of F and vice versa. Now we prove the RIP of the measurement matrix = m ψ φ F .As we mentioned above, mφ is the m-by-N matrix which consists of m unit vectors { } i e , and it is the unit matrix IN when the number of pilot m is N. F is the N-by-N DFT matrix, which is also the unitary matrix. Since I=FHF , every row of I, can be expressed as where is the conjugate operation, F is the (j, i)- th element of DFT matrix F , and F is the j-th column vector of F. Clearly the motivation to use compressive sensing in channel estimation is the observation that some channels are characterized by sparse multipath by that we mean that there are much fewer distinct arrivals as there are baseband channel taps. With this in mind compressive sensing promises to estimate the channel with much less pilot over head or at higher accuracy with a constant number of pilots. The common assumption is that a sparse multipath channel leads to a baseband channel model where most taps are negligible .We take a closer look at this and find that in a channel modeled by seculars (point) scatterers the number of nonzero baseband taps depends very much on what one defines as negligible .Using instead an oversampled baseband model ,the representation of the channel becomes ambiguous, but also more sparse. |
SIMULATION RESULTS FOR FITRA
|
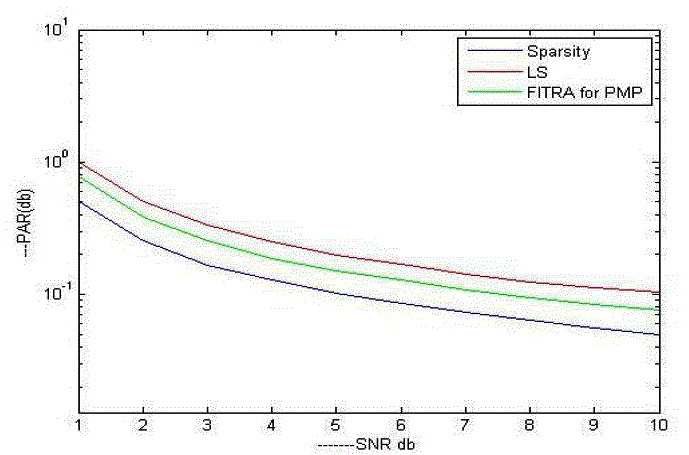
| Description: The figure 4-9 shows that comparison of PAR for scarcity, LS,PMP Signals .From these we have observed that scarcity achieves the LOW PAR Compared to all other .From this l1 minimization we have to get this sparse signal with low par. |
CONCLUSION AND FUTURE SCOPE
|
| The proposed joint pre coding, modulation, and PAR reduction framework, referred to as PMP, facilitates an explicit trade-off between PAR, SNR performance, and out-of-band interference for the large-scale MU-MIMO-OFDM downlink. As for the constant-envelope pre coder, the fundamental motivation of PMP is the large number of DoF offered by systems where the number of BS antennas is much larger than thenumber of terminals (users). Essentially, the downlink channel matrix has a high-dimensional null-space, which enables usto design transmit signals with “hardware-friendly” properties, such as low PAR. In particular, PMP yields per-antenna constant-envelope OFDM signals in the large-antenna limit,i.e., for N ! 1. PMP is formulated as a convex optimization problem for which a novel efficient numerical technique, called the fast iterative truncation algorithm (FITRA), was devised. Finally, further reducing the computational complexity of FITRA, e.g using continuation strategies like L1 minimization is vital for a practical realization of PMP in hardware.This is substantial benefits of compressive sensing for underwater acoustic Communications over long dispersive channels with large Doppler spread. |
| |
Figures at a glance
|
 |
 |
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
Figure 4 |
Figure 5 |
|
| |
References
|
- D. Do no ho, “Compressed sensing,” IEEE Trans. Info. Theory, vol. 52, no. 64, pp. 1289-1306, 2006
- E. J. Can des, “Compressive sampling,” in Proc. Int. Congress of Mathematics , Madrid, Spain, vol. 3, pp.1433-1452, 2006.[3] E. J. Can des and
- T. Tao, “Near optimal signal recovery form random projections: universal encoding strategies?,” IEEE Trans. Info. Theory, vol. 52, no. 12, pp. 5406-5425, 2006.
- S. F. Cotter and B. D. Rao, “Sparse channel estimation via matching pursuit with application to equalization,” IEEE Trans. Comm., vol. 50, no. 3, pp. 374-377, 2002.
- W. Li and J. C. Preisig, “Estimation of rapidly time-varying sparse channels,” IEEE J. Oceanic Eng., vol. 32, no. 10, pp. 927-939, 2007.
- W. U. Bajwa, A. M. Sayeed, and R. Nowak, “Learning sparse doublyselective channels,” in Proc. 46th Annu. Allerton Conf. Communication, Control, and Computing, Monticello, IL, USA, Sept. 2008.
- W. U. Bajwa, J. Haupt, G. Raz, and R. Nowak,, “Compressed channel sensing,” in Proc. 42th Annu. Conf. Information Sciences and Systems (CISS’08), Princeton, USA, pp. 5-10, 2008.
- G. Taubock and F. Hlawatsch, “A compressed sensing technique for OFDM channel estimation in mobile environments: exploiting channel sparsity for reducing pilots,” in Proc. ICASSP’08, Las Vegas, USA, pp. 2885-2888, 2008.
- M. R. Raghavendra and K. Giridhar, “Improving channel estimation in OFDM systems for sparse multipath channels,” IEEE Signal Proc. Lett.,vol. 12, no. 1, pp. 52-55, 2005.
- T. Kang and R. A. Iltis, “Matching pursuits channel estimation for an underwater acoustic OFDM modem,” in Proc. IEEE ICASSP’08, Las Vegas, USA, pp. 5296-5299, 2008.
- G. Taubock, F. Hlawatsch, and H. Rauhut, “Compressive estimation of doubly selective channels: exploiting channel sparsity to improve spectral efficiency in multicarrier transmission,” IEEE J. Select. Topics in Signal Process., vol. 4, no. 2, pp. 255-271, 2010.
- W. U. Bajwa, J. Haupt, and R. Nowak, “Compressed sensing of wireless channels in time, frequency, and space,” in Proc. 42th Asiomar Conf. Signals, Systems, and computes, Pacific Grove, Canada, Oct., 2008
|