International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Menu

ISSN ONLINE(2320-9801) PRINT (2320-9798)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Maintaining Privacy and Secrecy in Untrusted Network with Stile

M. Anbu Chezhian, S.Ramalakhsmi
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Abstract

Security and privacy issues have become critically important with the fast expansion of multi-agent systems. Most network applications such as pervasive computing, grid computing, and P2P networks can be viewed as multi-agent systems. sTile, a technique is proposed for distributing trust-needing computation onto insecure network systems which are open, anonymous, and dynamic in nature. sTile based implementation and empirically evaluate it on several physical networks of varying sizes, including the globally distributed system. Secure multiparty computational algorithm is used to ensure crystal neighbours do not learn each other’s data. Multifactor authentication process is proposed to provide security in the untrusted network.

Keywords
Privacy, Untrusted Network, sTile, Tile assembly model.

INTRODUCTION
The emergence of cloud computing is evolving the nature of computation. Instead of using private machines, users allow the cloud to maintain, manipulate, and safeguard their data. This evolution has allowed ubiquitous access to computation and data with higher availability and reliability than possible with personal machines and local servers. Simultaneously, this evolution has affected the meaning of the term privacy when referring to software systems. To ensure data remain private, not only must they be kept confidential from potential intruders, but also from the machines that execute computation on the data.

MOTIVATING EXAMPLE: ADDITION
To describe adding using sTile, we explain three separate elements of our solution: the addition tile assembly, the distribution process, and the source of privacy.
A. The Addition Tile Assembly
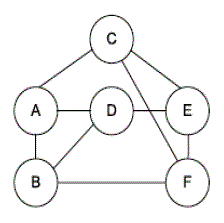
A tile assembly is a theoretical construct, similar to cellular automata. It consists of square tiles with static labels on their four sides. In Fig.1. Tiles can attach to one another or to a growing crystal of other tiles when sufficiently many of their sides match.
B. The Distribution Process
sTile uses the theoretical tile assembly to decompose a computation into small parts. Each small part represents a tile execution might be deployed on eight network nodes. Each node only deploys tiles of a single type, designated by the client machine. The client sets up a seed on the network by asking nodes that can deploy tiles of appropriate types to deploy instances of those types. Each node knows only the tile instances it is deploying and maintains references to the geometrically adjacent tile instances on other nodes. Next, tiles with an empty adjacent location coordinate with their crystal neighbour’s to recruit matching tiles to attach this process uses a secure multiparty computation algorithm to ensure crystal neighbour’s do not learn each other’s data. Each of these steps replies on an algorithm that ensures the tiles are deployed uniformly randomly on the available nodes. Once the execution finishes, the tiles in the middle row report the solution to the client, indicating the node IDs of their crystal neighbour’s, which the client uses to reconstruct the output.
C. The Source of Privacy
Each tile instance is aware of only a single bit of the input, output, or intra computation data, and not of the bit’s global location. An adversary may attempt to reconstruct the confidential data from the nodes it controls. For example, Fig. 1f shows an adversary that has compromised three nodes (2, 3, and 6), and now has access to the data in five tiles. However, this adversary can only tell that there are some 0 and 1 bits scattered throughout the input, the computation, and the output, but not how many and not their relative positions.

STILE ARCHITECTURE AND ALGORITHMS
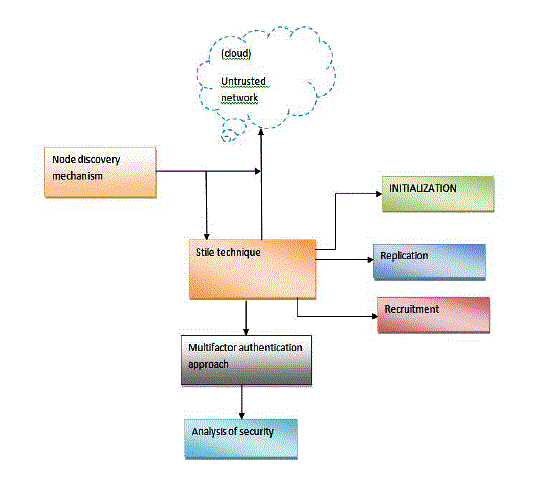
A sTile-based system is a software system that uses a network of computers to solve a computational problem. Intuitively, the network simulates a tile assembly: Each computer pretends to be a tile (or many tiles), and communicates with other computers to self-assemble a solution to a computational problem. Each computer deploys tile components, each representing a tile in a tile assembly, and facilitates the proper communication channels and algorithms to allow the tile component self-assembly. Thus, a tile architecture is based on a tile assembly; the software system employing that architecture solves the particular computational problem that the tile assembly solves.
A. Initializing Computation
The client computer initializes the computation by performing three actions: creating the tile type map, distributing the map and tile type descriptions, and setting up a seed crystal.
Creating the tile type map. A tile type map is a mapping from a large set of numbers (e.g., all 128-bit IP addresses) to tile types. It determines the type of tile components a computer with a given unique identifier (e.g., IP or MAC address) deploys. The tile type map breaks up the set of numbers into k roughly equal-sized regions, where k is the number of types of tiles in the tile assembly.
Distributing the map and tile descriptions. The client node distributes the tile type map and a short description of one tile type to a node that deploy that type, as determined by the tile type map. A tile type’s description consists of the four tile component interfaces, which can be described using a few bits.
Creating a seed. The client is responsible for creating the first seed on the network through a fairly straightforward procedure. For each tile in the seed crystal described by the underlying tile assembly, the client selects a node that deploys that tile type and asks that node to deploy a tile.
B. Discovery
The node discovery algorithm is central to sTile because initialization, replication, and recruitment all use it. The discovery operation, given a tile type, returns a uniformly random IP of some computer deploying tile components of that type. In Fig.2. Thus, every suitable computer has an equal chance of being returned, in the long run, which in turn guarantees that all nodes on the network perform a similar amount of computation. The algorithm uses a property of random walks to ensure uniform-randomness.
C. Recruitment
The seed crystal grows into a full assembly by recruiting tile attachments. In a computational tile assembly (such as the assembly described in that solves 3-SAT), a tile component that has both an upper and a left crystal neighbor recruits a new tile to attach to its upper left. Fig. 3 indicates several places in a sample crystal where tile components are ready to recruit new tiles. A recruiting tile component X (highlighted in Fig. 3), for each tile type, picks a potential attachment node Y of that type from its node table, as described in Section III, and sends it an attachment request.
D. Replication
Whenever network nodes have extra cycles they are not using for recruitment, they replicate the seed. Each node X uses its node table, as described in Section III, to find another node Y on the network that deploys the same type components as itself, and sends it a replication request. A replication request consists of up to two IP addresses (two 128-bit numbers) of X’s crystal neighbors. X lets its crystal neighbors know that Y is X’s replica (by sending Y ’s IP to X’s crystal neighbors). Those crystal neighbors, when they replicate using this exact mechanism, will send their replicas’ IPs to Y . Thus, the entire seed replicates. Each component’s replication is thus a three-step process: X sends a replication request to Y , Y replies to X, and X tells its crystal neighbors about Y . We analyze these steps in Section IV.
E. Solution Reporting
One tile type, the black tile in Figs. 3 and 4e, includes in its encoding the identity (IP address) of the client. Recall that the black tile only attaches to a crystal when that crystal finds a solution. When that happens, the node deploying the black tile informs the client that the Boolean formula is satisfiable. While 3-SAT is a decision problem (i.e., the answer is either “yes” or “no”), the client may wish to also learn the Boolean assignment that satisfies the formula. To do so, the client may ask the node that notified it of the solution for its crystal neighbors’ identities (IP addresses), and those for their crystal neighbors’ identities, to reconstruct the entire crystal responsible for finding the solution. The client can then query the nodes that deploy the tiles encoding the assignment for their tile types. The cost of reconstructing the entire crystal is no more than contacting, and getting a response from each of the nodes deploying tiles in that crystal (310 tiles for the 3-SAT example from Fig. 4). However, since only part of the crystal is responsible for the assignment, it can be retrieved even more efficiently. To ensure privacy, all the relevant communication must be encrypted, and each involved node must verify the identity of the client. These requirements can be handled using standard public key encryption and authentication techniques, which we do not describe here.

COMPUTATIONAL FEASIBILITY
To demonstrate that sTile is a feasible solution for building software systems that distribute computationally intensive problems on very large networks, we must show that 1) such systems’ computational speed is proportional to the size of the underlying network, 2) such systems are robust to network delay, and 3) real-world-sized problems can be solved on real-world-sized networks in reasonable time.
A. sTile-Based Implementations
We have built and made public two Mahjong-based implementations, for 3-SAT and Subset Sum, as well as Simjong-based simulations of the same systems. Simjong is a Java-based discrete-event simulator with network-delay simulation capabilities. Simjong executes on a single machine and creates a user-specified number of virtual hardware Node components, each capable of deploying tiles. Simjong’s network model allows for message delivery time to be constant, chosen at random from some distribution, or proportional to the geographic distance between locations assigned to each virtual node. Simjong’s network model is based on ns-2, simplified to abstract away the exact topology of the network.
B. Experimental Setup
We use three distributed networks for our experimental evaluation: 1) a private heterogeneous cluster of 11 Pentium 4 1.5-GHz nodes with 512 MB of RAM, running Windows XP or 2000; 2) a 186-node subset of USC’s Pentium 4 Xeon 3-GHz High Performance Computing and Communications cluster; and 3) a 100-node subset of PlanetLab, a globally distributed network of machines of varying speeds and resources that were often heavily loaded by several experiments at a time.
Our experimental goals were to verify sTile’s scalability with respect to network size and robustness to network delay. Our experiments had three independent variables the number of nodes, the network communication speed between nodes, and the size of the NP-complete problem and one dependent variable the time the computation took to complete.
C. Scalability
To verify that the speed of the computation is proportional to the number of nodes on the underlying network, for each of the three networks described above, we deployed Mahjong-based implementations on the entire network and on randomly selected halves of the network. We varied the size of the problem and measured the average time in which the implementations found the solution over 20 executions (except on PlanetLab, as explained above). We then also deployed Simjong on virtual networks of increasing size from 125,000 to 1,000,000 nodes (with a constant network delay of 100 ms for all packets).
D. Robustness to Network Latency
Intuitively, high-network latency should adversely affect the speed of sTile-based systems: If the tile attachments happen sequentially, the latency affects every attachment and greatly slows down the overall computation. This intuition holds for the addition example from Section 2. However, in the case of NP-complete computations, this intuition is false. In such computations, many of the sub computations (tile attachments) happen independently[7][9], in parallel. Each node in our experiments deployed millions of lightweight tiles, and whenever a sTile packet traveled between nodes, those nodes handled other tiles rather than waiting idly for the network communication to arrive. As a result, the throughput of sTile-based systems is not affected by the network latency.
E. Efficiency
The final claim we address in demonstrating sTile’s feasibility for industrial systems is that real-world-sized problems can be solved on real-world-sized networks in reasonable time. In particular, we posit that sTile-based systems can outperform existing privacy-preserving methods for solving NP-complete problems[12][14]. There are three ways to solve a highly parallelizable problem while preserving the data privacy: 1) on a large insecure network by using sTile, 2) on a single private computer, or 3) on a private network of trustworthy computers. We will first discuss the time needed to solve such a problem using the three methods in terms of the number of required operations, and then discuss the actual time necessary to solve problems.
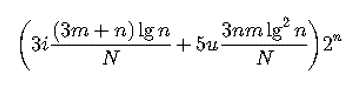equation (1)
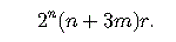equation (2)
Now, suppose a user wishes to solve the 3-SAT instance on a single computer. That computer would need to examine 2n possible assignments, and check each n-variable assignment against the m clauses. Equation (2) describes the time this procedure would take using the most efficient available technique, assuming r is the amount of time each operation takes to execute: For each assignment, create a hash set containing the n literal-selection elements and check for each of the 3m literals whether the hash set contains that literal.

PRIVACY PRESERVATION
In this section, we formally argue that sTile systems preserve privacy. Specifically, we analytically argue that, as long as no adversary controls more than half the network, the probability of that adversary learning the input can be made arbitrarily low.
sTile’s privacy preservation comes from each tile being exposed only to a few intermediate bits of the computation (see Fig. 4) and the tiles’ lack of awareness of their global position. To learn meaningful portions of the data, an adversary needs to control multiple, adjacent tiles. We call a distributed software system privacy preserving if, with high probability, a randomly chosen group of nodes smaller than half of the network cannot discover the entire input to the computational problem the system is solving[15][17]. (We will also discuss, at the end of this section, the probability of discovering parts of the input.) We argue that neither 1) a node deploying a single tile, nor 2) a node deploying multiple tiles can know virtually any information about the input; moreover, 3) controlling enough computers to learn the entire input is prohibitively hard on large networks.

RELATED WORK
Distributing computation. The growth of the Internet has made it possible to use public computers to distribute computation to willing hosts. This notion focuses the underpinning of computational grids. Among systems that concentrate on distributed computation are BOINC systems (such as SETI@home and Folding@home ), MapReduce , and the organic grid. A unique approach—FoldIt—uses the competitive human nature to solve the protein-folding problem[11]. These systems try to solve exactly the highly parallelizable problems toward which our work is geared, but unlike sTile, they do not preserve privacy.
Cloud privacy. Cloud computing has reemphasized the importance of data privacy[3][6], causing the emergence of numerous approaches for keeping data private on the cloud. Most such approaches concentrate on private data storage and user-authorized data retrieval and require some trusted agents whereas our work concentrates on preserving privacy during computation and requires no trusted agents.
Privacy-preserving computation. In classical (as opposed to quantum) computing, it is not possible to get help from a single entity in solving an NP-complete problem without disclosing most of the information about the input and the problem one is trying to solve[14]. Our approach avoids this shortcoming by distributing such a request over many machines without disclosing the entire problem to any small-enough subset of them.

CONCLUSION
sTile distributes computation onto large, insecure, public networks in a manner that ensures privacy preservation, fault and adversary tolerance, and scalability. We presented a rigorous theoretical analysis of sTile and formally proved that the resulting systems are efficient and scalable, and that they preserve privacy as long as no adversary controls half of the public network.
We deployed two sTile implementations on several networks, including the globally distributed PlanetLab [36], to empirically verify
1. the correctness of sTile algorithms,
2. that the speed of sTile computation is proportional to the number of nodes,
3. that network delay has a negligible effect on the speed of the computation, and
4. that our mathematical analysis of the time needed to solve large problems on large networks is accurate. For networks larger than about 4,000 nodes, sTile outperforms optimized solutions that assume privately owned, secure hardware.
sTile explores the fundamental cost of achieving privacy through data distribution and bounds the extent to which a privacy-preserving system is less efficient than a nonprivate one. While that cost is not trivial, we have demonstrated that sTile-based systems execute orders of magnitude faster than homomorphic encryption systems, the alternative promising approach to preserving privacy.

ACKNOWLEDGEMENT
The authors thank Jae young Bang for his help deploying Mahjong-based implementations on PlanetLab. This material was based upon work supported by the US National Science Foundation (grant 0937060 to the Computing Research Association for the CIFellows Project and grants 0905665 and 1117593), and by Infosys.

Tables at a glance
Table icon Table icon
Table 1 Table 2
 

Figures at a glance
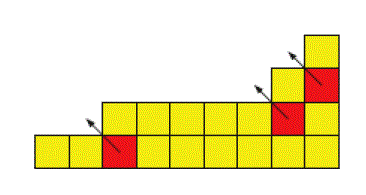Figure 1 Figure 2 Figure 3 Figure 4 Figure 5
Figure 1 Figure 2 Figure 3 Figure 4 Figure 5
 

References