Keywords
|
| Time series, periodicity detection, suffix tree, symbol periodicity, segment periodicity, sequence periodicity, noise resilient. |
INTRODUCTION
|
| The main Objective of this Project is creating an algorithm called “Efficient Mining of Partial Periodic Patterns in Time Series Database” which detects all 3 types Symbol, Sequence, Segment periodicity patterns in Time Series Database by using suffix tree as underlying data structure. And gives accurate result at all situations like insertion,deletion, replacement or mixture of all types of noise, proving that the creating algorithm is noise resilient. |
| The intended project detects: |
| • Frequent periodic patterns(of any length, any period satisfying the minimum support & confidence threshold) |
| • Periodicity in subsections of a series |
| • Periodicity in presence of noise(for replacement, insertion, deletion &any mixture of these three types of noise) |
| • Non-redundant periods |
| • Surprising or outlier periodic patterns Periodicity in non-uniformly sampled series Periodicity in larger series(Using data structure) |
RELATED WORK
|
| Existing periodic pattern detection algorithms are based on type of periodicity they detect like symbol, sequence, segment and based on detecting on whole time series or a subsection of the time series .Infominer is an algorithm which is used to check the time series for corresponding periodic patterns. Conv Is an algorithm, detects symbol, sequence periodicity and WARP is the advanced technique of Conv which detects segment Periodicity. ParPer is another algorithm which detects periodic patterns in a section of Time series. The first paper where they have focused on mining surprising periodic patterns in a sequence of events .In this paper, a more suitable measurement, information is introduced to naturally value the degree of surprise of each occurrence of a pattern as a continuous and monotonically decreasing function of its probability of occurrence. In this paper they have proposed a solution for new mining problem that is to find surprising periodic patterns in a sequence of data. This paper deals with the concept of how information and information gain are proposed to measure the degree of surprise of the pattern exhibited in a sequence of data. The other problem which has been dealt in this paper is downward closure. As download closure does not hold with information gain , they have devised an efficient algorithm to mine the surprising patterns and associated subsequence based on the bounded information gain property that is preserved by the information gain metric. In the previous papers of pattern discovery they made use of Apriori algorithm that can be stated as “if a pattern P is significant , then any sub pattern of P is also significant. The above mentioned paper proposes the solution to the said problem in the following manner. They introduced a new term called “Extensible Prefix” which they defined as A prefix is part of a pattern which can be generated by appending more events to the prefix .For an information gain threshold ,a prefix is extensible in a given sequence if at least one pattern with this prefix is surprising. We can follow from the above definition that all prefixes of a surprising pattern are extensible, and any pattern with an inextensible pattern cannot be a surprising pattern. And to prove the above they have used an algorithm called “BOUNDED INFORMATION GAIN” .The algorithm require the user to provide the expected the period value which is used to check the time series for the corresponding periodic pattern which is very difficult to provide expected period values. Another algorithm called “PARPER” which is one of the first work done in the field of mining partial periodic patterns. It forms the base of today?s works and it uses the basic mining algorithms such as apriori property and max-sub-pattern hit set property which makes it easy to understand. The paper deals with the mining periodic patterns partial in nature .All the studies before this paper have been based in full periodic patterns. In full periodic patterns, where every point in time contributes to periodicity but in partial periodicity the probability of repeating some time episodes is high. The paper assumes that a sequence of n time stamped data sets have been collected in database and they tried to find a pattern and sub-pattern. The paper in the discussion finds the patterns and their corresponding sub-patterns are found by giving the following input. |
| • A time series S. |
| • A specified period; or a range if periods specified by two integers high and low. |
| • An integer „n? indicating the ration of lengths of pattern „S? and the pattern must be least at a value „M?. |
| After giving the input they used “Single period apriori method” and “Single period max-subpattern hit set method” algorithms are used to get the required result. Parper fills the disadvantage of CONV algorithm which detects periodic patterns in a subsection time series but requires user to provide the expected period value. The next system based on this technique is an algorithm(detecting periodic patterns) which forms the base of my proposed system. All the previous work on the periodicity detection is done on the basis of user-specified time where the period is not known a prior. Those methods have higher degree of limitations and not feasible to implement as they are not cost effective and the performance |
| is O(n2) which is not good. So in this they proposed a method to reduce complexity and use both periodicity times and periodicity patterns for better results with the time complexity of O(nlogn) .In this paper, they addressed the problem of discovering potential periods in time series databases (periodicity detection). And defined two types of periodicities: segment periodicity and symbol periodicity. Whereas segment periodicity concerns the periodicity of the entire time series, symbol periodicity concerns the periodicities of the various symbols or values of the time series. For each periodicity type, a convolution-based algorithm is proposed and is analyzed, both theoretically and empirically. And they extended the symbol periodicity detection algorithm so that it can discover the periodic patterns of unknown periods, termed obscure periodic patterns. Hence, detected periodicity rates as well as frequent periodic patterns simultaneously. Although their algorithm works well with data sets having perfect periodicity, it fails to perform well when the time series contains insertion and deletion of noise. And it fails to detect patterns which are periodic in a subsection of the time series. |
PERIODICITY DETECTION – OUR APPROACH
|
| The proposed system is going to detect all 3 types of periodic patterns namely symbol, sequence, segment. The paper considers a time series T ( e0; e1; e2; . . . ; en-1) of length n, where „ei? denotes the event recorded at time i; and let T be discretized into symbols taken from an alphabet set „P? with enough symbols, i.e., „| P|? represents the total number of unique symbols used in the discretization process. In other words, in a systematic way T can be encoded as a string derived from P. For instance, the string „abbcabcdcbab? could represent one time series over the alphabet P ={a; b; c; d}. And this paper concentrates on the first case; Algorithm which is capable of detecting in an encoded time series (even in the presence of noise) symbol, sequence, and segment periodicity, which are formally defined next needs to be developed and hence the need to specify the degree of confidence in the reported result. |
Suffix-tree-based representation:
|
| The above mentioned problem can be solved by the use of an algorithm which uses “SUFFIX TREE” as underlying data structure which is a famous data structure that has been proven to be very useful in string processing . It can be efficiently used to find a substring in the original string, to find the frequent substring and other string matching problems. A suffix tree for a string represents all its suffixes; for each suffix of the string there is a distinguished path from the root to a corresponding leaf node in the suffix tree. Given that a time series is encoded as a string, the most important aspect of the suffix tree, related to our work, is its capability to very efficiently capture and highlight the repetitions of substrings within a string. Below figure shows a suffix tree for the string ssathishh$, where $ denotes end marker for the string; it is a unique symbol that does not appear anywhere in the string. The path from the root to any leaf represents a suffix for the string. Since a string of length n can have exactly n suffixes, the suffix tree for a string also contains exactly n leaves. Each edge is labeled by the string that it represents. Each leaf node holds a number that represents the starting position of the suffix yield when traversing from the root to that leaf. Each intermediate node holds a number which is the length of the substring read when traversing from the root to that intermediate node. Each intermediate edge reads a string (from the root to that edge), which is repeated at least twice in the original string. These intermediate edges form the basis of our algorithm presented later in this section. |
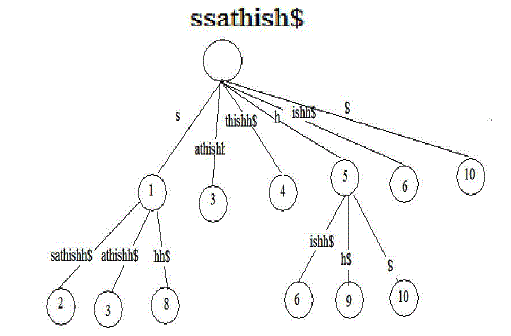 |
| Suffix tree for string ssathish$ |
| And we will use “Periodicity Detection Algorithm” and “Periodicity Detection in Presence of Noise” with the worst case complexity of O(k.n2), where „k? is the maximum length of the periodic pattern and „n? is the length of the analyzed portion(whole or subsection) of the time series. And the algorithm is noise resilient, which is able to work with replacement, insertion, deletion, or a mixture of these types of noise. We apply the periodicity detection algorithm at each intermediate edge using its occurrence vector. Our algorithm is linear distance-based, where we take the difference between any two successive occurrence vector elements leading to another vector called the difference vector. It is important to understand that we actually do not keep any such vector in the memory but this is considered only for the sake of explanation. (A,b,c,d,e) denoting the pattern, period value, starting position, ending position, and confidence, respectively. For each candidate period (p = diff vec[j]), the algorithm scans the occurrence vector starting from its corresponding value (c = occur vec[j]), and increases the frequency count of the period freq(p) if and only if the occurrence vector value is periodic with regard to c and p. This is presented formally in below Algorithm. |
DETECTION ALGORITHM
|
| For each occurrence vector „occur_vec? of size k for |
| pattern a, repeat |
| For j=0,j<n/2;j++ |
| B=occur_vec[j+1]-occur_vec[j]; |
| C=occur_vec[j]; |
| D=occur_vec[k]; |
| For i=j;i<k;i++; |
| If(c mod b== occur_vec[i] mod b) increment count(b); |
| End for |
| E(b)=count(b)/perfect_periodicity(b,c,a); |
| If(e(b)>=threshold) add b to period list; |
| End for |
| End for |
| End algorithm |
| The algorithm requires only a single scan of the data in order to construct the suffix tree; and the suffix tree is traversed only once to find all periodic patterns in the time series. An additional traversal of the suffix tree might be performed to sort the edges by the size of their occurrence vectors, but this is not among the necessary requirements of the algorithm. The algorithm basically processes the occurrence vectors of the intermediate edges. A suffix tree would have at most n intermediate edges because it contains at most 2n nodes and always n leaves. This means that we have to process at most n occurrence vectors. An occurrence vector may at most contain n elements (because we have n leaf nodes).Since we consider each element of the occurrence vector as candidate starting position of the period and each difference value is candidate period, the complexity of processing an occurrence vector of length n would be O(n2). Since there can be at most n occurrence vectors, the worst-case complexity of the algorithm comes out as O(n3), which is not a very good theoretical result. But fortunately, this is not the case in general, i.e., the proposed algorithm depicts the O(n3) complexity in very rare cases. One interesting observation about periodic patterns is that generally they are not too long. The length of periodic patterns is independent of the size of the time series. To analyze the average-case complexity of the proposed algorithm, it is worth noting that the average depth of the suffix tree has been reported to be of order log(n) .Accordingly, the averagecase complexity of the proposed algorithm would be O(n2logn). |
CONCLUSION
|
| In this paper, we have presented STNR as a suffix-tree-based algorithm for periodicity detection in time series data. Our algorithm is noise-resilient and run in O(k.n2) in the worst case. The single algorithm can find symbol, sequence (partial periodic), and segment (full cycle) periodicity in the time series. This algorithm runs on both real and synthetic data. |
References
|
- InfoMiner: Mining Surprising Periodic Patterns by Jiong Yang, Wei Wang, Philip S. Yu
- Periodicity Detection in Time Series Databases by Mohamed G. Elfeky, Walid G. Aref, Senior Member, IEEE, and Ahmed K. Elmagarmid,IEEE
- Efficient Mining of Partial Periodic Patterns in Time Series Database by Jiawei Han, Guozhu Dong
- R. Grossi and G.F. Italiano, “Suffix Trees and Their Applications in String Algorithms,” Proc. South Am. Workshop String Processing, pp. 57-76
- F. Rasheed and R. Alhajj, “STNR: A Suffix Tree Based Noise Resilient Algorithm for Periodicity Detection in Time Series Databases,”Applied Intelligence, vol. 32, no. 3, pp. 267-278, 2010.
- F. Rasheed and R. Alhajj, “Using Suffix Trees for Periodicity Detection in Time Series Databases,” Proc. IEEE Int?l Conf. Intelligent Systems, Sept. 2008.
- E. Ukkonen, “Online Construction of Suffix Trees,” Algorithmica, vol. 14, no. 3, pp. 249-260, 1995.
- K.-Y. Huang and C.-H. Chang, “SMCA: A General Model for Mining Asynchronous Periodic Patterns in Temporal Databases,”IEEE Trans. Knowledge and Data Eng., vol. 17, no. 6, pp. 774-785, June 2005.
- S. Ma and J. Hellerstein, “Mining Partially Periodic Event Patterns with Unknown Periods,” Proc. 17th IEEE Int?l Conf. Data Eng., Apr. 2001.
|