Modeling Pressure Dependent Elastic Parameters of GaAsSb Alloy

Abstract

Density functional theory with GGA approximation elastic properties of GaAs1-xSbx of x=0.5 have been calculated from 0-20 GPa range of pressure. The geometry adjusted structural parameters for GaAs1-xSbx under separate pressures and they are listed. It was detected that lattice constant decreased by pressure increasing. Furthermore, parameter B decreased and parameter S and Y increased by pressure increasing. The elastic constants fulfilled the customary mechanical stability conditions for the ternary intermingled crystals. The elastic modulus was gained. The adjusted elastic constants varied with various rates under increasing pressure.

Keywords

Alloy, Elastic parameters, Pressure

Introduction

Semiconductor alloys have been concentrated on so much due to their capability to adapt the optoelectronic properties with growth of semiconductor technologies like the band gap with the alloy compositions. The III-V compounds and their solid solutions were operative in the semiconductor devices working. The GaAs1–xSbx alloys were absorbing materials for optoelectronic applications due to the wide band gap range from 0.87 to 1.65 μm, varying with the Sb content [1]. Nevertheless, all wavelengths could not be gained due to the presence of a miscibility gap in the composition range 0.39<x<0.62. The devices in the existent study were negative electron affinity photocathodes, photodiodes, light emitting diodes, double heterostructure lasers, and room temperature cw lasers [2]. The GaAs1–xSbx ternary alloys, particularly, were actually beneficial for high efficiency cascade solar cells. The As-Ga-Sb system displayed a eutectic valley ranging from the Sb rich side of the binary Ga-Sb phase diagram to the As rich region of the As-Ga phase diagram. Owing to the high vapor pressure of As, the phase diagram determinations have been restricted to As dilute compositions. The quasi binary section GaAs-GaSb in the ternary phase diagram was a region of extended solid solution with a larger region of immiscibility in the solid phase [3-5].

The high-pressure structural stability of the III-V binary alloys has been the focus on by tremendous research for more than twenty years but the high-pressure phase diagrams of the GaAsSb alloys have not been completely indicated. This was moderately owing to the definite sample-handling difficulties that arise in coping with these alloys. Empirically, all these alloys adopt the zinc-blende structure at low and moderate pressures. Before the current study, we have conducted a study on GaAs0.5Sb0.5 structure and optical properties using density functional theory [6]. On the other hand, we have carried out a study on mechanical properties of the Lead Sulfur Selenium under separate pressure [7]. Furthermore, many other theoretical and experimental studies have been done about structure, elastic and optical properties of GaAs1-xSbx alloys [8-10].

The study was significant because it was conducted for the first time in terms of studying elastic properties of GaAs0.5Sb0.5 alloy under pressure. This study was carried out to shed light on the future studies which will practically be conducted and test these alloys in laboratories, to help them in determining the change in amounts of additives in alloys, and to determine the accordance of theoretical and experimental studies with other theoretical works. The elastic properties of GaAs0.5Sb0.5 will vary under different pressure, which directly impacts separate applications of GaAs-based devices under methods of other works. Taking into account of different application conditions, the elastic properties of Gallium arsenic antimony of x=0.5 at 0-20 GPa are studied using density functional theory in the current work.

Modeling Method

The Elastic properties of GaAs1−xSbx ternary alloys are investigated using the CASTEP program [10]. Which is founded on density functional theory using a plane-wave basis set for the extension of the wave functions [11-13]. Generalized gradient approximation (GGA) is made for electronic exchange-correlation potential energy. Coulomb potential energy caused by electron-ion interaction is described using pseudo-potential concept [14]. Monkhorse-pack mesh was used to determine 56 k-points for bulk calculation. A plane-wave cutoff energy of 360 eV was utilized. It was displayed that the outcomes were well converged at this cutoff. The Ga (3d¹⁰4s²p¹), As (3d¹⁰4s²4p³) and Sb (4d¹⁰5s²5p³) were treated as valence state. Geometry optimization is performed for GaAs_1−xSb_x of x=0.5 with symmetry P1. Atomic position optimized with a density mixing scheme [15] using the conjugate-gradient (CG) method [16] for eigenvalues minimization. The following thresholds for converged structures were operated: energy change per atom <2 x 10⁶ eV, residual force 0.5 eV/nm, stress below 0.05 GPa, and the dis-placement of atoms during the geometry optimization 0.001 nm. In mechanical properties, the element is acted by external forces in state and stress. Additionally if the body is in equilibrium, the external stress must be exactly balanced by internal forces [17,18]. In an atomistic calculation, the internal stress tensor can be achieved using the so-called virile expression

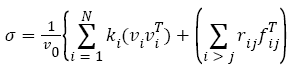(1)

Where index i runs over all particles 1 through N, k_i, v_i and f_i denote the mass, velocity and force acting on particle i, and V₀ denotes the (undeformed) system volume.

For a parallelepiped (e.g., a periodic simulation cell) regarded as in some reference states by the three column vectors a0, b0, c0, and by the vectors a, b, c in the deformed state, the strain tensor is displayed by:

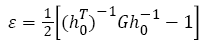(2)

Where h0 denotes the matrix formed from the three column vectors a₀, b₀, c₀, h denotes the corresponding matrix formed from a, b, c, T denotes the matrix transpose, and G denotes the metric tensor hTh The elastic stiffness coefficients, relating the various components of stress and strain are defined by:

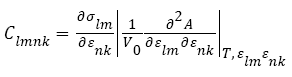(3)

Where A denotes the Helmholtz free energy. For small deformations, the relationship between the stresses and strains may be expressed in terms of a gen- eralized Hooke’s law:

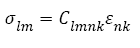(4)

(5)

Where S_lmnk denote the compliance components. Note that in both Equations (4) and (5), the summation convention is implied. For example, s₂₁ is given in full as:

The generalized Hooke’s law is thus often written as:

(6)

Try to note that the 6 x 6 stiffness matrix C is also symmetric, and hereafter a maximum of 21 coefficients is essential to entirely explain the stress-strain behavior of an arbitrary material.

Moreover, note that C is no longer a tensor, since it does not abide by the required transformation rules. For an isotropic material, the stress-strain behavior can be entirely defined by identifying only two independent coefficients.

(7)

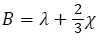(8)

Where λ and χ are regarded as the Lame coefficients.

For the isotropic case, expressions used for the Young modulus Y, bulk modulus B, and Shear modulus S are shown as follows [19,20].

The elastic parameters were premeditated by the limited strain method in which the ground state structure was strained in line with symmetry-dependent strain patterns with changing capacities and a posterior analysis of the stress tensor after are optimization of the internal structure parameters. Additionally, the bulk modulus B, shear modulus S and the young modulus were calculated from the elastic parameters.

Result and Discussion

The elastic properties were explored to realize the response of GaAs_0.5Sb_0.5 under ambient and high pressure. Structural properties comprising structure stability through optimizations, lattice constant a₀, band gap energy (Eg) and minimum volume (V₀) and ground state energy (E₀) have been found and compared with the obtainable data in the current study. For elastic properties comprising ductile or brittle nature of the alloy, elastic constants (c_ij), bulk modulus (B), young modulus(Y), and the shear modulus have been discoursed. The mentioned properties above were found using density functional theory.

The lattice constants of alloys at equilibrium have been calculated in the first phase by minimizing the lattice parameter of the crystal and the ratio of total energy of the crystal to its volume. The geometry structural parameters were optimized for GaAs0.5Sb0.5 alloys under separate pressures as displayed in Table 1.

Table 1. Structural properties of GaAs_0.5Sb_0.5.

It can be seen that lattice constant a₀ has been decreased and energy band gap E_g has been increased with pressure increasing. On the other hand, ground state energy E₀ has been decreased with pressure increasing. To further knowledge, many materials regularly become metallic with pressure increasing. Additionally, as the atoms get closer, lattice parameter decreases, thus, all modulus enlarge. In the GaAs_0.5Sb_0.5 alloys, lattice parameter also decreases. The atoms come closer to each other and hence modulus enlarges, and these materials become metallic with pressure increasing.

We optimized minimum volume (V₀) and the ground state energy (E₀) of unit cell through volume as displayed in Figure 1, i.e. pressure=20 GPa to save space in this article. In the volume optimization procedure, ground state energy and minimum volume display the alloy stability with various pressures. We result from our optimizations that GaAsSb stay in stable cubic phase even at such extreme pressure conditions. This displays the capability of alloy to maintain pressure without phase transforming.

Figure 1: Optimization structure of GaAs_0.5 Sb_0.5.

As seen in Figure 2, elastic modulus of GaAs_0.5Sb_0.5 alloys under separate pressures was shown. Particularly, they give information on the stability and rigidity of materials, and their ab initio calculation needs definite methods. Since the forces and the elastic constants are functions of the first-order and second-order derivatives of the potentials, their calculation will give a deeper check on the exactness of the calculation of forces in solids. The second-order elastic constants (C_ij) are calculated using the “volume-conserving” method [20] and the findings are explained in Table 2.

Figure 2: Pressure dependence of the elastic parameters c_ij.

Table 2. Calculated elastic Properties of GaAs_0.5Sb_0.5 under different pressure.

For a stable tetragonal structure, the six independent elastic constants C_ij (C₁₁, C₁₂, C₁₃, C₃₃, C₄₄ and C₆₆) ought to satisfy the notable Born-Huang criteria for stability [21-23],

C₁₁>0, C₃₃>0, C₄₄>0, C₆₆>0, (C₁₁-C₁₂)>0, (C₁₁+C₃₃-2C₁₃)>0,

{2 (C₁₁+C₁₂)+C₃₃+4C₁₃}>0.

The cubic crystals embrace the three dependent elastic constants C_ij (C₁₁, C₁₂, C₁₄) which explain inequalities, (C₁₁- C₁₂)>0, C₁₁>0, C₄₄>0, (C₁₁+2C₁₂)>0. Our outcomes for elastic constants in Table 2 abide by these stability conditions for GaAs_0.5Sb_0.5 alloys.

Table 3. Comparison and Difference between Elastic Constants of the Present Study (PS) and Other Studies (OS).

The elastic constants C_ij are very prominent for some mechanical properties of GaAs_0.5Sb_0.5 particularly in some specific application conditions including internal strain and thermo-elastic stress. The calculated results of C_ij of GaAs_0.5Sb_0.5 as a function of pressure from 0 to 20 GPa are displayed in Table 2. For these alloys, no empirical and theoretical data exist. As can be seen, we find that C₁₁, C₁₂ and C₄₄ increase with pressure increasing. On the other hand, C₁₃, C₃₃ and C₆₆ decrease with diverse rates under pressure increasing. The achieved elastic parameters, namely C₁₁, C₁₂, C₁₃, C₃₃, C₄₄, and C₆₆, for the material under separate pressure which have been studied at various compositions x=0.5 are displayed in Table 2. Theoretical data has been compared at pressure equal to 0 GPa only, because no experimental and theoretical data exist under different pressures. Furthermore, there is an agreement between the results of C₁₁ and C₁₂. Theoretically, the obtained result is 3% higher than the result [24].

Figure 2 shows elastic modulus of GaAs_0.5Sb_0.5 alloys under separate pressures, S is the shear modulus, and Y is the Young modulus. Parameter Y decreases with pressure increasing (Figure 3). Also, S increases, as pressure increases (Figure 4). In the current case, the bulk modulus B of GaAs_0.5Sb_0.5 alloys was investigated under separate pressures (P=0, 10 and 20 GPa). Compressibility in accordance with the value decreasing of separate pressure can be seen in Figure 5. The elastic constants of solids deliver a relation between the mechanical and dynamical behavior of crystals, and provide significant information regarding the nature of the forces operating in solids.

Figure 3: Pressure dependence of the young modulus.

Figure 4: Pressure dependence of the shear modulus.

Figure 5: Pressure dependence of the Bulk modulus.

The current result concerning bulk modulus is supported by the theoretical and experimental data [22-25]. They are all presented in Table 3.

The elastic parameters of the GaAs_0.5Sb_0.5 alloys have been profoundly assessed. To the best of our knowledge, there are only few reports up-to-date for the alloys under separate pressures. Comparison between our numerically calculated results concerning elastic parameters and those obtained from the other works are listed in Table 3. The values noted in this table in terms of the elastic constants consider that the variances between the data calculated in the current work and those assessed from the other works are less than 5% for C₁₁ and 9% for C₄₄, whereas for the bulk modulus and shear modulus the variance is larger than 4%. In view of that, one might result that the parameters derived from the other works are not commonly diverse from the calculated ones which does not display approximately a deviation of material studied properties from linearity in line with Sb composition x=0.5.

Conclusion

In the current work, the elastic properties of Gallium Arsenic Antimony of x=0.5 are investigated using density functional theory. The results are achieved by a first-principles technique based on the GGA using plane-wave pseudo potentials. The geometry optimized structural parameters for GaAs_0.5Sb_0.5 under separate pressures are indicated. The elastic parameters satisfy the traditional mechanical stability conditions for these ternary intermingled crystals. The lattice parameters decrease as pressure increases. Besides that, parameter S and Y increase as pressure increases but parameter B decreases with adding pressure. The calculated results of C_ij of GaAs_0.5Sb_0.5 as a function of pressure from 0 to 20 GPa are indicated. C₁₁, C₁₂ and C₄₄ parameters increase with separate rates under pressure increasing. On the other hand, C₁₃, C₄₄ and C₆₆ parameters decrease under pressure increasing.

Acknowledgements

The author would like to thank Dr. Srwa Saeed and Mr. Murad Sh. Othman for some helpful suggestions and discussions.

References

1. Scholz RF and Gösele U. Phosphorus and antimony in GaAs as tracers for self-diffusion on the arsenic sublattice. J Appl Phys 2000;87:704-710.
2. Cherng MJ, et al. OMVPE growth of the metastable III/V alloy GaAs0. 5Sb0. 5. J Electronic Mater 1986;15:79-85.
3. Vurgaftman, I, et al. Band parameters for III–V compound semiconductors and their alloys. J Appl phys 2001;89:5815-5875.
4. Klenovský, et al. Electronic structure of InAs quantum dots with GaAsSb strain reducing layer: localization of holes and its effect on the optical properties. Appl Phys Lett 2010;97:203107.
5. Ashrafi MJ, et al. A 3-D constitutive model for pressure-dependent phase transformation of porous shape memory alloys. J Mech Behav Biomed Mater 2015; 42:292-310.
6. Othman, et al. Structural and Optical Properties of GaAs0.5Sb0.5 and In0.5Ga0.5As0.5Sb0.5: Ab initio Calculations for Pure and Doped Materials. Chinese Phys Lett 2012;29:037302.
7. Othman MS. Simulation mechanical properties of lead sulfur selenium under pressure. J Mod Phys 2015;4:185.
8. Gorman BP, et al. Atomic ordering-induced band gap reductions in GaAsSb epilayers grown by molecular beam epitaxy. J Appl Phys 2005;97:063701.
9. Teissier R, et al. Temperature-dependent valence band offset and band-gap energies of pseudomorphic GaAsSb on GaAs. J Appl Phys 2001;89:5473-5477.
10. Othman, et al. Ab-initio investigation of structural, electronic and optical properties of InxGa1−xAs, GaAs1−yPy ternary and InxGa1−xAs1−yP y quaternary semiconductor alloys. J Alloy Compd 2010;496:226-233.
11. Hohenberg P and Kohn W. Inhomogeneous electron gas. Phys Rev 1964;136:B864.
12. Othman, et al. The structural, electronic and optical properties of InxGa1−xP alloys. Physica B: Condsd Mat 2010;405:2357-2361.
13. Holzwarth, et al. A Projector Augmented Wave (PAW) code for electronic structure calculations, Part I: atompaw for generating atom-centered functions. Comp Phys Commun 2001;135:329-347.
14. Othman, et al. Ab-initio investigation of electronic and optical properties of InAs1-xPx alloys. Gazi Univ J Sci 2010;23:149-153.
15. Monkhorst HJ and Pack JD. Special points for Brillouin-zone integrations. Phys Rev B 1976;13:5188.
16. Oloumi M and Matthai CC. Electronic structure and band discontinuities in the InAs/GaAs system. J Phys: Condensed Matt 1990;2:5153.
17. Segall, et al. First-principles simulation: ideas, illustrations and the CASTEP code. J Phys: Condensed Matt 2002;14:2717.
18. Pople,et al. Kohn-Sham density-functional theory within a finite basis set. Chem Phys let 1992;199:557-560.
19. Wei L, et al. Electronic and elastic properties of PbS under pressure. Physica B: Condnsd Matt 2010;405:1279-1282.
20. Liou BT, et al. First-principles calculation for bowing parameter of wurtzite InxGa1−xN. Opt Commun 2005;249:217-223.
21. Agrawal BK and Agrawal S. Ab initio calculation of the electronic, structural, and dynamical properties of AlAs and CdTe. Phys Rev B1992;45:8321.
22. Bouarissa N. Elastic constants and acoustical phonon properties of GaAsx Sb1−x. Mat Chem Phys 2006;100:41-47.
23. Dheeraj DL. Growth and characterization of wurtzite GaAs nanowires with defect-free zinc blende GaAsSb inserts. Nano lett 2008;8:4459-4463.
24. Wang SQ and Ye HQ. First‐principles study on elastic properties and phase stability of III–V compounds. Phys status solidi B 2003;240:45-54.
25. Detz H and Strasser G. Modeling the elastic properties of the ternary III–V alloys InGaAs, InAlAs and GaAsSb using Tersoff potentials for binary compounds. Semicond Sci Technol 2013;28:085011.