Keywords
|
| Dijkstra’s algorithm, Time Complexity, Road Network |
INTRODUCTION
|
| The current widespread use of location-based services and GPS technologies has revived interest to develop a very fast and scalable shortest path algorithm to find a valid route for travelers over the road networks. Computing shortest path or distance between two points is one of the most fundamental and important key problems on road networks. Many people frequently faces lot of problem while planning their trips with their own vehicles. Recent days many applications were developed to solve problem by finding an efficient route for the road networks. The past literature shows that various shortest path algorithm were developed to find the valid route for the road networks. But still the problem resists. Hence, the objective of the research is to propose a new shortest path algorithm to provide a better solution for the travelers over the road networks. |
| Due to the development of geographic information systems (GIS) technology it is possible to determine the fastest route and dispatch an emergency vehicle like ambulance, fire service vehicle etc. with the assistance of GIS. Because a link on a real road network in a city tends to possess different levels of congestion during different time periods of a day, and it is not an easy task to locate a shortest path [1]. Hence, the fastest route can only be determined in real time. In some cases the fastest route has to be determined in a few seconds. Moreover, when large road networks are involved in an application, the determination of shortest paths on a large network can be computationally very difficult because many applications are involved to find the shortest path over the road networks. |
| During the 1980s and 1990s, a lot of work has been done on improving the existing algorithms, these works are mainly focused on searching the shortest path from one origin to one destination in large scale road maps [2]. The introduction of the navigation systems has leads to many new techniques. Most of the research concentrated on preprocessing the network first. During the preprocessing, some additional information is determined. This information can be used in any SPP-algorithm to reduce the computational complexity and to provide the better results. |
RELATED WORK
|
Graph Theory
|
| A graph is mathematical concept formally defined by a set of vertices (or nodes) V and a set of edges E connecting these vertices. Edges are called directed if for a pair of vertices, an edge can be used to travel from one node to the other but not the other way around. Edges may also have a numerical value, often called the weight or cost, which are an abstract representation of the “work” needed to move along that edge. Only these basic concepts are needed to understand the shortest path problem; for the more advanced concepts, please refer to [3]. Graphs are often used as abstract representations of networks, e.g. a road-map, map of linguistic distance between words etc. and can discretize an environment into “checkpoints” to enable navigation by artificial intelligence agents. |
Overview of Shortest Path Algorithm
|
| Over the past decades there are various shortest path algorithm were developed. The shortest path algorithm are classified into three categories they are Single source shortest path algorithms, Single destination shortest path algorithms, All-Pairs shortest path algorithms and it is shown in below figure 1. |
Djikstra’s Shortest Path Algorithm
|
| It is a general case of the breadth-first search algorithm and can be seen as the ancestor of many modern path finding techniques [4]. Beginning at the source vertex, we assign each adjacent vertex the cost value of the edge joining them. Next, we process the vertex with the least accumulated cost and assign the accumulated cost plus the edge cost to each of its adjacent vertices. This step is repeated until each vertex has been processed. If a vertex is revisited, we assign it the new cost if it is lower than the currently assigned cost. At the end of the algorithm, we have solved not only the single pair shortest path problem, but can find the distance between the source vertex and any other vertex. |
| The Dijkstra’s shortest path algorithm is the most commonly used to solve the single source shortest path problem today. For a graph G (V, E), where V is the set of vertices and E is the set of edges, the running time for finding a path between two vertices varies when different data structure are used. This project uses binary heap to implement Dijkstra’s algorithm although there are some data structures that may slightly improve the time complexity, such as Fibonacci heap that can purchase time complexity of O(V*log(V)). |
Time Complexity
|
| The run time of first for loop is O(V). In each iteration of the while loop, Extract_Min of the heap is logV. The inner for loop iterates each adjacent node of the current node, the total run time is O(E). Therefore, the time complexity of this algorithm is O((V + E)*log(V) = O(E* log(V)). The correctness of this algorithm is well proved in [5]. As the number of nodes in a graph increases, the running time of the applied algorithm will become longer and longer. Usually, a road network of a city has more than 10^4 nodes. A fast shortest path algorithm becomes more desirable Mohring et al. analyzed the existing different Dijkstra’s shortest path algorithm. They found that in the existing Dijkstra’s algorithm. |
Literature Review
|
| Bauer et al. identified that there was a need to find an efficient shortest path route for the road network. Hence, they developed a new shortest path algorithm by modifying the Dijkstra’s shortest path algorithm using Combining hierarchical and goal-directed technique. This algorithm shows the better results than the existing Dijkstra’s shortest path algorithm but it take high computational time than the existing algorithm. |
Dijkstra’s shortest path algorithm
|
| for each u ∈ G; |
| d[u] = infinity; |
| parent[u] = NIL; |
| End for |
| d[s] = 0; // s is the start point |
| H = {s}; // the heap |
| while NotEmpty(H) and targetNotFound: |
| u = Extract_Min(H); |
| label u as examined; |
| for each v adjacent to u: |
| if d[v] > d[u] + w[u, v]: |
| d[v] = d[u] + w[u, v]; |
| parent[v] = u; |
| DecreaseKey[v, H]; |
| Goldberg et al. analyzed the various shortest path algorithms. They found that there is lot of problems present in the existing algorithms. Hence they developed a shortest path algorithm called A* shortest path algorithm. This algorithm is the extension of Dijkstra’s. In this they include the new parameters like cost, modified weighs etc. This algorithm provides the better result compared to the existing Dijkstra’s shortest path algorithm [6, 7]. |
| The computational complexity is very high. Hence they decided to reduce the computational time of the existing algorithm. So they developed a shortest path algorithm using a Partitioning Graphs technique in the Dijkstra’s algorithm to reduce the computation [8, 9, 10]. |
PROPOSED ALGORITHM
|
| Computing shortest path or distance between two points is one of the most fundamental and important key problems on road networks. Many people frequently face lot of problem while planning their trips with their own vehicles. Recent days many applications were developed to solve problem by finding an efficient route for the road networks. The past literature shows that various shortest path algorithm were developed to find the valid route for the road networks. But still the problem resists. Hence, there is a need to propose a new shortest path algorithm to provide a better solution for the travellers over the road networks. |
| Due to the development of geographic information systems (GIS) technology it is possible to determine the fastest route and dispatch an emergency vehicle like ambulance, fire service vehicle etc. with the assistance of GIS. Because a link on a real road network in a city tends to possess different levels of congestion during different time periods of a day, and it is not an easy task to locate a shortest path. Hence, the fastest route can only be determined in real time. In some cases the fastest route has to be determined in a few seconds. Moreover, when large road networks are involved in an application, the determination of shortest paths on a large network can be computationally very difficult because many applications are involved to find the shortest path over the road networks. |
| In the past literature, numerous shortest path algorithms like Dijkstra’s algorithm, Bellman-Ford algorithm, A* search algorithm, Floyd Warshall algorithm and Johnson’s algorithm were developed. A thorough analysis was performed on the existing shortest path algorithms. Finally, it was observed that Dijkstra's shortest path algorithm is the most appropriate for calculating shortest path in road networks. But the existing Dijkstra's shortest path algorithm needs some modification to improve the efficiency and to find a valid shortest path and to reduce the computational complexity. Hence, a new algorithm called Modified Dijkstra’s Shortest Path algorithm (MDSP) is proposed |
Modified Dijkstra’s Shortest Path Algorithm (MDSP)
|
| A new shortest path algorithm called Modified Dijkstra’s Shortest Path algorithm (MDSP) is proposed. In this algorithm multiple parameters were used to find the valid shortest path instead of using single parameter. The efficiency of the MDSP algorithm is analysed in terms of shortest path by measuring its nodes and Time complexity. |
Algorithm 1: MDSP
|
| begin |
| for each vertex v in Graph do |
| alternate_path[i]:=NULL; |
| dist[v] := infinity; |
| weight_update(choice); |
| for each vertex v in Graph do |
| if v= source or v |
| = destination then |
| for each neighbour u of v do |
| if alternate_path[i] > dist[u] + |
| distance(u,v) then |
| alternate_path[i]:= dist[u] + |
| distance(u,v); |
| end if |
| end for |
| end if |
| end for |
| end for |
| end |
Algorithm 2: Including Multiple Parameter
|
| begin |
| if c = d then; |
| else if c = t then |
| d := d * s; |
| Else |
| d:= d* z; |
| return d; |
| endwhere |
| c = choice |
| d= distance |
| t=time |
| s=time factor |
| z=congestion factor |
RESULT ANALYSIS
|
| The efficiency of the MDSP algorithm is verified in terms nodes (it shows the shortest path) and Time using Jaipur city database. For this experiment a tool was developed using Java. In this tool existing and proposed algorithm were implemented. To perform experiment analysis, we considered the Jaipur database. The proposed algorithm is compared with the existing modified Dijkstra’s algorithms namely, Dijkstra’s Algorithm with Buckets (DKB), Dijkstra’s Algorithm with Double Buckets (DKD), Dijkstra’s algorithm with Approximate Buckets (DKA). |
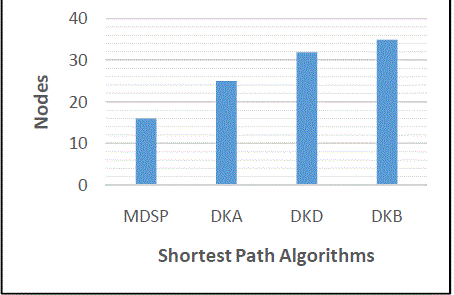
| To prove that the proposed MDSP algorithm efficiently select the shortest is achieved by computing the nodes taken to select the efficient shortest path. The nodes for the three different algorithms and our proposed algorithm were computed and their results are displayed in the Table 1. Figure 3 shows the comparative analysis of the existing algorithm and the proposed algorithm MDSP. The comparative analysis shows that MDSP takes minimum number of nodes than the other three existing algorithms. |
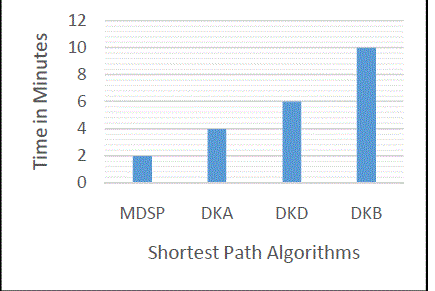
| The proposed MDSP algorithm reduces the time complexity. This is achieved by computing the time taken to find the efficient shortest path. Table 2 shows the result of the time taken for the existing shortest path algorithms and the proposed MDSP algorithm. A comparative analysis is performed with the existing three shortest path algorithms with the MDSP and the results are displayed in the figure 4. The comparative analysis shows that MDSP take lesser time to compute the efficient shortest path than the existing algorithms. |
| From the table 1 and 2 the result of the experiment analysis shows that the proposed shortest path algorithm MDSP finds the valid shortest path because compared to the existing algorithm it take only minimum number of nodes and also it takes less computation time. Hence the proposed MDSP algorithms perform better than the existing three modified Dijkstra’s shortest path algorithms. |
CONCLUSION
|
| Many research works are carried out to solve the shortest path problem for road networks. In this paper, a new shortest path algorithm namely MDSP was proposed with the multiple features. The algorithm is developed by considering the various problems present in the existing modified Dijkstra’s shortest path algorithms. In this MDSP algorithm, instead of single parameter multiple parameters were included to find the valid shortest path for road networks. The results of the MDSP algorithms prove that, that the proposed algorithm efficiently finds the shortest path for road network with minimum time complexity. |
Tables at a glance
|
 |
 |
| Table 1 |
Table 2 |
|
| |
Figures at a glance
|
 |
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
Figure 4 |
|
| |
References
|
- Brunel, E., Delling, D., Gemsa, A., and Wagner, D., “Space-efficient SHARC-routing”, 9th International Symposium on Experimental Algorithms (SEA). 2012, 47-5858.
- Bauer, R. and Delling, D. 2009., “SHARC: Fast and robust unidirectional routing”, ACM Journal of Experimental Algorithmics 14. Announced at ALENEX 2008.
- Bauer, R., Delling, D., Sanders, P., Schieferdecker, D., Schultes, D., and Wagner, D. ,”Combining hierarchical and goal-directed speed-up techniques for Dijkstra's algorithm”, ACM Journal of Experimental Algorithmics, 2010, pp 34-42.
- Thomas H. Cormen, Charles E.Lieserson, Ronald L. Rivest, Clifford Stein, “Introduction to Algorithms”, Prentice Hall of India, 2009.
- AnanyLevitin, “Introduction to the design & analysis of algorithms”, Pearson Education, Second Edition, 2009.
- D. Delling, A. V. Goldberg, T. Pajor, and R. F. Werneck. Customizable route planning. In SEA, pages 376-387, 2011.
- D. Delling, A. V. Goldberg, and R. F. Werneck, ” Hub label compression”, SEA, pages 18-29, 2013.
- M. Hilger, E. Kohler, R. H. Mohring, and H. Schilling, “Fast point-to-point shortest path computations with arc- ags. The Shortest Path Problem”, Ninth DIMACS Implementation Challenge, 74:41-72, 2009.
- Abraham, D. Delling, A. V. Goldberg, and R. F. Werneck, “A hub-based labeling algorithm for shortest paths in road networks”, SEA, pages 230-241, 2011.
- Abraham, D. Delling, A. V. Goldberg, and R. F. Werneck, “Hierarchical hub labelings for shortest paths”, ESA, pages 24-35, 2012.
|