Research & Reviews: Journal of Material Sciences
MenuISSN:2321-6212
ISSN:2321-6212
College of Information Engineering, China Jiliang University, Hangzhou 310018, China
Received Date: 11/09/2017; Accepted Date: 25/09/2017; Published Date: 05/10/2017
DOI: 10.4172/2321-6212.1000194
Visit for more related articles at Research & Reviews: Journal of Material Sciences
Super elliptical plates which are defined by shapes between an ellipse and a rectangle have a wide range of use in engineering applications. Investigations on non-linear behaviors of super elliptical isotropic plates are available in the literature, while investigations on nonlinear behaviors of FGM super elliptical plates haven’t been reported at present. In this paper, nonlinear bending and thermal post-buckling analysis are first presented for functionally graded super elliptical plates based on classical plate theory. Material properties are assumed to be temperature-dependent and graded in the thickness direction. The numerical illustrations concern the nonlinear behaviors of functional graded plates with immovable simply supported edge and immovable clamped edge. Influences played by different supported boundaries, thermal environmental conditions, and volume fraction index are discussed in detail using Ritz method.
Rectangular plates with rounded corners are used extensively in industrial applications as structural and machine elements. Although rounded corners are advantageous in helping to diffuse and dilute stress concentrations. Super elliptical plates which are defined by shapes between an ellipse and a rectangle have a wide range of use in engineering applications. Some studies [1-16] for linear behaviors of super elliptical plates are available in the literature. Wang et al. [1] presented accurate frequency and buckling factors for super elliptical plates with either simply supported or clamped edges by using Rayleigh-Ritz method. Lim et al. [2] investigated free vibration of doubly connected super-elliptical laminated composite plates. Then Chen et al. [3] reported a free vibration analysis of laminated thick super elliptical plates. Liew and Feng [4] studied threedimensional free vibration analysis of perforated super elliptical plates. Zhou et al. [5] analysed three-dimensional free vibration of super elliptical plates based on linear elasticity theory using Chebyshev-Ritz method. Altekin [6] gave out free linear vibration and buckling of super-elliptical plates resting on symmetrically distributed point-supports, Altekin and Altay [7] calculated static analysis of point-supported super-elliptical plates, then Altekin [8,9] discussed free vibration and bending of orthotropic super elliptical plates on intermediate supports. Çeribaşı et al. [10] gave out static linear analysis of super elliptical clamped plates based on the classical plate theory by Galerkin’s method, Çeribaşı and Altay [11] investigated free vibration of super elliptical plates with constant and variable thickness by Ritz method, then Çeribaşı [12] investigated static and dynamic linear analyses of thin uniformly loaded super elliptical clamped functionally graded plates. Jazi and Farhatnia [13] discussed buckling of functionally graded super elliptical plate based on the classical plate theory using Pb-2 Ritz method. Hasheminejad et al. [14] investigated the dynamic instability of thin, clamped, flat isotropic elastic panels of super elliptical planform set on a two-parameter Winkler-Pasternak foundation and subjected to uniformly distributed pulsating in-plane loads. Ghaheri et al. [15] investigated static and parametric stability of thin symmetrically laminated composite super-elliptical plates resting on Winkler-type foundation and subjected to uniform in-plane harmonic loads, under clamped, simply supported and free boundary conditions. Altunsaray [16] presents static bending analyses of symmetrically laminated quasi-isotropic super-elliptical thin plates, and calculations were performed by using the Rayleigh-Ritz method based on the classical laminated plate theory.
Investigations on non-linear behaviors of super elliptical plates are limited in the literature. Zhang [17] first reported investigations on non-linear bending of super elliptical plates. Then, Zhang and Zhou [18] presented non-linear symmetric free vibration analyses of super elliptical isotropic thin plates with simply supported edge and clamped edge based on classical plate theory.
Functionally graded materials (FGMs) are typically characterized by a smooth and continuous change of the mechanical properties from ceramics surface to metal surface, and can be used in many engineering applications, especially in high temperature environments such as aerospace structures, fusion reactors and nuclear industry due to their better thermal resistance characteristics. And FGM super elliptical thin plates are potential in future engineering application. As far as known to the author, investigations on nonlinear behaviors of FGM super elliptical plates haven’t been reported. In this paper, the present work focuses attention on nonlinear bending and thermal post-buckling analysis of functionally graded super elliptical plates based on classical plate theory. The material properties of functionally graded materials are assumed to be temperaturedependent, and graded in thickness direction according to a volume fraction power law distribution. Approximate solutions of FGM super elliptical plates are obtained by Ritz method.
Functionally graded materials are usually made from a mixture of metals and ceramics, their material properties exhibit a smooth and continuous change from one surface to another by gradually varying the volume fraction of constituent materials, thus eliminating interface problems and mitigating thermal stress concentrations, so FGMs are now developed for general use as structural components in extremely high temperature environments.
Consider a FGM super elliptical plate of major axis 2a, minor axis 2b and thickness h, and the coordinate system is illustrated in Figure 1.
Figure 1: Geometry and coordinates of a FGM super elliptical plate.
The boundary shape equation of the super elliptical plates can be represented by:
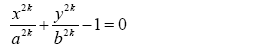
k is the power of the super ellipse, and if k=1, the shape becomes an ellipse, if k=∞, the shape becomes a rectangle. According to classical plate theory, it can be assumed that the displacement fields are:
k is the power of the super ellipse, and if k=1, the shape becomes an ellipse, if k=∞, the shape becomes a rectangle. According to classical plate theory, it can be assumed that the displacement fields are:
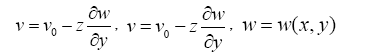(2)
in which u, v and w are total displacements, 0 u and 0 v are mid-plane displacements in the x and y directions, respectively. Considering nonlinear von Kármán strain-displacement relationships, the strains can be expressed by:
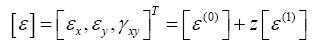(3)
in which,
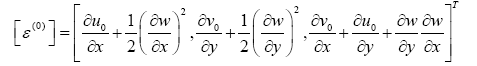(4a)
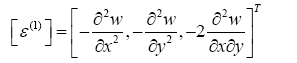(4b)
where [ε] are normal strains, and [ε(i)] (i=0,1) are components of normal strains, respectively. According to Hooke’s law, the stresses can be determined as:
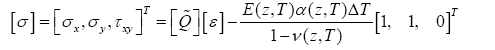(5)
Where [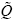
] are the transformed elastic constants, defined by:
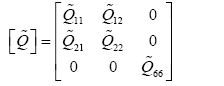(6)
And,
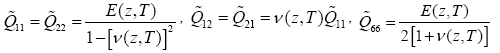(7)
The constitutive equations can be deduced by proper integration.
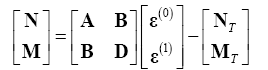(8)
Where,
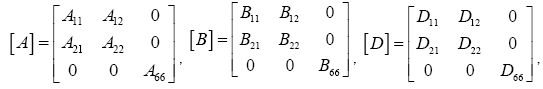
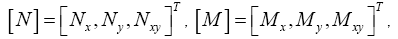(9)
In eqn. (8) the stiffnesses of the plate are defined by:
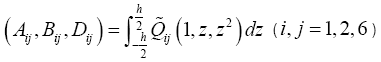(10)
The forces and bending moments caused by elevated temperature are defined by:
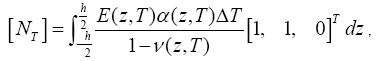
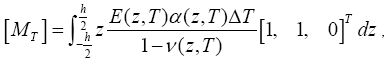(11)
Where ΔT = T −T0 is temperature rise from some reference temperature T0 at which there are no thermal strains. In the following analysis, two cases of boundaries will be considered.
u0 = v0 = w0 = Mn =0 , (for immovable simply supported edge) (12a)
u0 = v0 = w0 =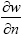 
= 0, (for immovable clamped edge) (12b)
where n refers to the normal directions of the plate boundary.
Ritz Method for Approximate Solutions of Nonlinear Problems of FGM Super Elliptical Thin Plates
Ritz method is adopted in this section to obtain approximate solutions of FGM super elliptical plates with k=2. The key issue is first to assume the deflection of the plate, and for symmetry problems about the plate with immovable simply supported edge, it can be assumed that:
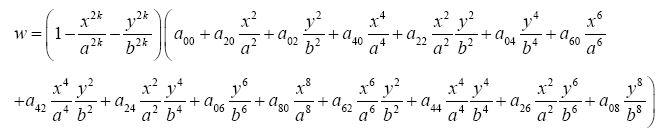(13a)
and mid-plane displacements u0 and v0 are:
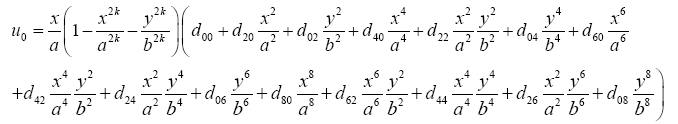(13b)
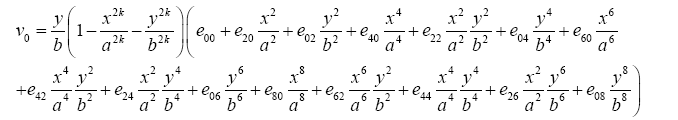(13c)
For symmetry problems about the plate with immovable clamped edge, it can be assumed that:
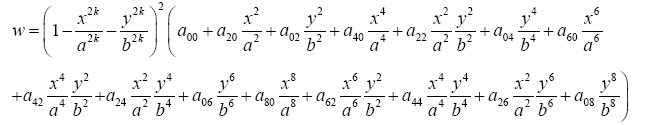(14)
and mid-plane displacements u0 and v0 have the same forms as eqns. (13b) and (13c). Note that aij , dij and eij are undetermined coefficients, and eqns. (13) and (14) satisfy displacement boundary conditions. In addition, eqns. (13) and (14) are adapted to analysis of symmetry buckling mode, but not adapted to asymmetry modes, so asymmetry modes are not discussed in this paper.
Nonlinear algebraic equations about aij , dij and eij can be obtained by substituting w , u0 and v0 into the following expression.
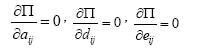(15)
in which Π =U+V , and the strain energy is:
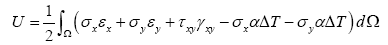(16a)
Work done by applied forces is:
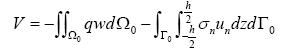(16b)
Where Ω denotes domain of FGM plates, Ω0 denotes mid-plane of FGM plates, and Γ0 denotes boundary of FGM plates.
As for FGM plates with given loads (like transverse uniformly distributed loads q0 and thermal loads ΔT ) and other known coefficients, aij , dij and eij can be solved by Newton-Raphson method or other equivalent methods. Substituting these coefficients back into eqns. (13) and (14), w , u0 and v0 may then be completely determined. In addition, critical thermal buckling loads can be easy obtained by making solutions of coefficients aij , dij and eij approach to zero.
Numerical results are presented in this section for nonlinear behaviors of FGM super elliptical plates. The effective material properties P of FGMs, such as Young’s modulus E, Poisson’s ratio v, thermal conductivity k and thermal expansion coefficient α, can be expressed as:
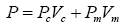(17)
in which Vm and Vc are the metal and ceramic volume fractions and are related by 1 m c V V + = , Pm and Pc denote the temperature-dependent properties of metal and ceramic plate, respectively, and may be expressed as a nonlinear function of temperature [19].
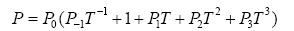(18)
in which T= T0+ ΔT and T0 =300 K (room temperature), P−1 , P0 , P1 , P2 and P3 are the coefficients of temperature T (K) and are unique to the constituent materials. Typical values for Young’s modulus E (in Pa), Poisson's ratio v, thermal expansion coefficient α (in /K) and thermal conductivity k (in W/mK) of Si3N4 and SUS304 are listed in Table 1 [20].
| Material | Properties | P-1 | P0 | P2 | P2 | P3 |
|---|---|---|---|---|---|---|
| Si3N4 | E (Pa) | 0 | 348.43e+9 | -3.070e-4 | 2.160e-7 | -8.946e-11 |
| ν | 0 | 0.24 | 0 | 0 | 0 | |
| α(1/K) | 0 | 5.8723e-6 | 9.095e-4 | 0 | 0 | |
| κ(W/mK) | 0 | 13.723 | -1.032e-3 | 5.466e-7 | -7.876e-11 | |
| SUS304 | E (Pa) | 0 | 201.04e+9 | 3.079e-4 | -6.534e-7 | 0 |
| ν | 0 | 0.3263 | -2.002e-4 | 3.797e-7 | 0 | |
| α(1/K) | 0 | 12.330e-6 | 8.086e-4 | 0 | 0 | |
| κ(W/mK) | 0 | 15.379 | -1.264e-3 | 2.092e-6 | -7.223e-10 |
Table 1. Temperature-dependent coefficients for ceramic and metals [20].
One dimensional temperature field is assumed to be constant in the x-y plane of the layer in respect that temperature variation is uniform or occurs in the thickness direction only. In such a case, the temperature distribution along the thickness can be obtained by solving a steady-state heat transfer equation:
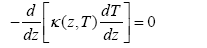(19)
This equation can be solved by imposing boundary condition of T = Tt at the top surface ( z = − h / 2 ) and T = Tb at bottom surface ( z = − h / 2). The solution of this equation is:
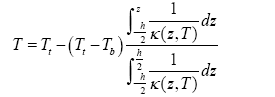(20)
Note that the temperature field is uniform when Tt = Tb .
The accuracy and effectiveness of the present method can be seen in the previous works [17,18,21,22]. Comparison results of non-linear bending and non-linear free vibration of super elliptical isotropic thin plates can be seen in refs. [17,18] and comparison results of non-linear bending and thermal post-buckling analysis of FGM elliptical plates can be seen in refs. [21,22]. Excellent agreements of comparison results [17,18,21,22] can be obtained. Thus, comparison results are omitted in this paper. In addition, in order to obtain suitable accuracy, investigations on FGM super elliptical plates need more series than FGM elliptical plates.
A parametric study was undertaken for nonlinear bending of Si3N4/SUS304 super elliptical plates with a / b =1 and a /h=15 , the power of the super ellipse k = 2 , the volume fraction Vc is defined by Vc= (1/2 - z/h)N, and the non-dimensional transverse uniformly distributed loads is defined by q0a4 / E0h4, E0is Young’s modulus of SUS304 at reference temperature. The top surface is ceramic-rich, whereas the bottom surface is metal-rich, hence Tt = Tc and Tb = Tm for heat conduction.
The maximum dimensionless deflections of Si3N4/SUS304 FGM super elliptical plates with immovable simply supported edge and immovable clamped edge subjected to transverse uniformly distributed loads in different temperature fields are calculated. It can be concluded that the deflections increase with increasing value of mechanical loads in Figures 2-7, and subjected to the same mechanical loads, the deflections increase with increasing value of volume fraction index N in Figure 2 and 5 and increasing value of temperature rise in Figure 3 [5,6]. Without mechanical loads, downward initial deflections in Figure 3 and the upward initial deflections in Figure 4 can be observed for the plates with immovable simply supported edge, while no initial deflections can be observed for the plates with immovable clamped edge in Figures 6 and 7.
Figure 2: Nonlinear bending behaviors of Si3N4/SUS304 super elliptical plates with immovable simply supported edge in room temperature fields.
Figure 3: Effect of uniform temperature rise on the nonlinear bending behaviors of Si3N4/SUS304 super elliptical plates with immovable simply supported edge.
Figure 4: Effect of heat conduction on the nonlinear bending behaviors of Si3N4/SUS304 super elliptical plates with immovable simply supported edge.
Figure 5: Nonlinear bending behaviors of Si3N4/SUS304 super elliptical plates with immovable clamped edge in room temperature fields.
Figure 6: Effect of uniform temperature rise on the nonlinear bending behaviors of Si3N4/SUS304 super elliptical plates with immovable clamped edge.
Figure 7: Effect of heat conduction on the nonlinear bending behaviors of Si3N4/SUS304 super elliptical plates with immovable clamped edge.
Thermal post-buckling behaviors for Si3N4/SUS304 FGM super elliptical plates with immovable simply supported edge and immovable clamped edge subjected to uniform temperature rise and heat conduction are calculated, Figures 8-11. Bifurcation of buckling can occur for isotropy plates with immovable simply supported edge due to effect of uniform temperature rise in Figure 8 and for FGM plates with immovable clamped edge in Figures 10 and 11, while bifurcation of buckling can’t occur for FGM plates due to effect of uniform temperature rise in Figure 8 and for both isotropy plates and FGM plates due to effect of heat conduction in Figure 9. And it can be observed that critical thermal bucking loads decrease with increasing the value of volume fraction index N for FGM plates with immovable clamped edge in Figures 10 and 11.
Figure 8: Thermal post-buckling behaviors for Si3N4/SUS304 super elliptical plates with immovable simply supported edge subjected to uniform temperature rise.
Figure 9: Thermal post-buckling behaviors for Si3N4/SUS304 super elliptical plates with immovable simply supported edge subjected to heat conduction.
Figure 10: Thermal post-buckling behaviors for Si3N4/SUS304 super elliptical plates with immovable clamped edge subjected to uniform temperature rise.
Figure 11: Thermal post-buckling behaviors for Si3N4/SUS304 super elliptical plates with immovable clamped edge subjected to heat conduction.
In this paper, nonlinear bending and thermal post-buckling analysis are first presented for functionally graded super elliptical plates with k=2 based on classical plate theory. Material primary parameters are assumed to be temperature-dependent and vary along the thickness. Ritz method is employed to analyze nonlinear bending and thermal post-buckling behaviors. Numerical results are for Si3N4/SUS304 plates, and confirm that the characteristics of nonlinear bending and thermal post-buckling are significantly influenced by different boundary conditions, thermal environmental conditions, as well as volume fraction index.