Numerical Study of Alloy/Nanocomposite-based Solar Selective Absorber with High Photo-Thermal Conversion Efficiency

Abstract

Based on the four-layered metal/dielectric film structure with high optical absorption in the 400-1000 nm spectral range, a new four-layered film structure has been studied and designed to improve the optical absorption with the spectral range being expanded to 250-1600 nm. After analyzing the advantages and disadvantages of the different metals and dielectric materials, the most suitable materials for this film structure have been chosen. In terms of Bruggeman model, the optimized optical constant of alloys has been carefully analyzed to achieve the best solar absorption performance of the SSA device. Afterwards, Maxwell Garnett model was used to fit the optical constants of the metal-dielectric material, which satisfies the conditions and properties of the SSA device required in applications.

Keywords

Solar energy, Photon-to-heat conversion, Multilayer film structure, Alloy, Nanocomposite, Bruggeman model, Maxwell Garnet model

Introduction

With decreasing of traditional energy sources and enhancement of environmental awareness, as an abundant renewable energy resource, solar energy is changing all aspects of life. Solar-to-thermal conversion, commonly viewed as Concentrating Solar Power (CSP), is another promising solar energy conversion technology except for solar-to-electric conversion. Without the traditional heat engines in the CSP, direct heat-to-electricity conversions, mainly regarding as the solar thermoelectric generator (STEG) and solar thermophotovoltaics (STPV), have attracted great scientific interest [1,2]. With development of solar thermal conversion technology, the selective solar absorber (SSA) which plays the key role in the solar thermal conversion, is of great importance.

According to previous studies, six types of SSAs have been proposed: intrinsic absorbers, semiconductor-metal tandems, multilayer absorbers, cermet absorbers, textured absorbers and photonic crystals [1-3]. All these six types of SSAs have the two main features: maximize the solar absorption in the solar spectrum region and minimize the radiation emission in the thermal infrared region. According to Kirchhoff’s law, to minimize the emission in the thermal infrared region means to minimize the absorption in this region. To summary, an ideal SSA will serve as a completely absorber in the solar region and at the same time as a completely reflector in the thermal infrared region. Among these six types of SSAs, cermet absorbers have been studied most intensively in past decades. With the good thermal stability, cermet absorbers are still limited for absorptivity in the absorption spectral region, due to the sensitivity to chemical reactions [4-6]. For example, the up-to-date study [7] has shown one kind of SS/TIC-Y/Al₂O₃ cermet absorber with the absorption of about 90%. As compare to the traditional cermet-based SSA device, multilayer absorbers show the merits of stable thermal properties, optimally designed structure, high and uniform absorption in the broad spectral region, and low thermal emittance in the infrared region. The typical nano-Cr-film-based four-layer solar selective absorber has been verified with the absorption higher than 95% in the wavelength region of 400-1200 nm [8]. A follow-up study investigated the 6-layered film structure with good absorption higher than 95.5% in the 250-1200 nm spectral region by the experiments [9]. These early studies, however, had ignored about 8% solar energy in the near-ultraviolet and near-infrared spectral region. Due to the intrinsic optical constants of the absorbing materials existing in the nature, it tends to add more absorbing layers to harvest more solar energy in a much wider solar radiation spectral region. With more layers, the production cost will increase, however. Based on the typical four-layered metal/dielectric film structure, we focus on the study and design of the new four-layered film structure to improve the optical absorption with the spectral range being expanded to about 250-1600 nm without adding additional layers in the SSA structure.

Method

To optimize the four-layered SSA, all numerical simulations must obey the law of photon energy conservation. By ignoring some trivial factors, the general equation T+A+R=1 should be satisfied, where T, A and R are transmissivity, absorptivity and reflectivity, respectively, depending on the wavelength of λ. Due to the metal reflector which is quite thick in the structure, the transmissivity T will be equal to zero so that it could be ignored.

All our simulations are carried out by using the Film Wizard software. There are some methods to calculate the energy transmission in the multilayered structure. Among different methods, plane wave expansion method, mainly based on expanding electromagnetic field in the form of plane wave, is one of effective approach used frequently in early days. By turning Maxwell’s equations into eigen functions, the eigen frequency of the transmitting photon could be obtained in terms of eigenvalues. There is the disadvantage of fixed dielectric constants to make the plane wave expansion method be inferior to the transfer matrix method. By turning Maxwell’s equations into the form of transfer matrix, the transfer matrix method has the advantage to expand the electromagnetic field in the real lattice space. It is suitable for the metal system by changing dielectric constants with respect to different wavelength. So in the follow-up study, the numerical calculation will be carried out by using the transfer matrix method.

Then, to be closer to the practical situation, the average solar illuminance on the earth surface is chosen as the spectral weight in the simulation under the condition of AM1.5 G (air mass=1.5) solar radiation spectrum of Lsun. According to the requirements of the efficient SSA, absorptivity and thermal emittance will be the key factors to influence the performance of the SSA structure under certain operation temperature T. The absorptivity is calculated by the following equation [8]:

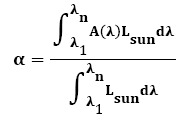
The thermal emittance can be evaluated by the reflectivity R(θ,λ) and Plank’s black body radiation E(T, λ) to have the expressions as that:

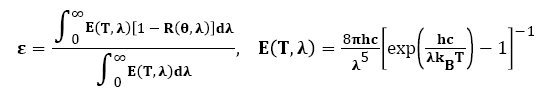
Where θ is the incidence angle of radiation.

According to the condition as mentioned above, the designed four-layered SSA will be based on the structure in our previous studies as shown in Figure 1. With the layered structure, each layer of the SSA is assumed to be relatively independent. The top layer is the anti-reflection (AR) layer to protect the multilayer structure working under the air atmosphere condition. The second layer is the absorber layer, mainly to absorb the solar radiation in the visible and near infrared region. The third layer is the transparent layer which has the function to match the amplitude and phase of the light transmitting through the layered structure. The bottom layer neighboring to the substrate is the metal reflector. Generally, Cu, Al, Au and Ag would be chosen as the reflector material. The electrical field of the transmitted solar radiation in the metal film will decay exponentially due to Lambert's law [10]:

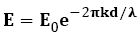
where k and d are the extinction coefficient and thickness of the metal reflector layer, respectively. Assumed d=λ/5 and k=5, then E=0.002E0. In this case, if the thickness of the metal reflector layer is set to be about 100 nm at the wavelength of 500 nm, the transmissivity T will be about 0.0004%. Therefore, the material and thickness of the reflector will not be the sensitive factor in the design so long as the metal reflector is optically thick enough. In the following discussion, aluminum will be chosen as the material of the metal reflector layer.

The influence of material changing with respect to other three layers (except for the metal reflector layer) on the solar absorptivity of the SSA is then studied. Generally, the material of the top layer and the third layer was set to be the same dielectric medium. The dielectric materials should have a relatively broad bandgap, implying that it will be difficult for the bound electron in the valence band to be excited into to the conduction band, to make the dielectric materials be totally transparent in the visible and near infrared region. With such characteristics, stable dielectric materials are used for the top and third layers to match the optical phase and amplitude with the absorption layer, but the material chosen for these two layers is not a critical factor in the design. By concerning of the simpler structure fabrication and practical application, the material of the top and third layers can generally be set as the same dielectric medium. There are various dielectric materials to satisfy the condition in the nature and to be suitably used as for the AR coating and matching layers. Some common dielectric materials, such as MgF₂, Si₃N₄, Al₂O₃, CaF₂, KCl, SiO₂, TiO₂ and so on can be chosen in the design.

To improve the solar selective absorptivity under operation temperature, the material of the absorber layer with proper optical constants and thickness is the key part in the SSA structure. Alloys and nanocomposite materials are then considered to be the absorption materials.

According to the previous study, typical transition metals, like Cr, Ti, W and Fe, present the optical property of strong absorption in the broad spectral region. By considering these transition metals, six types of alloys are proposed, namely Cr-Ti, Cr-W, Cr-Fe, Ti-W, Ti- Fe and W-Fe. Alloys are assumed to have the spectrally suitable absorption pattern better than the element metal in expectation. Bruggeman model, reduced from the Effective Media Approximation (EMA) model, is used to fit the optical constants of the alloys. As for the method to treat the optical constants of heterogeneous and composite materials, the EMA model assumes the composite as an effective medium with the required dielectric constants in the specific region of spectrum. As one kind of EMA model, Bruggeman model assumes randomly mixed grains of two materials with the result obtained in self-consistent data analysis. The dielectric constants of the finally composited material are set to be equal to that of the host material. Bruggeman model was used to fit the optical constants of Al-Cu alloys suitably in early studies [11] with the equation given below [12]:

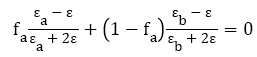
Where, f_a and (1-f_a) represent the fraction of the individual medium in the composite material with the dielectric constant ε_a and ε_b, respectively.

In the next step, the nanocomposite material is set to be the absorption layer in the SSA structure. The ideal absorption materials should have the optical property of strong absorption with respect to the solar spectrum just like the metal, but should combine with the proper dielectric material to achieve low blackbody emittance in the infrared spectral range. In the study, therefore, the nanocomposite materials are composed of the host medium with the nanoparticles embedded inside as shown in Figure 2. In the data analysis, Maxwell Garnett Model, another type of EMA model is also applied to fit the optical constants of nanocomposites. Usually, except for the Maxwell Garnett Model, Mie’s theory, introducing the spherical boundary condition into Maxwell equations, can be used to well describe the absorption and emission of the single particle. Under the condition of the single-particle assumption, however, Mie’s theory seems to be not working well to properly describe the interaction of particles in the nanocomposite structure. On the contrary, Maxwell Garnett model, introducing the particle-particle interaction to modify the dielectric constant induced by the host material, seems to be more suitable to describe the optical properties of nanocomposite materials [13,14]. Set εh and εnp to be the dielectric constant of host medium and nanoparticles, respectively, the Maxwell Garnett model is given as follows:

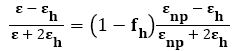
Based on the Maxwell Garnett theory, different transition metals were chosen as the host medium in which the nanoparticles of the dielectric material will be embedded. The optical constants of the materials with respect to the solar radiation spectrum were input from Handbook of Optical Constants of Solids [15].

Under the consideration and condition as mentioned above, the optimization for two types of SSA structures was carried out by Global Modified Levenberg-Marquardt. As one kind of Global Gradient Methods, Global Modified L-M method is accomplished by starting optimization process in different regions and keeping track of root-mean-squareerror of each solution, without falling into local minima. Root-mean-square-error (RMSE) was also used to evaluate the optimization results. The thickness of three layers and the percentage of the element material in the nanocomposite were set to be variables under the above-mentioned conditions, and the least RMSE would be sought by Global Modified L-M method under various trials. With the fixed optical constants of the specific material, changing of thickness for each layer will tune the optical phase and amplitude of the light propagating in the structure, resulting in an optimal optical property of the whole SSA in the design.

Results and Discussions

The four-layered structure studied previously [8] has an optimized absorptivity higher than 95% in the 400-1200 nm wavelength region. But in the region between 250 nm and 400 nm, the mismatching of optical phase and optical amplitude occurs obviously, as shown in Figure 3, resulting in the weighted average absorptivity of about 85% in the 250-1600 nm wavelength region with respect to the solar spectrum AM1.5G under the normal incidence condition. At the same time, the value of optimization RMSE calculated in the 250-1600 nm wavelength region is about 17, implying there’s still plenty of room for the structure to be improved.

Based on the Bruggeman model, by using the same materials of the reflector and transparent layers, the structures with different alloys serving as the absorption layer were optimized under the normal incidence condition. Figure 4a shows the absorptivity of six structures calculated with Ti-W, Ti-Fe, Cr-Fe, Cr-W, W-Fe or Ti-Cr alloys. Obviously, the RMSE of these six structures is greatly improved to show that the absorption layer composed by the alloys will make the SSA structure have better optical performance than the one composed by the pure element metals. By comparison, the SSA with the Ti-W alloy layer has the lowest value of RMSE among these six structures. The optimized 4-layered SSA structure is SiO₂ (79 nm)/Ti66W34 (14 nm)/SiO₂ (65 nm)/Al (≥100 nm), and the optimization weighted average absorptivity in the 250-1600 nm wavelength region is enhanced to the value of about 88%. The mismatching of optical phase and amplitude still exists in the ultraviolet region. In terms of the complex refractive index ñ (complex dielectric constant ε=ñ²), the real (n) and imaginary (k) of ñ(ñ=n+ik) are the refractive index and extinction coefficient of the material to characterize mainly the phase changing and absorption of the light propagating in the metal layer, respectively.

The imaginary parts of six types of alloys, given in Figure 4b, show the increasing tendency with the wavelength. The value of imaginary part of the complex refractive index in the ultraviolet region is relatively smaller than that in the long wavelength region.

In the assumption that the metal-dielectric nanocomposites will produce the effective optical constant interpreted by both of the metal and dielectric materials, therefore, nanocomposites were designed to be the key absorption layer in the four-layered SSA structure. After amounts of simulations, the nanocomposite using SiO₂ as the nanoparticle embedded in the Ti host medium was studied to show the best performance with the highest solar-to-thermal conversion efficiency of the four-layered SSA structure. The optimized structure is SiO₂ (53 nm)/Ti-SiO₂ (700 nm)/SiO₂ (2 nm)/Al (≥100 nm). Each layer in the structure is thick enough and the optical constant of the layer will not be significantly affected by the size effect. By spherical approximation of the nanoparticle, the optimized fraction of SiO₂ nanoparticles embedded in the host medium is about 89%. The higher absorptivity with the structure under the normal incidence conduction is shown in Figure 5a. The calculated weighted average absorptivity in the 250-1600 nm wavelength region is about 97.7%, much higher than that of the early-studied structure. With enough trials, the weighted average absorptivity in calculation is almost unchanged within the thickness deviation of each layer being less than 1 nm. The optimization structure then can be physically feasible for the structure fabrication and application. The mismatching effect of optical phase and amplitude in the structure in the ultraviolet region has been significantly minimized without decreasing of absorptivity in the long wavelength region. Optical constants of the composite material are shown in Figure 5b. The nanocomposite with SiO₂ as nanoparticle and Ti as the host medium has the relatively linear extinguish efficient in the region between 250 nm and 1600 nm. The refractive index n and extinction efficient k have the numerical values of less than 2 and 1, respectively, in the entire 250-1600 nm wavelength region. With the relatively smaller k values of Ti-SiO₂ nanocomposite, the thickness of the absorption layer required for the SSA structure will be thicker than that of alloys or element metal layers. As shown in Figure 5c and 5d, the change of incident angle will influence the absorptivity. When the incident angle is in the range of less than 60°, however, the absorptivity of the SSA structure will be less affected by the variation of the incident angle.

Obviously, the Ti-SiO₂ composite is better than the natural metal materials to be used as the absorbing materials in the four-layered SSA structure, especially in the ultraviolet and infrared regions. This can be explained according to the optical properties of solids, since the dielectric constant of metal can be well characterized by Drude model in the low energy region where the intraband transition of free electrons will dominate the optical properties of the metal. In the higher energy region where the interband transition happens, however, the dielectric constant of metal has to be described by the Lorentz oscillator model [16]. Due to intraband transition in the Drude region, therefore, metals will have strong absorption property. Nevertheless, electrons will be constrained by the atomic nucleus to make the weak optical absorption in the ultraviolet region. The Ti-SiO₂ composite may provide a mechanism to balance the absorption properties with respect to the broad solar spectral region. This can be supported by the calculated results to show the best solar-to-thermal performance of the four-layered SSA structure using Ti-SiO₂ nanocomposite as the absorption layer, instead of using Ti-Fe and Cr as the absorption layers.

Another important factor to evaluate the performance of the SSA structure is the value of emittance, which can be reduced by reflectivity and Plank’s blackbody radiation. The emittance of the four-layered SSA structure using Ti-SiO₂ composite as the absorption layer seems to be low in a wide incident angle range and at proper temperature with the data shown in Table 1. The emittance of the optimized SSA structure is slightly higher than that of the early-studied multilayer structure, but really gets improved by comparing to that of the cermet structure [2]. With relatively low emittance in the low and middle temperature range, the SSA device with simpler structure can be fabricated to potentially satisfy for the application in the solar-to-thermal conversion system in the future.

Table 1. Calculated emittance value of the structure [SiO₂ (53 nm)/Ti-SiO₂ (700 nm)/ SiO₂ (2 nm)/Al (≥100 nm)].

Conclusion

Based on the early-studied four-layered metal/dielectric SSA structure, alloy or nanocomposite based SSA structures are proposed and studied. Ti-W alloy based SSA structure performances best among six types of alloy-based structure, which improves the absorptivity just a little in the 250-1600 nm wavelength region. On the contrary, the Ti-SiO₂ composite based SSA structure reduces significantly the mismatching effect of optical phase in the ultraviolet region without decreasing of the absorption in the long wavelength region. Compared to the six-layered SSA structure, the simpler four-layered structure [SiO₂ (53 nm)/Ti-SiO₂ (700 nm)/SiO₂ (2 nm)/Al (≥100 nm)] has the weighted average absorptivity of 97.7% and relatively low emittance at the low and middle operation temperature. So the optimized SSA structure will be cost-effective and has great potential to feasibly put into application in the future.

Acknowledgement

This work is supported by the National Natural Science Foundation of China under project No. 61427815 and No. 61274054.

References

1. Kennedy CE. Review of Mid- to High-Temperature Solar Selective Absorber Materials. Sol Energy 2002.
2. Lin C and Povinelli ML. Optimal design of aperiodic, vertical silicon nanowire structures for photovoltaics. Opt Express 2011;5:A1148.
3. Weinstein LA, et al. Concentrating Solar Power. Chem Rev 2015;115:12797.
4. Zhang Q and Mills DR. New cermet film structures with much improved selectivity for solar thermal applications. Appl Phys Lett 1992;60:545-547.
5. Zhang J, et al. Modeling of a selective solar absorber thin film structure based on double TiNxOy, layers for concentrated solar power applications. Sol Energy 2017;142:33-38.
6. Okuhara Y, et al. Solar-selective absorbers based on semiconducting β-FeSi2, for efficient photothermal conversion at high temperature. Sol Energy Mater Sol Cells 2017;161:240-246.
7. Gao XH, et al. Enhanced thermal stability and spectral selectivity of SS/TiC-Y/Al2O3 spectrally selective solar absorber by thermal annealing. Sol Energy 2016;140:199-205.
8. Zhou WX, et al. Nano-Cr-film-based solar selective absorber with high photo-thermal conversion efficiency and good thermal stability. Opt Express 2012;20:28953.
9. Liu MH, et al. High efficiency of photon-to-heat conversion with a 6-layered metal/dielectric film structure in the 250-1200 nm wavelength region. Opt Express 2014;7:A1843.
10. Palik ED. Handbook of Optical Constants of Solids. Academic Press 1985.
11. Barron LW, et al. Optical, electrical, and structural properties of sputtered aluminum alloy thin films with copper, titanium and chromium additions. Thin Solid Films 2007;515:3363-3372.
12. Fujiwara H. Spectroscopic Ellipsometry: Principles and Applications. John Wiley & Sons Ltd 2007:1-11.
13. Maxwell Garnett JC. Colours in Metal Glasses and in Metallic Films. Philos T Roy Soc A 1904;203:385-420.
14. Belahmar A and Chouiyakh A. Size and Concentration Effects on Surface Plasmon Resonance and Maxwell-Garnett Absorption in RF-Magnetron Sputtered Au/Al2O3 Nanocomposite Films. J Thin Films Res 2017;1:1-6.
15. Palik ED. Handbook of optical constants of solids. J Mod Opt 1991;39:189.
16. Chang SH, et al. Surface plasmon generation and light transmission by isolated nanoholes and arrays of nanoholes in thin metal films. Opt Express 2005;13:3150-3165.