ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
R.Muthucumaraswamy1, B.Saravanan2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
The objective of the present work is to study the heat and mass transfer effects on unsteady MHD radiative flow past an oscillating semi-infinite isothermal vertical plate with uniform mass flux. The fluid considered here is a gray, absorbing-emitting radiation but non-scattering medium. The dimensionless governing equations are solved by an efficient, more accurate, and unconditionally stable and fast converging implicit scheme. The effect of velocity, concentration and temperature for different parameters like thermal radiation, magnetic field, Schmidt number, thermal Grashof number and mass Grashof number are studied. It is observed that the velocity decreases in the presence of thermal radiation or magnetic field parameter
Keywords |
| MHD, radiation, isothermal, vertical plate, finite-difference, mass flux |
INTRODUCTION |
| The study of flow problem, which involve the interaction of several phenomena, has a wide range of applications in the field of science and technology. One such study is related to effects of free convection MHD flow, which plays an important role in agriculture, petroleum industries, geophysics and astrophysics. Also it has applications in the field metrology, solarphysics, aeronautics, chemical engineering and electronics. The effect of Radiation on MHD flow and heat transfer problems have been more important industrially. The subject of magneto hydrodynamics has attracted the attention of large number of researchers due to its diverse application. In astrophysics and geophysics it is used to study the stellar and solar structures, etc. In engineering, it is used in MHD pumps and MHD bearing, etc. Soundalgekar , Gupta and Aranake[1] have studied Free convection currents on MHD Stokes problem for a vertical plate. England and Emery [2] have studied the thermal radiation effects of a optically thin gray gas bounded by a stationary vertical plate. Soundalgekar , Gupta and Birajdar have studied the Effects of Mass transfer and free convection currents on MHD Stokes problem for a vertical plate[3]. Soundalgekar and Takhar [4] have considered the radiative free convective flow of an optically thin gray-gas past a semiinfinite vertical plate. Radiation effect on mixed convection along a isothermal vertical plate were studied by Hossain and Takhar [5]. Raptis and Perdikis [6] have studied the effects of thermal radiation and free convection flow past a moving infinite vertical plate. Again, Raptis and Perdikis [7] studied thermal radiation effects on moving infinite vertical plate in the presence of mass diffusion. The flow of a viscous, incompressible fluid past an infinite isothermal vertical plate, oscillating in its own plane, was studied by Soundalgekar [8]. The effect on the flow past a vertical oscillating plate due to a combination of concentration and temperature differences was studied extensively by Soundalgekar and Akolkar [9]. The effect of mass transfer on the flow past an infinite vertical oscillating plate in the presence of constant heat flux has been studied by Soundalgekar et al[10]. Shanker and Kishan[11] have studied the effect of mass transfer on the MHD flow past an impulsively started infinite vertical plate with variable temperature or constant heat flux. MHD Stokes problem for a vertical infinite plate with variable temperature was studied by Soundalgekar, Patil and Jahagirdar[12]. Singh and Sacheti[13] have studied the Finite difference analysis of unsteady hydromagnetic free-convection flow with constant heat flux. Numerical solution on natural convection along an oscillating isothermal vertical plate under the combined buoyancy effects of heat and mass diffusion in the presence of thermal radiation has not received attention of any researcher. This study found useful in distribution of cooling in a closed environment. Hence, the present study is to investigate the unsteady flow past an oscillating semi-infinite vertical plate with thermal radiation by an implicit finite-difference scheme of Crank-Nicolson type. |
II. MATHEMATICAL FORMULATION OF THE PROBLEM |
| A transient, laminar, unsteady natural convection flow of a viscous incompressible fluid past an oscillating semi-infinite isothermal vertical plate in the presence of thermal radiation has been considered. It is assumed that the concentration C' of the diffusing species in the binary mixture is very less in comparison to the other chemical species which are present. Here, the x-axis is taken along the plate in the vertically upward direction and the y-axis is taken normal to the plate. The physical model of the problem is shown in figure 1. Initially, it is assumed that the plate and the fluid are of the same temperature and concentration. |
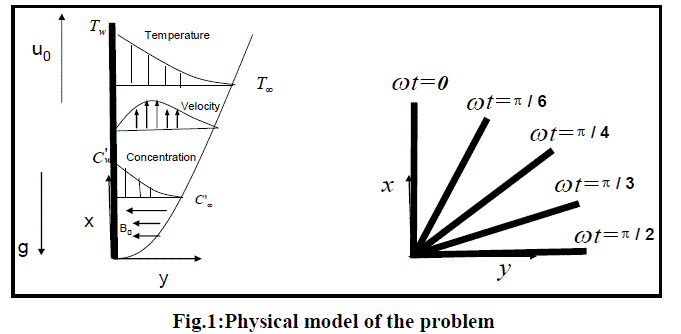 |
| At time tï¢ > 0 , the plate starts oscillating in its own plane with frequency ï·ï¢ against gravitational field. The temperature of the plate is raised w T and the concentration level near the plate is raised at a constant rate. The fluid considered here is a gray, absorbing-emitting radiation but a non-scattering medium and the viscous dissipation is assumed to be negligible. Then under the above assumptions, the governing boundary layer equations of mass, momentum and concentration for free convective flow with usual Boussinesq’s approximation are as follows(Gebart and Pera[14]): |
 |
 |
 |
| calculation. The coefficients , n i j U and , n i j V appearing in the finite difference equation are treated as constants at any one time step. Here i-designates the grid point along the X - direction, j along the Y- direction and k to the t-time. The values of U, V and T are known at all grid points at t = 0 from the initial conditions. The computations of U, V , T and C at time level (n +1) using the values at previous time level (n) are carried out as follows: The finite-difference equations (3.4) and (3.7) at every internal nodal point on a particular i-level constitute a tridiagonal system of equations. The system of equations is solved by using Thomas algorithm as discusses in Carnahan et al [11]. Thus, the values of C are found at every nodal point for a particular i at (n+1)th time level. Similarly, the values of T are calculated from equation (3.3) .Using the values of C and T at (n+1)th time level in the equation (3.2) , the values of U at (n+1)th time level are found in a similar manner. Thus, the values of C, T and U are known on a particular i-level. Finally, the values of V are calculated explicitly using the equation (3.1) at every nodal point at particular i-level at (n+1)th time level. This process is repeated for various i-levels. Thus the values of C, T, U and V are known, at all grid points in the rectangle region at (n+1)th time level. In a similar manner computations are carried out by moving along i-direction. After computing values corresponding to each i at a time level, the values at the next time level are determined in a similar manner. Computations are repeated until the steady-state is reached. The steady-state solution is assumed to have been reached, when the absolute difference between the values of U, and as well as temperature T and concentration C at two consecutive time steps are less than 10-5 at all grid points. |
IV. RESULTS AND DISCUSSION |
| The numerical values of the velocity, temperature and concentation are computed for different parameters like radiation parameter, magnetic field, Schmidt number, phase angle, thermal Grashof number and mass Grashof number. The purpose of the calculations given here is to assess the effects of the parameters ï·t, R,Gr,Gc and Sc upon the nature of the flow and transport. The value of Prandtl number Pr is chosen such that they represent air (Pr = 0.71) and the Schmidt number Sc = 0.6(Water vapour). The steady-state velocity profiles for different phase angle are shown in figure 2. The velocity profiles presented are those at X = 1.0. It is observed that for different phase angle (ï· t ï½ 0,ï° /6,ï° /3,ï° /2 ), Gr=5=Gc, M=2 and R=2 the velocity decreases with increasing phase angle. Here ωt = 0 represents vertical plate and note that the velocity profile grows from U = 1 and ï· t = ï° /2 refers horizontal plate and the velocity profiles starting with U = 0. The numerical value satisfies with the prescribed boundary conditions. It is also observed that the time taken to reach steady-state is more in the case of vertical plate than horizontal plate. |
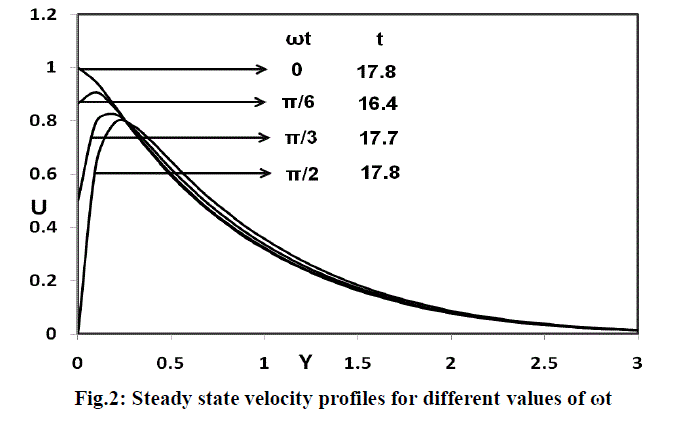 |
| In figure 3, the velocity profiles for different thermal Grashof number(Gr=2,5), mass Grashof number(Gc=2,5), ï· t ï½ ï° /6 , M=2 and R=2 are shown graphically. This shows that the velocity increases with increasing thermal Grashof number or mass Grashof number. As thermal Grashof number or mass Grashof number increases, the buoyancy effect becomes more significant, as expected; it implies that, more fluid is entrained from the free stream due to the strong buoyancy effects. |
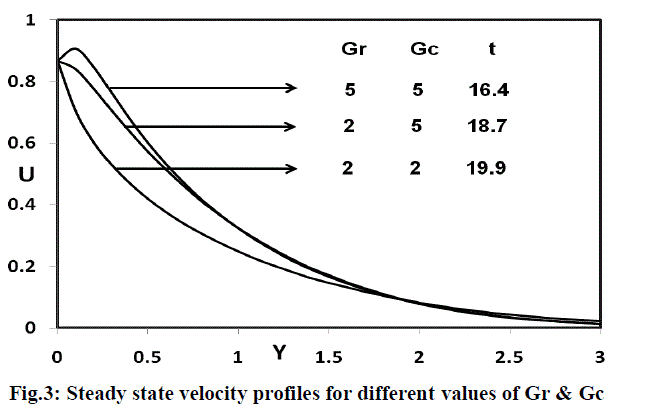 |
| The effect of velocity for different radiation parameter (R = 0.2, 2, 5, 10),ï· t ï½ ï° /6 , M=2 and Gr=Gc=5 are shown in figure 4. It is observed that the velocity increases with decreasing radiation parameter. This shows that velocity decreases in the presence of high thermal radiation. |
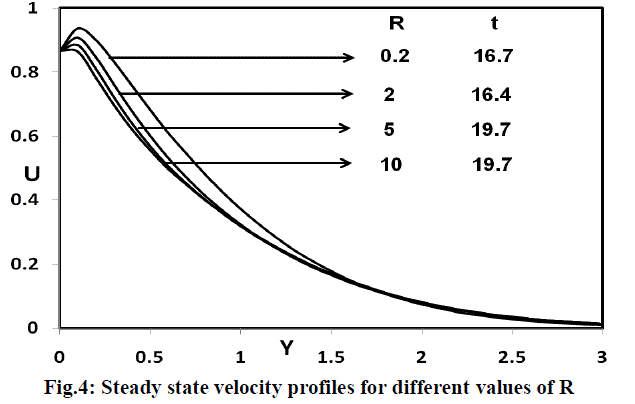 |
| The steady state velocity profiles for different magnetic parameter are shown in figure 5. It is observed that for (M=2, 5, 10), Pr=0.71, R=2 and Sc=0.6, the velocity decreases in the presence of magnetic field. This shows that the increase in the magnetic field parameter leads to a fall in the velocity. This agrees with expectation, since the magnetic field exerts a retarding force on free convection flow. |
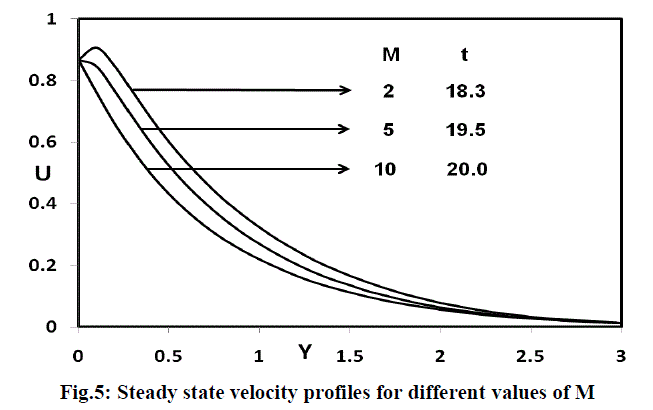 |
| The steady-state velocity profiles for different Schmidt number (Sc=0.16,0.3,0.6,2.01), Gr=Gc=5, ï· t ï½ ï° /6 , M=2 and R=2 are shown in figure 6. The velocity profiles presented are those at X = 1.0. It is observed that the velocity decreases with increasing Schmidt number and the steady-state value increases with increasing Schmidt number. The velocity boundary layer seems to grow in the direction of motion of the plate. It is observed that near the leading edge of a semiinfinite vertical plate moving in a fluid, the boundary layer develops along the direction of the plate. However, the time required for the velocity to reach steady-state depends upon the Schmidt number. This shows that the contribution of mass diffusion to the buoyancy force increases the maximum velocity significantly. |
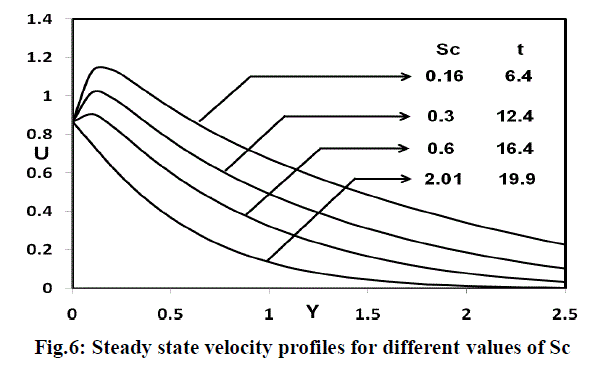 |
| The temperature profiles for different values of the thermal radiation parameter (R=0.2, 2, 5, 10) are shown in figure 7. It is observed that the temperature increases with decreasing R. This shows that the buoyancy effect on the temperature distribution is very significant in air (Pr = 0.71). It is clear that at R=0.2, the temperature increases tremendously than other radiation parameters (R=2, 5, 10). This shows that due to higher thermal radiation there is a fall in temperature. It is known that the radiation parameter and Prandtl number plays an important role in flow phenomena because, it is a measure of the relative magnitude of viscous boundary layer thickness to the thermal boundary layer thickness. |
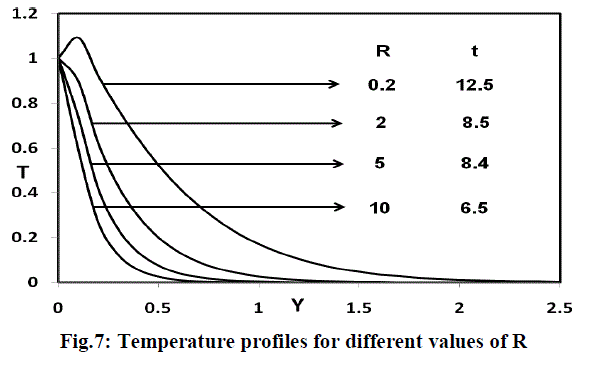 |
| The concentration profiles for different values of the Schmidt number (Sc=0.16, 0.3, 0.6, 2.01) are shown in figure 8. It is observed that the plate concentration increases with decreasing Sc. |
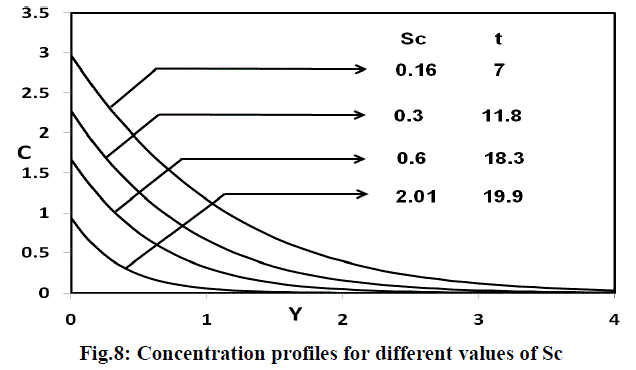 |
| Knowing the velocity and temperature field, it is customary to study the skin-friction, Nusselt number and Sherwood number. The local as well as average values of skin-friction, Nusselt number and Sherwood number in dimensionless form are as follows: |
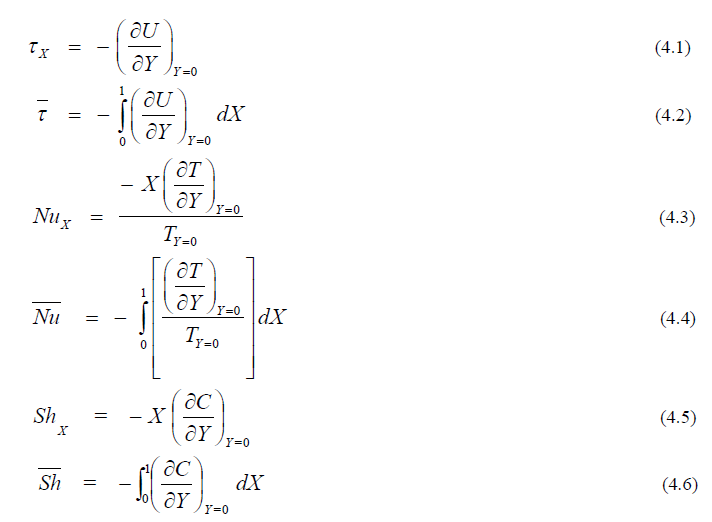 |
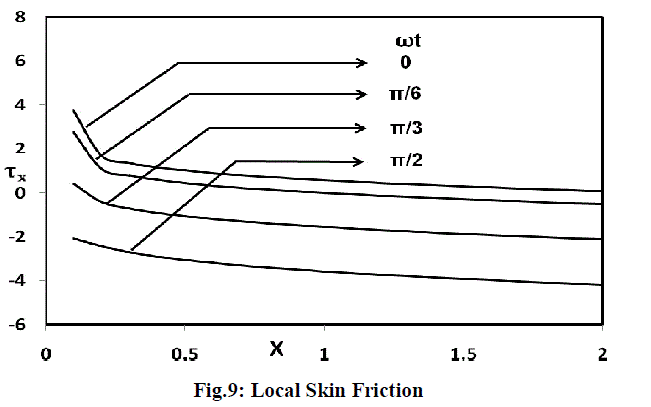
| The derivatives involved in the equations (4.1) to (4.6) are evaluated using five-point approximation formula and then the integrals are evaluated using Newton-Cotes closed integration formula. The local skin-friction, Nusselt number and Sherwood number are plotted in figures 9, 10 and 11 respectively. Local skinfriction values for different phase angle are evaluated from equation (4.1) and plotted in figure 9 as a function of the axial coordinate. The local wall shear stress increases with decreasing phase angle. The trend shows that the wall shear stress is more in the case of vertical plate than horizontal plate. |
 |
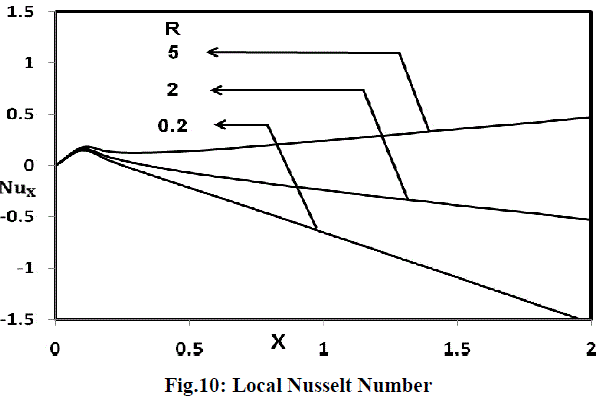
| The local Nusselt number for different thermal radiation parameter is presented in figure 10 as a function of the axial coordinate. The trend shows that the Nusselt number increases with increasing values of the thermal radiation parameter. It is clear that the rate of heat transfer is more in the presence of thermal radiation. |
 |
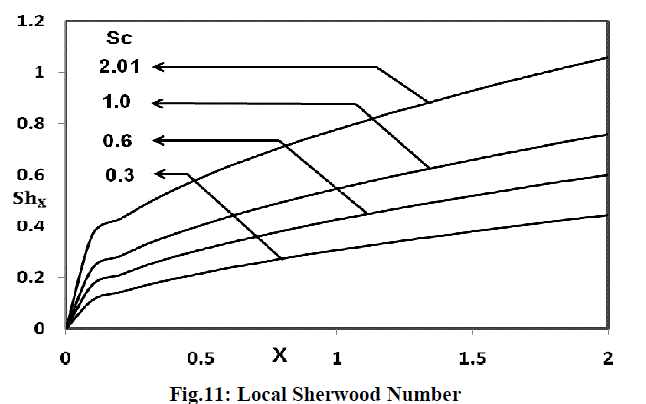
| The local Sherwood number for different values of the Schmidt number are shown in figure 11. As expected, the rate of mass transfer increases with increasing values of the Schmidt number. This trend is just reversed as compared to the concentration field for different Schmidt number given in figure 8. |
 |
| The average values of the skin-friction, Nusselt number and Sherwood number are shown in figures 12, 13 and 14 respectively. The effects of the different phase angle on the average values of the skin-friction are shown in figure 12. The average skin-friction decreases with decreasing with increasing values of the phase angle. |
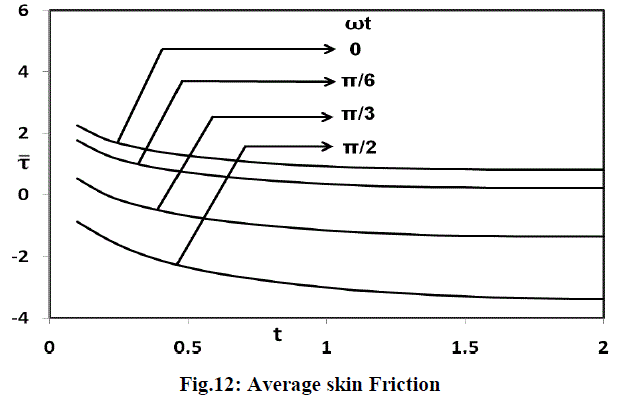 |
| Figure 13 illustrates the average Nusselt number increases with increasing radiation parameter. From the figure 14, it is observed that the average Sherwood number increases with increasing values of the Schmidt number. |
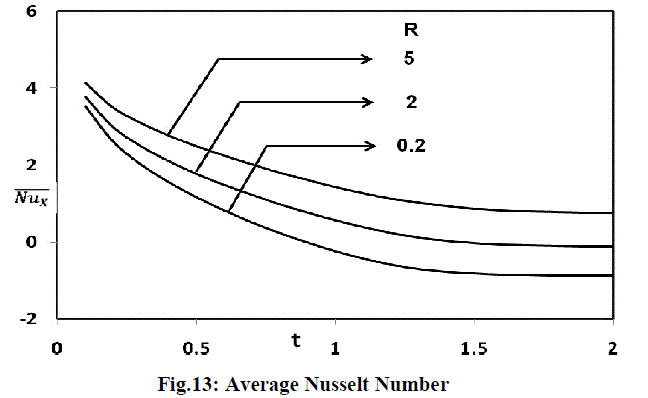 |
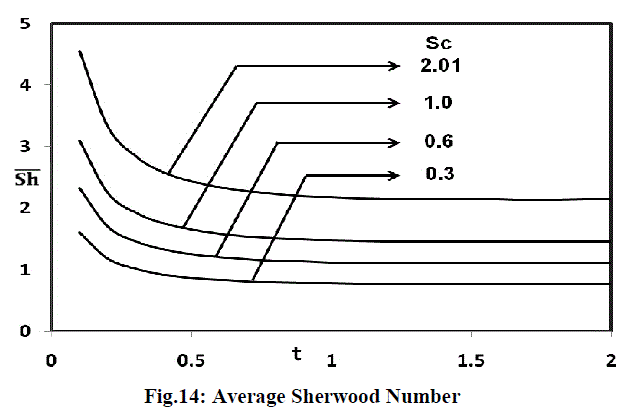 |
V CONCLUSIONS |
| The numerical study has been carried out for thermal radiation effects on unsteady flow past an oscillating semiinfinite isothermal vertical plate with prescribed uniform mass flux. The dimensionless governing equations are solved by an implicit scheme of Crank-Nicolson type. The effect of velocity, temperature and concentration for different parameter are studied. The local as well as average skin-friction, Nusselt number and Sherwood number are shown graphically. It is observed that the contribution of mass diffusion to the buoyancy force increases the maximum velocity significantly. It is also observed that the velocity decreases in the presence of thermal radiation. The study shows that the number of time steps to reach steady-state depends strongly on the radiation parameter. |
Nomenclature |
  |
References |
|