ISSN: 2319-9873
ISSN: 2319-9873
Mechanical Engineering Department, Al-Huson University College, Al-Balqa Applied University, Al-Huson- Irbid- P. O. Box 50, JORDAN
Received: 28 July 2014 Accepted: 15 May 2015 Published: 22 May 2015
Visit for more related articles at Research & Reviews: Journal of Engineering and Technology
In this study the finite element method (FEM) is used in solving the heat dissipation from a perforated fin. This fin is horizontal rectangular fin subjected to natural convection and provided with longitudinal hexagonal perforations. The orientation of these perforations is described as they have two sides parallel to the fin sides. The body of the fin is discretized into the sufficient finite elements. The number of these elements can be altered as required according to the automatic mesh generation. The heat dissipation of the perforated fin is computed and compared with that of the solid one of the same dimensions and same thermal properties. The comparison refers to acceptable results and heat dissipation enhancement due to certain perforation.
Finite element, Perforated fin, Heat dissipation, Heat transfer enhancement.
In industrial applications, the production of excess heat in the system components is unavoidable. If not adequately removed, this excess heat may have detrimental consequences on the operation of those components. In many applications, it is not possible or practicable to use cooling liquid fluids or even utilize forced gas convection where needed. It is such cases when natural convection, normally with air as the cooling medium, comes into play as the only viable cooling option. Natural convection finds very wide applications in heat exchange processes ranging from cooling of tiny electronic components to cooling of fuel elements in nuclear reactors. The utilization of natural convection in cooling processes is almost always associated with the use of extended surfaces (fins), for the sake of enhancement of the process by increasing the heat transfer area. This is especially true, and necessary, when gases are utilized as cooling media, which is dominantly the case. The reason is that gases possess convection coefficients that are an order of magnitude less than those of liquids [1]. Extended surfaces are commonly used to enhance heat transfer in many industries. There are various types of fins but rectangular plate fins are commonly used for the reason of simplicity in manufacturing [2]. Advances in heat transfer equipments such as heat sinks used in electronic devices and other systems have caused the optimization of fins as a major topic for fin design. The optimization of fins is generally based on two approaches. One is to minimize the volume or mass for a given amount of heat dissipation and the other is to maximize heat dissipation for a given volume or mass [3]. Fins are frequently used in heat exchanging devices for the purpose of increasing the heat transfer between a primary surface and the surrounding fluid. Various types of heat exchanger fins, ranging from relatively simple shapes, such as rectangular, square, cylindrical, annular, tapered or pin fins, to a combination of different geometries, have been used [4]. Compact heat exchangers are designed in configurations that have a large heat transfer surface area per unit of volume. The large area per unit of volume can be attained by attaching extended surfaces. The fins of the plate-fin surfaces are frequently cut into segments or otherwise interrupted in various ways. These modifications are for increasing the heat transfer coefficient and sometimes to increase heat transfer surface area [5,6]. It is worth mentioning that a large number of studies have been conducted to find the optimum shape of fins (rectangular, hexagonal, pin, wavy, serrated, and slotted). Some of these studies are based on splitting a certain dimension of the fin in an optimal way provided that the total volume of the fin material is fixed. Others have introduced some shape modifications by cutting some material from the fin to make cavities, holes, slots, grooves, or perforations through the fin body [7-9]. Due to the high demand for lightweight, compact, and economical fins, the optimization of fin size is of great importance [10]. Therefore, fins must be designed to achieve maximum heat removal with minimum material expenditure taking into account, however, the ease of manufacturing of the fin shape. One popular heat transfer augmentation technique involves the use of rough surfaces of different configurations. The surface roughness aims at promoting surface turbulence that is intended mainly to increase the heat transfer coefficient rather than the surface area [5]. Several other researchers reported a similar trend for interrupted (e.g. perforated) fins attributing the improvement to the restarting of the thermal boundary layer after each interruption indicating that the increase in convection coefficient is more than enough to offset lost area, if there is any [11]. The fin industry has been engaged in continuous research to reduce the fin size, weight and cost. The reduction in fin size and cost is achieved by the enhancement of heat transfer carried out by the fins. This enhancement can be accomplished by the following means:
1- Increasing the ratio of the heat transfer surface area of the fin to its volume
2- Manufacturing fins from materials having high thermal conductivity
3- Increasing the heat transfer coefficient between the fin and its surroundings
Perforated plates or perforated fins represent an example of surface interruption [7]. They are widely used for multiple-plate heat exchangers, film cooling (e.g., of turbine blades), and solar collector applications [12]. An experimental study was conducted to investigate the dissipation heat transfer by natural convection in a rectangular fin plate with circular perforations as heat sinks. In this study it is found that, the heat transfer rate and the coefficient of heat transfer increased with an increased number of perforations [13]. A three-dimensional numerical study is made for turbulent fluid flow and convective heat transfer around an array of rectangular solid and new design of perforated fins with different numbers and two various sizes of perforations. In this study, the fin efficiency of perforated fins is determined and compared with the equivalent solid fin. Results show that new perforated fins have higher total heat transfer and considerable weight reduction in comparison with solid fins [14].
The finite element method is a numerical method that can be used for the accurate solution of complex engineering problems. As the finite element technique has been so well established, it is today considered to be one of the best methods for solving a wide variety of practical problems efficiently. One of the main reasons for the popularity of the method in engineering is that once a general computer program is written, it can be used for the solution of any problem simply by changing the input data [15]. This study aims mainly to introduce a numerical finite element solution of the problem of heat transfer from a fin with longitudinal hexagonal surface perforations. This solution is restricted to the fact that the Biot Number in lateral and longitudinal directions less than 0.01.
The study of most heat transfer references shows that the classical analyses of fins employ a one-dimensional heat conduction model. As the Biot number is very small (less than 0.01), then the one-dimensional solution can be considered [16,17]. The analysis and results reported in this study are based on the following assumptions:
1. Steady-state, one-dimensional analysis
2. The fin material is homogeneous and isotropic with constant thermal conductivity
3. Uniform base and ambient temperatures
4. The surface heat transfer coefficients are uniform
The perforated fin with longitudinal hexagonal perforations which is considered in this study is shown in Figure 1.
Figure 2 shows the symmetry part considered for heat transfer analysis (shown hatched). For this part the transverse Biot number in or along the direction of z-axis ( Biz ) can be calculated by:

and the transverse Biot number in or along the direction of y-axis ( Biy ) can be calculated by

As the values of ( Biz ) and ( Biy ) are less than 0.01, then the heat transfer in (z) and (y) directions can be assumed lumped and a one-dimensional solution can be considered. If the values of ( Biz ) and ( Biy ) are greater than 0.01, then the heat transfer solution must be in two or three dimensions. In this study the parameters of the perforated fin are taken as they lead to values of ( Biz ) and ( Biy ) smaller than 0.01. Based on the above assumptions, the energy equation of the fin along with the boundary conditions and according to Figures 1-3 may be stated as below [15,18,19].

The associated boundary conditions are
1- At the base surface ( x = 0 )

2- At the perforated surfaces and the tip of the fin
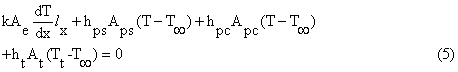
In this study, the energy equation shown in (1) is solved numerically utilizing the one dimensional finite-element technique. The corresponding variational statement as it is described in [15] has the following form:
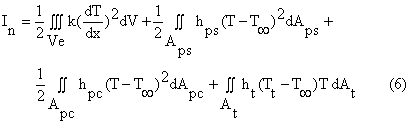
The variational approach in matrix notation [15] is used in formulating the algebraic equations of the problem of this perforated fin. The formulation of these equations can be found in details in [15]. The perforated fin elements and body discretization of the symmetry part are shown in Figures 2 and 3. As shown in Figure 3, surrounding each semi-perforation there are five regions labeled A, B, C, D and E. These regions which repeat themselves along x direction around each perforation are considered in formulating the discretization mesh and finite element equations. The regions A and E are divided into Nf elements each, while the regions B and D are divided into Nt elements each. The region C is divided into Nh elements. The perforated fin length and width can be computed by the following equations:
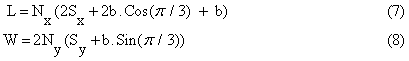
To compare the perforated fin with the solid one, their dimensions (length, width, and thickness) are considered the same. The solid and perforated fin heat transfer surfaces can be computed by the following equations:
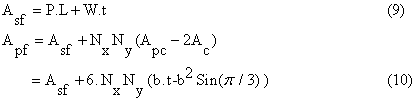
The total number of elements Ne and the total number of nodes Nn are expressed as:





The results of this solution are the perforated fin temperature distribution along its length direction (x coordinate). Once the temperature distribution along the perforated fin length is obtained, the heat dissipation rate from the perforated fin ( Qpf ) can be computed by one of the following three expressions:
1- The expression of heat dissipation that depends on the integration over all the perforated fin surfaces which can be converted into summation over all finite elements as shown here:
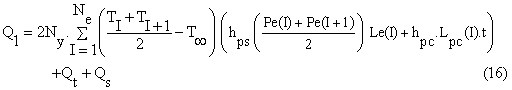
Where Qt and Qs are the heat dissipation from the tip and the two sides of the perforated fin, and can be calculated by the following expressions:
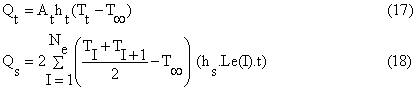
2- The expression of heat dissipation that depends on Fourier's Law which is applied at x = 0 as follows:
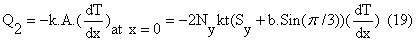
The first derivative of the temperature distribution at (x = 0) can be approximated by using the two temperatures of the two nodes of the first finite element of the fin as shown in the following expression:
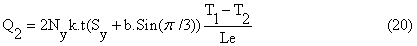
3- The expression of heat dissipation that depends on the first equation of the algebraic equation system which can be expressed as [15]:
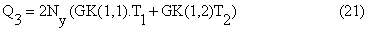
Where GK(1, 1) and GK(1, 2) are the first and second constants of the first algebraic equation in the finite element solution (In the Solution Matrix). The theoretical maximum heat dissipation of the fin is obtained when the temperature of the whole fin body equals the fin base temperature and it can be computed by the following expression:
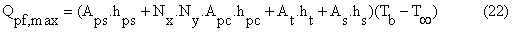
The fin efficiency is defined as the ratio of the heat transfer from the fin in its actual temperature distribution to its maximum heat transfer. Consequently, the fin efficiency is expressed as

In order to compare performance of the perforated fin with that of the solid (non-perforated) one of the same dimensions, the following equations of the solid fin consider convection heat transfer from its tip as described in [1] are used.
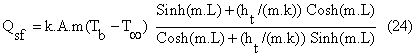
where m is defined as

Where Qsf is the heat dissipation rate of the solid fin [1]. The ratio of the heat dissipation of the perforated fin to that of the solid one (RQF) is introduced and given by:

This ratio indicates the heat dissipation improvements or the enhancement (augmentation) ratio of the perforated fin in according to its solid one counterpart.
It is believed that comparing the perforated fin with its solid counterpart is the best means to evaluate the difference in heat transfer brought about by introducing the fin perforations. In the following analysis, verification, and discussion, and where there is a comparison between the two fins, it is assumed that both fins have the same dimensions (L = 50 mm, W = 200 mm), same thermal conductivity, same heat transfer coefficient for all surfaces of the perforated and solid fins , and same base temperature  and (Tb 100 °C) = ambient temperature (T∞ = 20 °C) .The longitudinal and lateral perforation spacing are (Sx = Sy =1 mm). The other values are mentioned in their suitable places.
and (Tb 100 °C) = ambient temperature (T∞ = 20 °C) .The longitudinal and lateral perforation spacing are (Sx = Sy =1 mm). The other values are mentioned in their suitable places.
The temperature distribution along the fin length has an important effect on the fin's performance. Higher fin temperatures can be obtained as the fin's thermal conduction resistance is decreased. The temperature distribution of the perforated fin ( Tpf ) along the x-coordinate is plotted in Figure 4. From this Figure it is obvious that the temperature distributions show non uniform curves caused by perforations which lead to varying area of cross sections along the fin's length and then lead to varying thermal resistance in the fin along the fin length. The effect of variation of cross sectional area of the perforated fin on thermal resistance decreases as the thermal conductivity increases so the curves become more uniform. To compare the temperature distribution of the perforated fin with that of the solid one, the temperature difference distribution of the solid fin and the perforated fin ( Tsf -Tpf ) plotted in Figure 5. As shown in this Figure it is obvious that the temperatures along the solid fin are higher than those of the perforated one in all cases. This is because the thermal conduction resistance of the perforated fin is always higher than that of the corresponding non-perforated one. As the thermal conductivity increases the difference ( Tsf -Tpf ) decreases and it diminishes for very high thermal conductivities. That is, because as thermal conductivity approaches very high values, then the fin (solid or perforated) becomes almost isothermal with the base temperature (Tb). Figures 4 and 5 show that the temperature difference (temperature drop) between the fin base and its tip increases as the hexagonal perforation dimension (b) is increased. This is because the thermal resistance of the perforated fin increases as (b) is increased. Consequently, from only a temperature distribution viewpoint, it would be recommended to use a perforation with dimensions as small as possible. Also it can be deduced from temperature distribution that fin temperatures increase as the fin thickness is increased. This is readily explained by the fact that the thermal resistance of the perforated fin decreases as the fin thickness is increased. Therefore, from the temperature distribution viewpoint, it is preferable to use as large as possible fin thickness. The temperature and temperature difference distributions shown in Figures 4 and 5 indicate acceptable results as they are compared with those of the solid fin.
The heat dissipation rates (Q1, Q2, Q3 and Qpf,max ) of the perforated fin are plotted in terms of fin thermal conductivity with various hexagonal perforation dimension (b) and fin thickness as shown in Figure 6. The results show that Q1 differs from the values of Q2, Q3. The value of Q1 seems more acceptable because it doesn't exceed the maximum value (Qpf,max ). The values of Q2 and Q3 seem unacceptable because they fluctuate around and exceed the maximum value (Qpf,max ). The reason for wrong values of Q2 and Q3 is that these values as they are computed by equations (15, 16) in which the calculations depend on the temperatures ( T1and T2) at the two sides of the first finite element. This means that any error in ( T1and T2 ) will significantly appear on the values of Q2, Q3. The value Q1 depends on all temperaturesT1, T2, T3, ………., Tn of the finite elements. This means that the errors in the finite element temperatures along the fin length will diminish each others.
To check the stability and convergence of the perforated fin heat dissipations (Q1, Q2, Q3) according to the finite element number in the discretization mesh, they are plotted as a function of ( Nf ) in Figure 7, ( Nt ) in Figure 8, ( Nh ) in Figure 9. Again Q1 gives good stability and convergence, while Q2 and Q3 fluctuate irregularly below or around the (Qpf,max ). From the previous results the perforated fin's heat dissipation computed according to the integration overall the fin heat transfer surface Q1 is more accurate and acceptable. So it will be adapted in the following calculation.
For more verification of Q1, the difference (Qpf,max - Q1) as a function of fin thermal conductivity for various fin thicknesses and perforation dimensions is plotted in Figure 8. The theoretical knowledge of the fin analysis implies a positive difference of ( Qpf,max - Q1) and it converges to zero as the fin thermal conductivity approaches very high values. The results in Figure 8 are consistent with the theoretical knowledge mentioned above. To compare the perforated fin heat dissipation rate with that of the solid one, RQF is plotted as a function of perforation dimension as shown in Figure 9. It is theoretically expected that RQF should converge to (RQF = 1) as the perforation dimension approaches very small values. This situation is easily observed in Figure 9. From Figure 9 it can be deduced that the perforations for certain dimensions lead to heat transfer enhancement. This means that the use of perforation with certain dimensions leads to heat transfer enhancement, while the other values lead to heat transfer retardation.
The perforated fin efficiency according to the value of (Q1) is plotted in Figures 10-12. The efficiency has uniform curves with very small wiggles that converge to 100% as the fin's thermal conductivity approaches very high values. This result seems correct and acceptable.
1- The one-dimensional heat transfer solution of the perforated fin leads to acceptable results as the Biot Number in lateral and longitudinal directions less than 0.01.
2- The geometric modification made by perforation improves the performance of the fin for certain perforation dimensions.
3- The effect of thermal conduction resistance of the fin due to perforation can be decreased by increasing the fin thermal conductivity.
A: cross sectional area of the solid fin [m2]
Ac: cross sectional area of the longitudinal hexagonal perforation [m2]
Ae: cross sectional area of the finite element [m2]
Apc: area of the inner surface of the perforation [m2]
Aps.: area of the perforated surface of the fin [m2]
b: longitudinal hexagonal perforation dimension [m]
h: heat transfer coefficient [W/m2.° C]
hpc : heat transfer coefficient of the inner surface of the perforation [W/m2.° C]
hpc: heat transfer coefficient of the perforated surface of the fin [W/m2.° C]
hs: heat transfer coefficient of surface of the two sides of the fin [W/m2.° C]
ht : heat transfer coefficient of the fin tip [W/m2.° C]
k: thermal conductivity of fin material [W/m.° C]
L: fin length [m]
l: vector unit [m]
Le: finite element length [m]
N: number of perforations or finite elements or nodes
P: fin perimeter [m]
Pe: finite element perimeter [m]
Q: fin heat dissipation rate [W]
RQF: ratio of heat dissipation rate of perforated fin to that of non-perforated (solid) one
S: perforation spacing [m]
t: fin thickness [m]
Ve: finite element volume [m3]
W: fin width [m]
Subscripts and superscripts
b: fin base
e: finite element
f: finite element belonging to the regions type A and E
h: finite element belonging to the regions type C
max: maximum
pf: perforated fin
pc: inner surface of the perforation (lining surface of the perforation)
ps: perforated surface which is the remaining solid portion of the perforated fin
s: solid surfaces of the fin sides
sf: solid (non-perforated) fin
t: fin tip or finite element belonging to the regions type B and D
x: in or along the direction of x-axis
y : in or along the direction of y-axis
z: in or along the direction of z-axis