ISSN ONLINE(2320-9801) PRINT (2320-9798)
ISSN ONLINE(2320-9801) PRINT (2320-9798)
J. Shankar Babu1, Y. Ramya Sree2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering
Anomaly or outlier detection plays an important part in detecting intrusions in real world applications such as credit card frauds, customer behavior changes, defects in manufactured goods or devices etc., and to find out the deviated data instances. In this paper, to overcome the problems in anomaly detection we propose an algorithm of online oversampling principal component analysis osPCA. By using online updating technique, we detect the existence of anomalies in large scale data. Our approach is efficient and more interested in large scale or online problems .We can extract the principal direction of data by oversampling the target instance. Since the anomaly of the target instance is determined according to the difference of resultant principal eigenvector, the osPCA need not to perform eigen analysis. Our proposed construction is more special for online applications. When compared with other anomaly detection algorithms and PCA methods, our tentative outcomes confirm the achievability of our anticipated method is both efficient and accurate.
INTRODUCTION |
| As we know that anomalies or outliers are deviated small data instances in continuous observation of large scale online data. The method that is used to detect those anomalies is called anomaly detection or outlier detection. Basically these anomalies are found in real time applications such as credit card frauds, customer behavior changes, defects in manufactured goods or devices etc.,. Since only small amount of data is known in the above real world applications, it made an interesting challenge to researchers to find anomalies in unseen data. The presence of abnormal or deviated data in large scale may affect the solution model and its properties such as delivery and major instructions of data. Since anomaly detection needs to detect anomalies in unseen data i.e., unsupervised data machine learning is essential. |
| Adding and removing of outliers or abnormal data instances may lead to change in the final resulting data. So ‘Leave one out’ strategy is used to calculate the principal direction of the data set not including the presence of target instance. The difference in resultant principal direction will determine the presence of anomalies or outlierness. The accurate target instance is identified with the help of the difference between the eigen vectors. One can identify the outlier data by ranking the variations score of all the data points .This frame work is known as decremental principal component analysis (dPCA).This dPCA is efficient in the medium scale data instances where as in large scale data their differences in principal directions are not considerable. To overcome this difficulty, we proceed to the oversampling strategy which duplicates the target instance and osPCA is performed on oversampled datasets. Since the osPCA is performed on duplicates the effect of anomaly is reduced and its detection becomes easier. |
| Though we combined the LOO outlier detection method and oversampling technique, for each target instance everyone need to generate the covariance matrix which increases the computational weight. This feature in osPCA is not suitable for our real world large scale data or online applications. If we consider the power method to osPCA which gives reduced PCA solutions, but it needs lot of storage memory to store the covariance matrices which cannot be extensive to our online applications. For those reasons we propose an Online updating Technique to osPCA. Our proposed approach will permit us to calculate the reduced eigen vectors efficiently exclusive of eigen analysis and there is no need to store the covariance matrix. When compared with previous PCA methods and other outlier detection algorithms our proposed online updating osPCA will give good results irrespective of their computational costs and memory storage which is very suitable for our online streaming applications. |
ONLINE UPDATING OVER-SAMPLING PCA TECHNIQUE FOR OUTLIER DETECTION |
| Practically, the presence of single outlier in large dataset may not affect the difference in principal directions .As discussed prior, Adding and removing of single outlier or abnormal data instance does not affect the resulting principal direction of the data If we consider normal PCA technique in a p-dimensional space, we need to perform n PCA analysis for a dataset with n data instances which computationally not possible. For detailed derivations of osPCA, power method osPCA,online updating method osPCA refer to[3]. |
| To overcome these issues, we proposed over sampling PCA combined with an online updating technique. The target instances are duplicated multiple times and intensify the affect of outlier somewhat than that of normal data. Determination of outliers in all target instances without giving up the computational costs and memory requirements is the only aim of our proposed online updating osPCA.In particular situation like ,the target instance itself is an outlier than our approach is to oversamplize its affect on the principal eigenvector. With this, instead of manipulative numerous eigenvectors cautiously, we can make attention towards the rough calculation and extraction of dominant principal directions in online trend. |
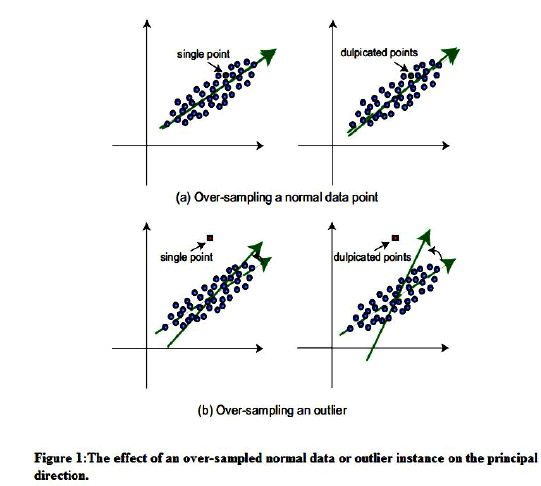 |
| We observe insignificant changes in the principal directions and representation of the data when normal data is considered as target instance to over samplize as shown in figure 1(a).It is significant that our osPCA determines the anomalies in the presented data and efficient in handling the outlier detection problems in online streaming data. |
| We also proposed an online updating osPCA algorithm to calculate the dominant eigenvector while over-sampling a target instance. Now we discuss about our proposed algorithm in detail. |
 |
| The detailed derivation of the u is explained in reference [3]. |
| Compared with dPCA, power method osPCA, our online updating osPCA is effective and good at its job. Online osPCA makes possible to detect outliers in real world applications which consists of large scale datasets. In our proposed approach we need not to store all the covariance vectors in the whole updating procedure, since the PCA is calculated in offline. |
| The simulated code in algorithm 1 resembles the online osPCA with online updating technique, in which we need to calculate x proj and y .once it is calculated the cosine resemblance is used to get the variation b/w the present and original devoid of oversampling. Then u is calculated to reduce the computational cost. |
| The table 1 shows the comparison between the power method osPCA and our anticipated online osPCA in accordance with computation complexity and memory requirements. |
 |
SYSTEM ARCHITECTURE OF ONLINE UPDATING OVER-SAMPLING PCA FOR OUTLIER DETECTION |
| In our real world applications to do filtration of spam mail we normally design a initial classifier by working out the usual data. |
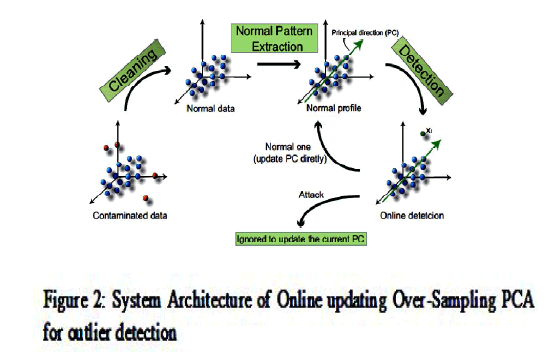 |
| The usual and anomalous data received is updated by the classifier. But in real world application even though the usual data is collected it may consists some noise and wrong labeling of data. In order to succeed with our approach one cannot discard these deviated instances online form the usual data. So, we anticipated system architecture of online updating osPCA for outlier detection. |
| It consists of three phases: Data cleaning, Data clustering and Online Outlier detection. |
Data cleaning: |
| In the data cleaning phase, prior to the outlier detection we filter all the deviated or abnormal data instances with osPCA in offline mode. The percentage of working out of usual data must be determined by us. In our approach we assumed 5percent to ignore from the usual data, after that we will get a negligible gain of anomaly (st) the rest of usual data as threshold for outlier detection. |
Data clustering: |
| In this phase we provide provable security to the usual or normal data, they are formed as different clusters using clustering method. Now, the clusters are passed as input data instances for outlier detection. |
Online Outlier detection: |
| The threshold value calculated in first phase is used to detect the outliers in each input cluster. If the gain of anomaly st is above the threshold then the input usual data is an outlier, if not it is considered as usual data instance and updated to our osPCA consequently. The principal direction of the input data instance cluster is used to detect the inward target instance. In the entire approach we need to carry the p-dimensional eigenvector so that the memory requirement is O(p).The proposed osPCA with online updating technique is used to determine the anomaly of input data instances by evaluating the updated Principal direction(PC). |
| The experimental results of our approach are shown in Table 1. Here outlier detection is done on some KDD intrusion detection data instances .The TP rate and FP Rate in the table are true and false positive rates respectively. |
 |
CONCLUSION |
| The work proposed in our paper is an online osPCA to find the anomalies or deviated instances in continuous observation in large scale online data. With LOO strategy our proposed over-sampling PCA identifies efficiently the unusual or anomalous data in online without calculating the eigenvector. When compared with many anomaly detection methods, our method is well efficient and has less computational cost and memory requirements. The results obtained from our approach are very acceptable. Our future work may include the online osPCA in online high dimensional data. Unlike our osPCA , there it needs to calculate the eigen vectors of multiple vectors since it is high dimensional data. |
References |
|