ISSN: 2319-9873
ISSN: 2319-9873
Department of Mechanical Engineering, Faculty of Engineering, University of Guilan, Iran
*For Correspondence
Received Date: 27/10/2016 Accepted Date: 23/11/2016 Published Date: 29/11/2016
Visit for more related articles at Research & Reviews: Journal of Engineering and Technology
Reducing energy consumption is the main purpose of design. Naturally, energy loss in each system can compromise the future of a system. This has drawn attention of researchers all around the world. Contentious structures the same as an engineering structure such as beam, plate, and shell are widely used in various industries. Much of industrial systems include these structures. However, the most important point in designing such structures is to avoid failure, reduce maintenance cost, and increase life of the structure. These points directly and indirectly can describe energy consumption and necessarily cannot meet the objectives of the design and not reach an optimal output and product. Vibration of any continuous system can have poor consequences on performance and can weaken the design of a system. Therefore, the effort to reduce vibration and control the mechanical phenomenon has a significant impact on reduced energy waste of a continuous structure (kinematic energy- potential energy). This paper sought to report scientific and research activities from 1980 to 2013 on vibration suppression of continuous systems focusing on optimal placement approach on the structure and installing piezoelectric S/A and smart model built by control approaches in order to attenuate and control unwanted vibrations of the system against external stimulations and disturbance.
Optimal placement, Vibration control, Piezoelectric sensor, Actuator, Structures, Energy, Controllability, Designs
The optimal placement of sensors and actuators does not exclusively belong to piezoelectric, but in this report, literature review is focused on the placement of piezoelectric on every kind of continuous structure which is discussed and investigated by many researches and if necessary, every picture related to each research is displayed.
Year 1980
Longman, et al. used a new method called controllability degree for the placement of sensors and actuators on air structures. The concept of controllability degree is for the standard maneuverability of air constructions which relies on the system's nature and structure. They proposed numerical methods to produce the optimal placement of sensors and actuators. They described that the controllability degree of a system will not change due to conversion of variables to other variables. Also controllability degree is time dependent [1].
Year 1981
Arbel used Oscillatory System measuring method in her article for the placement of actuator and sensor. Oscillatory system method is a method in which a linear description of flexible air structures is provided. The logic of this approach is based on the minimization of wasted energy which is closely associated with system's controllability and results in the optimal placement of actuator on the structure and increases the controllability degree of system [2].
Year 1992
Liu, et al. tried to find a suitable and optimal place for locating sensor and actuator on a flexible structure based on controllability and observability criteria. Their studied structure was beam and plate with two-headed simply supports. During their research, they found out that optimal placement for actuator and sensor results in the balance of systems two up and down [3].
Year 1994
Dhingra, et al. analyzed the optimal placement of sensor and actuator on aeronautics structure "ACOSS-Four". Their optimization method was a combination two optimization methods including Synergistic Blend of Artificial Genetic Search (SBAG) and Gradient- Based Search (GBS) by which they tied to find out the suitable number and place of sensors and actuators (Figure 1). They followed two important objectives in this research [4]:
Figure 1: Aeronautics structure ACROSS-four [4].
1) The minimization of structure's weight through Eigen-values and damping coefficient of structure.
2) Using a control approach called LGR for controlling the structure and reaching vibration suppression.
Year 1995
Furugya proposed a process for reaching an optimal coordinate in order to find the best place for locating the piezoelectric actuator (Figure 2). Finally, by using the best performance criterion for piezoelectric actuator and Genetic Algorithm (GA) for determining the best optimal place for actuator, they proposed 8 optimal places [5].
Figure 2: Structural study at NASA [5].
Year 1996
Lee, et al. tried to optimally locate the piezoelectric actuator for a cantilever plate. During their investigation, they found out that the placement of piezoelectric actuator in an unsuitable place for controlling the vibration of a plate decreases the controllability of system and develops the spillover phenomenon (Figure 3). They concluded that by increasing the specific number of piezoelectric actuators and fining the best place for controlling the system, many vibration modes can be damped in that unit [6].
Figure 3: Cantilever plate with geometric characteristics [6].
Year 1999
Sadri, et al. investigated the optimal placement of piezoelectric piece on an isotropic plate with the boundary condition of Simply-Support. Their optimization method is for plate's dynamics based on Rayleigh-Ritz method and two criteria was simultaneously considered for optimization through genetic algorithm in order to find the optimal place and locating the piezoelectric on it. These two criteria include [7] (Figures 4 and 5) :
Figure 4: Optimal placement selection in plate [7].
Figure 5: Frequency response with 2 approaches control [7].
1. Modal controllability
2. Controllability gramian
Mirza, et al. investigated the optimal placement on Pined-Pined beam and L-shaped shell in their article. They proposed a new criterion for finding the best place in order to avoid the vibration in their systems. Their criterion was presented as objective function called gramian sensitive to disturbance. They minimized this criterion by the placement of piezoelectric actuator and locating it on the structure [8].
Jae-Hung H, et al. worked on a composite cantilever plate by using Layer wise Displacement Theory and finite element method in order to search a place for the placement of piezoelectric sensor and actuator for vibration suppression of this structure, as their objectives included system's controllability, observability and spillover (Figure 6). By using Positive Position Feedback controller (PPF) and optimization method for finding the optimal place using genetic algorithm, they controlled three first vibration modes of composite plate [9].
Figure 6: Modeling electromechanical cantilever composite plate [9].
Year 2000
Bruch, et al. conducted a research on three optimal objectives. These included the location of piezoelectric as sensor and actuator, geometry of piezoelectric and the voltage applied to the piezo actuator (Figure 7). They concluded in this research that by comprehending the geometry of piezoelectric patches, the output force from it and the piezoelectricpotential in the production of applied load for eliminating the vibration can be determined [10].
Figure 7: Simply-supported beam with sensor and actuator PZT patch [10].
Wang, et al. conducted a research for optimizing the place and size of piezoelectric patches in order to control the beam and its vibration suppression by using the controllability index of system on the beam structure. They find the best size or volume (length-width-height) of piezoelectric and the best place (for structure damping) by using the amount of sensitivity, controllability index and mesh design of whole beam. Because the controllability index of system was dependent on the size of piezo actuator and its location through modal analyze [11].
Halim D, et al. investigated the optimal placement of piezoelectric by using controllability and observability index of system on a thin clamped-clamped plate so that by using position controllability, ordering of the place of actuator and sensor and piezoelectric pieces can easily happen (Figure 8). They implemented the controllability index of system based on H00 soft concept. Each coordinate in plate showing more controllability in vibration mode is a suitable place for locating the piezoelectric actuator for structure damping [12].
Figure 8: Experimental model [12].
Aldraihem, et al. investigated the placement of one or two piezoelectric actuator pieces considering the size and weight of the piece. For Euler-Bernoulli beam model with 6 different boundary conditions be close to the real model, the weight of piezoelectric actuator patches should have an effect on strain energy of the beam; since it considerably affects the strain energy and stiffness of the beam (Figure 9). They believed that piezoelectric patches should be located on a coordinate of the beam which has the highest strain energy and by locating the piezo on this specific coordinate, damping of the beam can be obtained [13].
Figure 9: Beam under investigation in this study with different boundary conditions with piezoelectric sensor and actuator [13].
Bin, et al. used Maximum Modal Force method to control the plate with specific boundary conditions, so that the discrete distribution of piezoelectric pieces on plate should happen on places with maximum modal force in order to damp and control the structure. They had these following objectives during the optimal placement of piezoelectric pieces on plate.
1. System stability
2. Controllability
3. The efficiency of controlling system
In fact they considered coordinates for piezo actuator which has the highest strain or displacement (Figure 10). In fact the highest strain is characterized according to the highest model force in that mode [14].
Figure 10: The geometry of the piezoelectric patches for optimum positioning on the plate [14].
Year 2001
Abdullah, et al. conducted the optimal placement of piezoelectric sensor and actuator on civil engineering structures by using genetic algorithm. Their proposed method is simultaneously locating piezoelectric sensor and actuator on the structure, as it was previously presented for the placement of sensor and actuator consequently and sequentially in optimal places [15].
Year 2002
Oude Nijhuis, et al. conducted the vibration suppression of a cantilever plate by using piezoelectric as sensor and actuator. Their objective was to reduce the released sound from the plate due to the vibrational behavior of the structure. They tried to control the vibration of structure by the placement of piezoelectric through genetic algorithm [16].
Yan, et al. found the optimal place for locating the piezoelectric sensor and actuator by using genetic algorithm and in addition to the optimal place; they optimized the number of sensors and actuators used in this intelligent system by using the controlling force and eigenvalues matrix of piezoelectric energy [17] (Figures 11-15).
Figure 11: Optimal placement in truss models [17].
Figure 12: Vibration suppression in model a [17].
Figure 13: Vibration suppression in model b [17].
Figure 14: Vibration suppression in model c [17].
Figure 15: Vibration suppression in model d [17].
Year 2003
Quek, et al. investigated the vibration suppression of multilayer composite plate as cantilever and four sides clamped and find the best place for locating the piezoelectric sensor and actuator. By using finite element, they completed a numerical modeling. By using two perspectives, one of them based on controllability of mode and the other based on controllability of intelligent system, they extracted the objective function. Finally, they used Direct Pattern Search method (DPS) to optimize these objective functions and presented their results [18].
Year 2004
Liu, et al. optimized the location of the piezoelectric sensor and actuator by using H2 controller and genetic algorithm (Figure 16). During the simulation of their model, they used H2 soft performance index as a good performance index in order to control the vibration of a plate with two simply supports [19].
Figure 16: Electromechanical models with optimal location using a piezoelectric [19].
Guo, et al. conducted the optimal placement of piezoelectric sensor and actuator on a truss structure by using genetic algorithm. Their objective was to keep this structure safe against external stimuli it means that their objective function was considered according to the fault detection in system. But they implemented several reforms and suggestions in genetic algorithm: firstly, they used Penalty Function Method (Figure 17). Second, they used Force Mutation Method to increase the convergence rate of algorithm to the most efficient possible locations for placement of piezoelectric [20].
Figure 17: Truss structure in research [20].
Da Rocha, et al. conducted the optimal placement of piezoelectric on a cantilever plate as sensor and actuator by using
H00 soft concept. Modeling of structure was done by using finite element with ANSYS and MATLAB software. By using 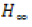 and
Linear Matrix Inequalities (LMI) method, they calculated the location of sensor and actuator on structure which finally resulted in
vibration suppression due to the optimal placement of piezoelectric [21].
and
Linear Matrix Inequalities (LMI) method, they calculated the location of sensor and actuator on structure which finally resulted in
vibration suppression due to the optimal placement of piezoelectric [21].
Santos SLD, et al. generally conducted the optimal placement of piezoelectric sensor and actuator on a truss structure called Kagome Truss and their optimization algorithm included annealing and genetic algorithms and had good results from this research [22] (Figure 18).
Figure 18: Kagome truss structure [22].
Brasseur, et al. conducted the optimal placement of piezoelectric on an acoustic structure called Wooden Shutter Box by using controllability gramian index. The modeling method of this structure included finite element. The objective of this experimental and theoretical research was reaching desirable coordinates for the placement of piezoelectric in order to absorb sound in the room's environment [23].
Ning in an article investigated and optimized the place and number of piezoelectric on a cantilever plate as sensor and actuator to control the undesirable vibrations in the structure (Figures 19-26). In order to search the working environment of cantilever plate, genetic algorithm was used to find the best location of piezoelectric sensor and actuator [24].
Figure 19: Cantilever plate with actuator PZT patch locating [24].
Figure 20: Vibration responses plate for optimal locations in different inputs [24].
Figure 21: Optimal location in active vibration control plate for different inputs [24].
Figure 22: Displacement responses plate for 6 models [24].
Figure 23: Vibration control plate with different number PZT actuator for case study a [24].
Figure 24: Vibration control plate with different number PZT actuator for case study b [24].
Figure 25: Vibration control plate with different number PZT actuator for case study c [24].
Figure 26: Vibration control plate with different number PZT actuator for case study d [24].
Year 2005
Oliveira, et al. conducted the optimal placement of piezoelectric sensor and actuator patches to form an intelligent structure on a simply support beam by using classic optimization. They extracted the critical coordinates by deriving figure function and put it equal to zero and by the placement of piezoelectric on these specific coordinates, they controlled its vibration. For controlling the system, they used Singular Value Decomposition (SVD) method as the objective function [25].
Year 2006
Wang, et al. optimized the location of piezoelectric sensor and actuator on a cantilever plate. In this research, they considered piezoelectric sensor and actuator as isotropic and anisotropic so that can damp torsional vibrations of a composite plate. Modeling of composite plate was used through finite element which was based on the first order shear method and genetic algorithm was used to conduct the optimization process [26].
Lottin J, et al. in a descriptive article studied the optimal placement piezoelectric sensor and actuator on a structure (Figure 27). During four sections, they described placement methods, type of actuator and sensor in terms of efficiency and performance, type of structure, methods of assembling piezoelectric on a structure, methods of controlling system and place optimization criteria [27].
Figure 27: Electromechanical cantilever beam model the laboratory [27].
Swann, et al. by exclusive placement of piezoelectric sensor on a composite plate with boundary conditions of cantilever and four sides clamped, tried to find delamination phenomenon in structure due to vibration. Modeling structure was done by using finite element based on Refined Layer-wise Theory (RLWT). For conducting the optimization process for the place and number of sensors, genetic algorithm and Monte-Carlo Method was used to produce the initial population (Figure 28). Their objective was a troubleshooting method due to the optimal location of piezoelectric sensor for detection of composite delamination because of receiving voltage signals and comparing it to the non-delamination situation [28].
Figure 28: 4 Models to find the optimal location for a clamped-free plate [28].
Belloli, et al. analyzed the placement of piezoelectric ceramic pieces to neutralize the vibrations in rear wings of a race car. Optimization was done by using CATIA V5, ANSYS 9.0 and DynOPS software and it was completely designed and analyzed (Figure 29). The objective of optimization in this research was finding the best size, place and direction for the placement of piezoelectric and interesting results were extracted [29].
Figure 29: Wings of a race car [29].
Zhi-Cheng in their article studied cantilever plate model analytically and by using controllability degree and observability index of system, they optimized the placement of piezoelectric for vibration depression of structure. In this article, they tried to control the vibration of plate by combining two control methods including PPF and PDC (Proportional Derivative Control) (Figure 30). The type of studied vibration was torsional and flexural vibration. By making the torsional and flexural coupling relations independent through Bandwidth Butterworth Filter (BBF) method, they analyzed the vibration of system and applied controlling rules on them [30].
Figure 30: An experimental model of a cantilever plate in laboratory [30].
Year 2008
Roy, et al. conducted a research on the optimal placement of piezoelectric patches by using genetic optimization algorithm and quadratic optimal control or LQR method. Their studied structures included Spherical composite panel, a cantilever composite beam and a composite plate. One of the innovations in this study was using multilayered piezoelectric composite pieces as sensor and actuator. By incorporating LRQ method and algorithm, it can be said that in LQR method, 3 coefficients in R and Q fixed matrixes are defined and by using genetic algorithm, the most optimized answer for these three coefficients is obtained (Figures 31-34). Finally, by the placement of these coefficients in energy relationship, the best places for actuator and sensor can be suggested [31].
Figure 31: Find optimal location by the mesh and piezoelectric sensors and actuators on plate [31].
Figure 32: Active vibration control plate with GA-LQR approach [31].
Figure 33: Find optimal location by the mesh and piezoelectric sensors and actuators on panel [31].
Figure 34: Active vibration control panel with GA-LQR approach [31].
Year 2010
Safizade, et al. studied the optimal place for a plate with all edges clumped by using controllability gramian performance index and genetic algorithm. Structural equations of plate were extracted analytically and were incorporated with analytical equations of piezoelectric actuator and the equation of an intelligent structure was obtained. Then by using a controlling method, the optimal placement of their system was conducted. In this method, the main responsibility is system's controllability and expressing an optimum control input so that by applying forces on this optimal place of structure, system, can be damped [32].
Yang J, et al. in two researchers studied the optimal placement of piezoelectric sensor and actuator on a plate. Their theory was that in order to increase the controlling performance of system or in other words controlling the system by piezoelectric results in vibration suppression, piezoelectric actuator should affect a specific direction on plate. Now there are coordinates on the plate that show their potential effect by the placement of piezoelectric actuator and system is controlled more efficiently. They used two types of Simulated Annealing for the TSP (SATSP) algorithm and another algorithm called Hopfield-Tank for the TSP (HTTSP) to optimize the place of plate. The results of SATSP optimization algorithm were better than HTTSP (Figure 35). In this article, by using SATSP algorithm alongside Genetic Algorithm for TSP (GATSP) algorithm, better results from GATSP were provided compared to SATTSP [33,34].
Gupta, et al. in a practical and helpful research used 6 objective functions for optimizing the placement of piezoelectric as sensor and actuator on the structure of beam and plate. These functions include [35]:
1. The maximization of force or torque released from piezoelectric actuator
2. The maximization of deflection in a structure
3. The minimization of controlling effect or the maximization of wasted energy
4. The maximization of controllability degree
5. The maximization of observability degree
6. The minimization of spillover phenomenon
Year 2012
Trajkov, et al. analyzed the placement based on controllability and observability criteria. The optimization was conducted based on H2 and H00 soft and controllability and observability gramian function which is dependent on vibrational modes. The structure model was designed using finite element and after the reduction of order process, optimization operations were done on the reduced model and the optimal place was suggested for the plate and cantilever beam [36].
Bachman F, et al. conducted a research on optimal placement of two piezoelectric pieces on a turbo machinery blade which is a carbon / epoxy composite and by using the criterion of increasing potential energy for piezoelectric and structure and increasing electromechanical coupling damping coefficient (Figure 36), they tried to increase the energy saved in piezoelectric in the best place of a composite blade [37].
Figure 36: Turbomachinery blades [37].
Zhang, et al. analyzed the vibration suppression of a cantilever beam by finding the best place in that beam for the placement of piezoelectric actuator and sensor in order to from an intelligent system for automatically controlling of the vibration and reaching a logical stability (Figure 37). For system's steering, they used Linear Quadratic Gauss (LQC) controller as an optimal controller method and analyzed 4 vibration modes of beam [38].
Figure 37: Displacement response in optimal location [38].
Molter, et al. studied the optimal placement of piezoelectric on a flexible Manipulator as a cantilever beam with its mass concentrated on top of the beam. They studied and controlled the beam based on Euler-Bernoulli theory analytically and numerically (Figure 38). In addition to optimal placement, they optimized the size of piezoelectric sensor and actuator in this model and their controlling method was done by using Lyapunov function [39].
Figure 38: Flexible manipulator as a cantilever beam with PZT patch [39].
Nowak, et al. proposed a method for calculating the optimal place of piezoelectric sensor and actuator. Thin beam, thin plate and thin panel were tested as structures with different boundary conditions under acoustic vibration. The dynamic analysis of structure was conducted analytically [40].
Rosi G, et al. controlled the inactive released sound on an aluminum plate with non-standard boundary conditions and by optimal placement on it; they considered coordinates for locating piezoelectric pieces (Figures 39-41). Generally the objective was reaching the best efficiency of this plate in reducing the released sound from it [41].
Figure 39: Test model in laboratory [41].
Figure 40: Velocity control sound response in FRF approachh [41].
Figure 41: Pressure control sound response in FRF approach [41].
Daraji, et al. used an isotropic cantilever plate through finite element method in ANSYS software by using 2 elements; element Solid45 for 3D meshing and element Shell 63 for 2D meshing of plate. They also used element Solid45 for meshing piezoelectric sensor and actuator pieces and prepared the model for controlling and by using Linear Quadratic performance index (minimization) and genetic algorithm in MATLAB software, they were able to relate these two software simultaneously in order to accelerate the vibration suppression through the optimal placement of piezoelectric pieces and showed their results [42].
Hale JM studied their placement by 10 piezoelectric pieces as sensors and actuators on a cantilever plate. They used genetic algorithm for optimization of objective function. Modeling method was in accord with first order shear theory and was conducted numerically by finite element and Hamilton relationship. Their objective for optimal placement was reaching the damping of first 6 vibrational modes of plate which were implemented analytically by ANSYS software by using element Solid45 for 3D meshing and element Shell63 for 2D meshing of plate and compared their results with finite element method. Optimized objective function was modified by H2 soft in genetic algorithm to find the optimal place [43].
Nemanja, et al. tried to optimized the size and location of piezoelectric on a thin composite beam by modeling finite elements based on the third order shear deformation theory (Figures 42 and 43), using fuzzy logic combination and PSO optimization algorithm with the swarm of one objective particles [44].
Figure 42: Composite thin beam with PZT patchess [44].
Figure 43: Different models in vibration control modes [44].
a) Optimal size and placement PZT
b) Degree of controllability diagram
Year 2013
Sergio, et al. used piezoelectric pieces for the optimal location on a cantilever beam and a plate with simply support. Their optimization method was genetic binary algorithm and Linear Quadratic Gauss (LQG) method. In this study, their optimization objective function was designed based on Lyapunov function. During this research, they reached to this goal that optimal location in many first modes that are considered as energetic modes can control the system and cover other vibration modes (Figure 44). State variables, kinetic energy, strain energy and input voltage of actuator are considered and considerable results were provided [45].
Figure 44: Cantilever beam with geometric characteristics by using triangular element meshing [45].
Chhabra, et al. in their article optimally located 10 piezoelectric actuators on a square plate with simply support by using Modified Control Matrix and Singular Value Decomposition (MCSVD) method and genetic algorithm and finally for vibration control, they used LQR controlling rule in order to investigate the performance and efficiency of system and this way, they optimized and controlled first 6 vibration modes in square plate [46].
Botta, et al. suggested a new objective function for optimal locating of piezoelectric. Optimization of the objective function results in simultaneously damping of several vibration modes. Heir studied structure was a cantilever beam with using Euler- Bernoulli theory. Their modeling of beam was done in two ways; analytically and numerically and showed the conformity of these two methods. Also in another article, they obtained experimental results from optimal placement of piezoelectric as sensor and actuator on turbo machinery blades. They considered a turbo machinery blade as a cantilever beam and then analytically solved the equation of beam coupled with piezoelectric sensor and actuator and presented their theoretical and experimental results. Their objective was to reduce vibration and fatigue of the beam [47].
Araujo, et al. conducted the optimal placement of piezoelectric on a Sandwich plate with viscoelastic core and multi-layered procedure by using DMM optimization method. Because of this research, they were able to analyze the vibration suppression of sandwich plate by finding the best place and by analyzing 6 vibration modes. They found considerable results [48].
Wrona et al. in two different articles used local directional controllability theory to find the optimal place for piezoelectric sensor and actuator. Their studied structure was isotropic square plate with four sides clamped. They used Memetic algorithm to optimize the controllability index. Memetic algorithm has a proper performance due to faster convergence and better statistical solution [49,50].
What researches considered in different studies can be stated as:
• Finding an optimal place by a piezoelectric element or various elements with reducing of its size
• One objective or classis optimization for finding the optimal place of piezoelectric element
• Identification and investigation of effective criteria for finding the optimal place
• Disregarding the shear effect of beam (Euler-Bernoulli)
• Dividing the beam to finite elements
• The unimportant role of controller or choosing it with optimal locating of piezoelectric elements as sensor and actuator
• The analyses conducted on the vibration suppression of structure were focused on Impulse input