Keywords
|
| Blowfish, Optimized Blowfish, Encryption Time, Decryption Time, Throughput. |
INTRODUCTION
|
| Cryptography is the science that is widely used for network security [2]. Cryptography means to transfer sensitive information across insecure networks such as internet [3]-[5]. Key aspects of cryptography are confidentiality, integrity, authentication, and non repudiation [1] [2]. An original message is known as the plaintext, while the coded message is called the ciphertext. The process of converting from plaintext to ciphertext is called encryption; restoring the plaintext from the ciphertext is decryption [6]. |
| Cryptographic algorithm is classified into two categories: (i) Symmetric Key Cryptography where one key is used for both encryption and decryption. (ii) Asymmetric Key Cryptography where two different keys are used one for encryption and other for decryption [7]. Symmetric key cryptography is divided into two types on the basis of their operations [8]: (i) Stream Cipher: A stream cipher is one that encrypts a digital data stream one bit or one byte at a time. (ii) Block Cipher: A block cipher is one in which a block of plaintext is treated as a whole and used to produce a ciphertext block of equal length [6]. |
| Blowfish is a symmetric block cipher designed by Brute Schneier in December 1993. Blowfish is a replacement of DES or IDEA [14]. Blowfish algorithm is a symmetric block cipher with a 64-bit block size and variable key length from 42 bits to 448 bits [9] [10]. |
RELATED WORK
|
| Manikandan G, Rajendran P, Chakarapani K, Krishnan G and Sundarganesh G (2012) modified the Blowfish algorithm for enhancing data security. They designed a software tool for encrypting the file. A file is divided into a number of pieces depends upon the users specification and then the encryption algorithm is applied. To enhance the performance of the software they modified the F-function in Blowfish algorithm. The F-function consists of 4 S- boxes (S1, S2, S3 and S4). The F-function is defined as F(X)=(( S1+ S2 mod 232) XOR S3+ S4 mod 232. They modified this F-function into F(X) = ((S1 XOR S2 mod 232) + (S3 XOR S4 mod 232)). They experimentally proved that the execution time of modified Blowfish is 14% lesser than the original Blowfish algorithm [8]. |
| Monika Agrawal and Pradeep Mishra (2012) enhanced the security level of Blowfish algorithm and decrease the time for encryption and decryption. They generate the random number within the range 0 to 65535. Set the flag value to zero. Convert random number into 16 bit binary form and finds the positions that are holding 0 entries, change the flag value to one otherwise flag is zero. If the flag is 1 then the F-function will not work, it the flag is 0 then the Ffunction will work. In every round a new random number is generated and this as a result gives difference in the application of F function. They analysed that the encryption time and decryption time is reduced compare than original Blowfish algorithm [10]. |
| Israa Tahseen and Shatha Habeeb (2012) proposed a new approach to generate a random number using image. Read the picture by pixel, select the specific location randomly pick any two colors. Apply XOR between two selected colors then specify the length of the key. This key is used to encrypt or decrypt the plaintext. They apply this key generation method in to Blowfish algorithm. Finally they suggest that this type of key generation is suitable for short keys in symmetric system [11]. |
| Ratinder Kaur and V. K. Banga (2012) proposed a security of image using Blowfish algorithm. They divide the original image into a random number of blocks and then the blocks are transformed into new locations. For better transformation divide the blocks into a smaller number of blocks because fewer pixels keep their neighbours and difficult to predict neighbours pixels. For better performance divide the block into larger number then the correlation was reduced even further and the entropy was increased. After that transformation encrypt the block of images using Blowfish algorithm. Finally they analysed that combination of transformation and encryption provides better security for image [12]. |
| B.Geethavani, E.V.Prasad and R.Roopa (2013) proposed a new approach for secured the data, transfer in audio signals using discrete wavelet transform. They derived to new hybrid technique from the combination of cryptography and stegnography for transmitting the message in a highly secured manner. The plaintext is encrypted using Blowfish algorithm and the resulted cipher text is embedded into an audio file using discrete wavelet transform. Finally they suggest this method is efficient method for hiding text in audio files such that data can reach the destination in a safe manner without any modification [13]. |
| This paper is organized as follows: section III describes optimized Blowfish encryption algorithm and section IV provides the Pseudo code of Optimized Blowfish comparative analysis of original Blowfish and optimized Blowfish encryption algorithm based on execution time and throughput, and section V presents the conclusion and future enhancement. |
OPTIMIZED BLOWFISH ENCRYPTION ALGORITHM
|
| Optimized Blowfish is a 64 bit block cipher with a 448 bit key length. It is a Feistel network consisting of 16 rounds. The relative strength of the encryption algorithm is based on key length. Optimized Blowfish algorithm keeps two sub key arrays: P-array and two 32 bit S-boxes. This algorithm is divided into three main parts: sub keys generation, S-Box preparation and Encryption. |
| Description of optimized Blowfish Encryption Algorithm Sub key generation (P-array): Initialized the P-array with fixed string. It contains eighteen 32 bit sub key values. Separate the key string into eighteen 32 bit. The first P-array (P1) value is XORed with the first 32 bit key (K1), second P-array (P2) value is XORed with the second 32 bit key (K2), third P-array (P3) value is XORed with the third 32 bit key (K3) up to 18 rounds. That means each eighteen 32 bit P-array value is XORed with eighteen 32 bit key values. All zero string is encrypted using optimized Blowfish encryption algorithm. This process is executed in 18 rounds. After that the sub key values are stored in P-array. |
| S-Box preparation: Initialize the four S-boxes with fixed string. Each S-box consists of 256 entries. These S-box values are encrypted using Blowfish encryption algorithm. After that first and second S-box values are concatenated and third and fourth S-box values are combines together. Finally the four S-box values are reduced into two S-boxes. |
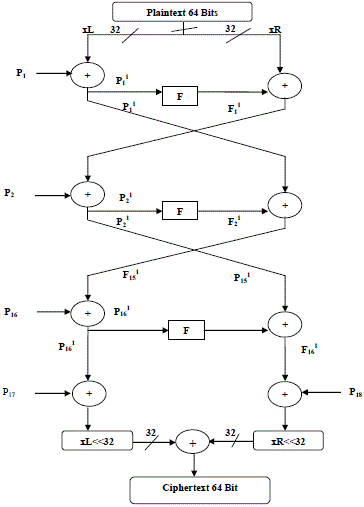
| Data Encryption: Data encryption consists of F function with 16 rounds. Each round consists of a key dependent permutation and a key-and-data dependent substitution. Each round every left half is affected by the right half as well as every subkey is affected by every key. The figure 1 shows the structure of Blowfish algorithm. This structure is same as optimized Blowfish algorithm. |
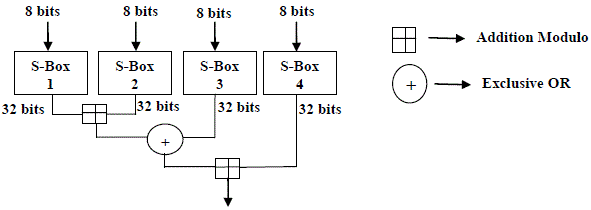
| Function F is not reversible, gives the best possible avalanche effect for a Feistel network. The original Ffunction consists of four S-boxes. The input of 32 bit is divided into four 8 bits. These four eight bits values are mixed using addition modulo and combined using XOR. The figure 2 illustrates the function F. |
Modified F function
|
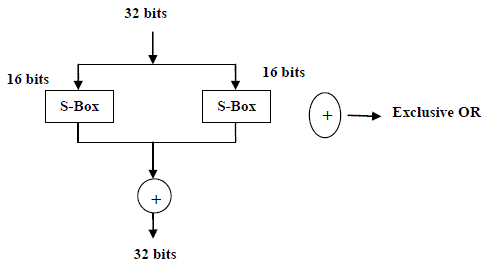
| The only change is S-boxes in the F-function. The Feistel structure of Blowfish algorithm is not changed but the structure of F-function is modified. The original Blowfish algorithm F-function has four S-boxes but the optimized Blowfish F-function has two S-boxes. The figure 3 illustrates the modified structure of F-function. |
| The working of Optimized Blowfish Illustrated as follows |
| 1. Initialized the P-array and four S-boxes, in order with a fixed string. |
| 2. Encrypt the key and P-array for prepare the sub keys. |
| 3. Encrypt the S-box values using F function with four S-boxes |
| 4. Divide the 64 bit input data into two 32-bit halves (left and right). The left half is denoted by XL and right half is denoted by XR. |
| 5. The 32 bit left half XL is XORed with the sub key P1 and assigned into the XL. The XL is fed into the F function. |
| 6. The F function consists of two S-boxes. F function splits the 32 bit of input into two 16 bit halves and each half is input to each S-boxes. |
| 6.1 The first 16 bit S-box (S1) and second 16 bit S-box (S2) are added. |
| 6.2 The 32 bit resulted bit is XORed. |
| 6.3 The optimized F function is as follows: Divide XR into two 16 bit halves: a, and b. |
| F(XL) = F(a, b) = (S1 ? S2) Here “?” is XOR. |
| 7. F(XL) is XORed with XR |
| 8. Interchange (Swap) the XL and XR values that means right half (XR) becomes new left half and left half (XL) become new right half (XR). |
| 9. After the 17th round left half and right half are not swapped but the XR is XORed with P17 and XL is XORed with P18 |
| 10. Finally XL and XR are recombined using exclusive OR. |
| 11. Decryption is same as encryption, but P0, P1,..., P17 are used in the reverse order. In case of original F-function which executes in sequential order and it requires two Addition operations and one XOR operations. But in the case of optimized F-function requires only one XOR operation. To reduce four S-boxes entries in to two S-boxes cannot affect the security. |
PSEUDO CODE
|
| A. Pseudo-code of F-Function with four S-Boxes (S0, S1, S2 and S3) |
| Step 1: Divide xL into four eight-bit quarters: a, b, c, and d |
| Step 2: F(xL)=((S0,a+S1,b mod 232)^S2,c)+S3,d mod 232. |
| B. The Pseudo-code of optimized F function with two S-boxes |
| Step 1: Divide xL into two sixteen-bit quarters: a, and b. |
| Step 2: F(xR)=(S0,a^ S1,b) |
| C. Pseudo-code of Encryption |
| Step 1: Divide the 64 bit input data into two 32-bit halves (left and right): xL and xR |
| Step 2: for i=0 to16 |
| xL is XORed with P[i]. |
| Find F(xL) |
| F(xL) is XORed with xR. |
| Interchange xL and xR. |
| Step 3: Interchange xL and xR. |
| Step 4 : xR is XORed with P[16]. |
| Step 5: xL is XORed with P[17]. |
| Step 6: Finally combine xL and xR. |
| D. Pseudo-code of Decryption |
| Step 1: Divide the 64 bit input data into two 32-bit halves (left and right): xL and xR |
| Step 2: for i=17 to1 |
| xL is XORed with P[i]. |
| Find F(xL) |
| F(xL) is XORed with xR. |
| Interchange xL and xR. |
| Step 3: Interchange xL and xR. |
| Step 4: xR is XORed with P[1]. |
| Step 5: xL is XORed with P[0]. |
| Step 6: Finally combine xL and xR. |
SIMULATION RESULTS
|
| A comparative analysis of original Blowfish and Optimized Blowfish is performed to provide some measurements on the encryption and decryption. The following parameters are used as the performance criteria, such as input size (in bytes), Encryption time, Decryption time and throughput. |
| These algorithms are implemented in Java jdk1.7 and developed using in Eclipse (4.2.0) integrated environment. Performance was measured on a Intel(R) Core(TM)2 DUO CPU T6600 @ 2.20 GHz processor with 3GB RAM running Windows 7 Home Basic 2009, Service Pack 1. |
| C. Performance Comparison on the basis of Execution time and Throughput |
| The comparison is conducted for the text or message only. Encryption time is one of the performance parameter, which is defined as the amount of time required for converting plaintext into ciphertext at the time of encryption. Decryption time is also one of the performance parameter, which is defined as the amount of time required for converting ciphertext into plaintext at the time of decryption. To improve the accuracy of the timing measurement, the program is executed in 10 times. The encryption time and decryption time is measured by milliseconds. The sum of encryption time and decryption time is considered as the execution time. |
| Execution time=Encryption time + Decryption Time. Table I shows the total execution time. |
| From the result identified that the average execution time of optimized Blowfish is 6.83 milliseconds and the original Blowfish is 7.03 milliseconds; comparison of these two average execution time, optimized Blowfish algorithm is less than original Blowfish algorithm. |
| D. Performance comparison on the basis of Throughput |
| The throughput of the execution scheme is calculated as the total encrypted plaintext size in bytes divided by the total execution time. Throughput indicates the speed of encryption. The throughput of the execution scheme is calculated using the following formula. |
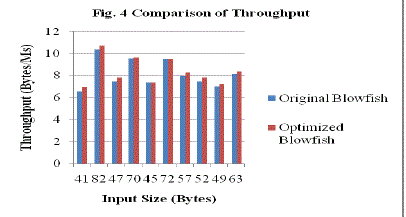
| Throughput=Total size of plaintext /Total execution time. Where plaintext size is measuring in bytes and total execution time is measuring in milliseconds. Comparison of throughput of these algorithms is shown in Figure 4. |
| The throughput of the execution scheme is calculated as the total encrypted plaintext size in bytes divided by the total execution time. Throughput indicates the speed of encryption. The above graph shows the result based on the throughput of the execution time with different input size. It shows that the throughput is high for optimized Blowfish when compared to original Blowfish algorithms. As the throughput value is increased, the execution time of encryption is decreased. |
CONCLUSION
|
| In this paper an optimized Blowfish has been developed. The longer key size is more secure but the encryption time and decryption speed is slow. In order to overcome this problem in Blowfish algorithm reducing of two S-boxes will increase the speed and provide the better security to data. The main advantage of optimized Blowfish is that the execution time is reduced to 0.2 milliseconds and the throughput is increased to 0.24bytes/milliseconds compare than original algorithms. In future, cryptanalysis of optimized Blowfish algorithm will be investigated and this algorithm is tested with other data type such as text file, audio and video. |
Tables at a glance
|
 |
| Table 1 |
|
Figures at a glance
|
 |
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
Figure 4 |
|
References
|
- Behrouz A. Forouzan, “Cryptography and Network Security”, Tata McGraw-Hill, 2nd edition, 2008.
- Anand Kumar M and Dr. S. Karthikeyan, "Investigating the Efficiency of Blowfish and Rejindael Algorithms", International Journal of Computer Network and Information Security, pp. 22-28, 2012.
- Obaida Mohammad Awad Al-Hazaimeh, "Design of a New Block Cipher Algorithm", Network and Complex Systems, Vol. 3, No. 8, pp. 1-5, 2013.
- Md Imran Alam, "A Comparative Analysis of Different Encryption Techniques of Cryptography", International Journal of Advanced and Innovative Research, Vol. 2, Issue 9, pp. 160-166, 2013.
- Ali M Alshahrani, "Different Data Block Size Using to Evaluate the Performance Between Different Symmetric Key Algorithms", International Journal of Computer Networks and Communications, Vol. 6, No. 2, pp. 89-97, 2014.
- William Stallings, "Cryptography and Network Security", Fifth Edition, Pearson Publication, Prentice hall, 2013.
- Neeraj Khanna et al, "New Symmetric key Cryptographic algorithm using combined bit manipulation and MSA encryption algorithm: NJJSAA symmetric key algorithm, IEEE, pp.125-130, 2011.
- Manikandan G, Rajendran P, Chakarapani K, Krishnan G and Sundarganesh G, "A Modified Crypto Scheme for Enhancing Data Security", Journal of Theoretical and Applied Information Technology, Vol. 35, No.2, pp.149-154, 2012.
- Ashwak Alabaichi, Faudziah ahmed and Ramlan Mahmod, "Security Analysis of Blowfish algorithm", IEEE, pp. 12-18, 2013.
- Monika Agrawal and Pradeep Mishra, "A Modified Approach for Symmetric Key Cryptography Based on Blowfish Algorithm", Internat ional Journal of Engineering and Advanced Technology, Vol. 1, Issue 6, pp. 79-83, 2012.
- Israa Tahseen and Shatha Habeeb, "Proposal New Approach for Blowfish Algorithm by Using Random Key Generator", Journal of Madent Alelem College,Vol. 4, No. 1, pp. 1-10, 2012.
- Ratinder Kaur and V. K. Banga,"Image Security using Encryption based Algorithm", International Conference on Trends in Electrical, Electronics and Power Engineering (ICTEEP'2012), pp. 110-112, 2012.
- B.Geethavani, E.V.Prasad and R.Roopa, "A New Approach for Secure Data Transfer in Audio Signals Using DWT", IEEE, 2013.
- Bruce Schneier, “Applied Cryptography”, John Wiley & Sons, 2nd Edition, New York, 1996.
|