International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Menu

ISSN ONLINE(2320-9801) PRINT (2320-9798)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

PAPR Reduction in OFDM System Using Enhanced PTS Algorithm

Misha Arora, Er.Parvinder Singh
  1. M Tech Scholar, RIEIT , RailMajra, Punjab, India
  2. Asst. Professor, RIEIT , RailMajra, Punjab, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Abstract

OFDM system is known for its high data rate transmission and to send the data in a bulk amount. But advantages results into some drawbacks also . One of the major drawback of OFDM systems is Peak Average to Power Ratio (PAPR) which is caused due to the high power amplifications of the signal passing through the OFDM system. This paper focuses on the reduction of the PAPR in OFDM system which uses AWGN channel for its transmission using a compound technique of PARTIAL TRANSMIT SEQUENCE (PTS ) by changing the phase modification in which the PTS occurs.



Keywords
OFDM , PAPR , AWGN , PTS

INTRODUCTION
OFDM is a special case of multicarrier transmission, where a single data stream is transmitted over a number of lower rate subcarriers[1]. The main advantages of OFDM are its increased robustness against frequency selective fading or narrowband interference as well as the efficient use of available bandwidth. Two major drawbacks of OFDM systems are the great sensitivity to time and frequency synchronization errors, and the high PAPR. Due to high PAPR, the amplified signal suffers from distortion and outof- band noise when passed through nonlinear devices, such as a Power Amplifier (PA). A solution to this problem is the use of highly linear Power Amplifiers (PA) with sufficient back-off. However this solution comes at the penalty of high power consumption and it also leads to one of the major problems of OFDM systems called PEAK TO AVERAGE POWER RATIO [1,2,3,4] (PAPR).There are several techniques to reduce the PAPR in OFDM system like Clipping , SLM , PTS etc.
PAPR IN OFDM : Generally each and every system has a pattern of transmitting and receiving the data[2]. OFDM is no where different. It works according to the following block architecture.
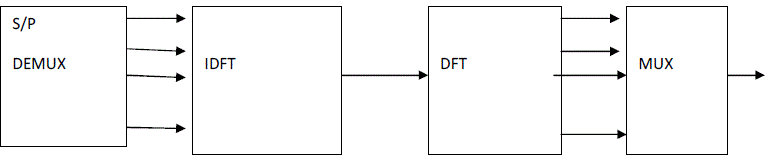
The block diagram of OFDM system is shown in figure 1. The transmit signal can be generated by a simple IDFT operation, which can replace the bank of modulators [2] and at the receiver; a DFT can be performed to recover the transmitted signal. OFDM signal consists of n data symbols transmitted over N0 subcarriers. Let P = { Pk, k=0, 1,2,--,N0- 1} be a block of n data symbols and each symbol modulating a set of subcarriers {fk, k=0,1,- -,N0-1}. PAPR of the OFDM signal x (t) is defined as the ratio between peak power and its average power during the OFDM signal.[4]
PAPR= |x | peak 2 / |x| rms2 [7] where rms is the root mean square value of the obtained signal.
The PAPR of the continuous-time OFDM signal cannot be precisely computed in the Nyquist sampling rate, which corresponds to N samples per OFDM symbol. In this case, signal peaks may be skipped and PAPR estimates are not precise. So, oversampling is necessary.
To evaluate the PAPR reduction performance accurately from the statistical point of view, the complementary cumulative distribution function (CCDF) of the PAPR of OFDM signals is used. CCDF describes the probability of exceeding a given threshold PAPR0 and is represented as
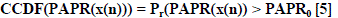image
Due to the independence of the N samples, the CCDF of the PAPR of single input single output (SISO) OFDM as a data block with Nyquist rate sampling is given by
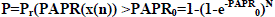image
PTS: Stands for PARTIAL TRANSMIT SEQUENCE. In PTS scheme, an input symbol sequence A is partitioned Into V ‘disjoint’ symbol subsequences
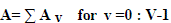image
Here, the word ‘disjoint’ implies that for each given k,0 < k<=N-1 , A v,k=0 except for at most a single . In other words, the support sets of are disjoint. The signal subsequence is generated by applying inverse fast Fourier transform (IFFT) to each symbol subsequence av, often called a sub block. Each signal subsequence is then multiplied by an unit magnitude constant chosen from a given alphabet , which is usually Z={+-1 }or {+-1 ,+- j } and summed to result in a PTS OFDM signal sequence which can be expressed as
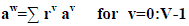image
The known sub block partitioning methods [6] can be classified into three categories. The first and simplest category is called an adjacent method which allocates successive symbols to the same sub block. The second category is based on interleaving. In this method, the symbols with distance are allocated to the same sub block [8]. The last one is called a random partitioning method in which the input symbol sequence is partitioned randomly. For example, let us partition an input symbol sequence of length 16 into 4 symbol subsequences. Then, is used as a sub block partitioning sequence for the adjacent method, for the interleaved method, and for the random method. The PAPR reduction performance and the computational complexity of PTS scheme depend on the method of sub block partitioning. In other words, there is a trade-off between PAPR reduction performance and computational complexity in PTS scheme. The random partitioning is known to have the best performance in PAPR reduction. The interleaving method [5] can reduce the computational complexity of PTS scheme using Cooley-Tukey FFT algorithm, but the PAPR reduction performance is the worst.[9, 10]

PROPOSED PTS METHOD
The existing novel PTS Scheme is based on the phase factors. With two phase -1 and 1 results in four phase factors b1={1,1} , b2={1,-1} , b3={1,j} and b4={1,-j}.[1] These phase weight vectors helps in finding the appropriate threshold according to the weight generated at these phase vectors mentioning that for the adjacent phase weighting vectors in same column , only the sign of one element is different. In our proposed scheme we have introduced a phase 0 (zero ) in the existing phases as sign of zero can neither be considered as positive nor negative and it would result in better search threshold values.
With the introduction of 0 in the phase vector , we would be getting the following phase factors {1,1} ,{1,-1} ,{1,j} , {1 -j}, {0, j} , {0, -j} and hence it would result into a better PAPR reduction value.
The parameter P introduced in novel PTS method [1] would be re written as follows
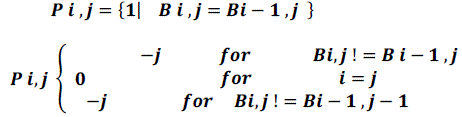image

RESULTS AND CONCLUSION
Our proposed scheme results into an efficient reduction scheme whose results are discussed as follows.
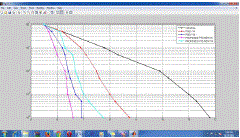
Figure represents the results of enhanced PTS scheme which indicated that with an increased phase factor the value of PAPR is reduced.
By comparing of the PAPR reduction performance with different sub blocks in Figure it is clear that PAPR is decreased from 8.8 dB to 7.8 dB for V4. For V6 the resulting value has been decreased from 6.9 to 6.65. Our current approach opens up a lot of future possibilities for the future research workers. Our current system does not include a lot of modulation techniques like QAM 16 , 32 and 64 which may enhance the result.

Figures at a glance
Figure 1 Figure 2 Figure 3
Figure 1 Figure 2 Figure 3

References