International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Menu

ISSN ONLINE(2320-9801) PRINT (2320-9798)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Parallelization of Biological Gene Sequencing Technique with Optimized Smith Waterman Algorithm

Ananth Prabhu G1, Dr. Ganesh Aithal2
  1. Assistant Professor, Dept of CS&E, Sahyadri College of Engineering & Management, Mangalore, India
  2. Professor, HOD CS&E, P.A. College of Engineering, Mangalore, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Abstract

The presented research work represent a highly robust and efficient parallel computing system development for biological gene sequencing. In this research work, the existing approaches has optimized the most optimum approach available till date in the form of Smithy Waterman algorithm for gene alignment or local gene sequencing. This paper mainly emphasizes on the system development for a traceback assisted optimum diagonal sequencing approach developed with optimized smith Waterman and Myers and Millers techniques. Considering optimization approaches it can be firmly stated that the presented work not only enhances the competing efficiency but also facilitates higher optimum memory occupancy for huge data sets and pattern possibilities.

Keywords
Smith-Waterman (SW), Myers-Miller Algorithm, Diagonal Parallel Sequencing and Alignment Approach (DPSAA), Dynamic programming, Backtracking, Pseudo code

INTRODUCTION

Biological Sequence Alignment
To compare two sequences, we need to find the optimal alignment between them, which is to place one sequence above the other making clear the correspondence between similar characters. In an alignment, spaces can be inserted in arbitrary locations along the sequences. Basically, an alignment can be:
1) Global, containing all characters of the sequences;
2) Local, containing substrings of the sequences; or
3) Semi global composed of prefixes or suffixes of the sequences, where leading/trailing gaps are ignored.
In order to measure the similarity between two sequences, a score is calculated as follows: given an alignment between sequences S0and S, the following values are assigned, for instance, for each column:
1) ma =+1, if both characters are identical (match);
2) mi =-1, if the characters are not identical (mismatch); and
3) G =-2, if one of the characters is a space (gap).
The score is the sum of all these values. Figure 1 presents one possible alignment between two DNA sequences and its associated score. In Figure 1, a constant value is assigned to gaps. However, keeping gaps together generates more significant results, in a biological perspective [1]. For this reason, the first gap must have a greater penalty than its extension (affine gap model). The penalty for the first gap is G first and for each successive gap, the penalty is Gext. The difference G first – Gext is the gap opening penalty Gopen.
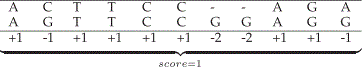image
Figure 1: Alignment and score between sequences S0and S,
In the proposed system model, the implementation of Smith Waterman algorithm has been taken place in two consecutive steps.
1. Calculate the DP matrices
2. Obtain the optimal alignment
The first phase of the algorithm receives as input sequences S0 and S1, with sizes m and n, respectively. For sequences S0and S, there are m+1 and n+1 possible prefixes, respectively, including the empty sequence. The notation used to represent the nth character of a sequence seq is seq[n] and, to represent a prefix with n characters we useseq[1, n]. The similarity matrix is denoted H, where Hi,j contains the similarity score between prefixes S0[1. . i]and S1[1. . j].
At the beginning, the first row and column are filled with zeroes. The remaining elements of H are obtained from (1), where p(i; j) = ma (match) if S0[i] S1[j] and mi (mismatch) otherwise. In order to calculate gaps according to the affine gap model, two additional matrices E(2) and F(3) are needed. Even with this, time complexity remains quadratic.
The optimal score between sequences S0 and S1 is the highest value in H and the position (i , j) where this value occurs represents the end of alignment
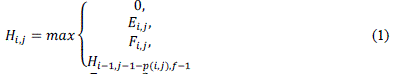image
image
image
Step 2. (Obtain the optimal alignment).
To retrieve the optimal local alignment, the algorithm starts from the cell that contains the highest score and follows the arrows until a zero-valued cell is reached (Fig. 2). A left arrow in Hi,j indicates the alignment of S0[i] with a gap inSi. An up arrow represents the alignment of Si[j]with a gap in S0. Finally, an arrow on the diagonal indicates that S0[i]is aligned with Si[j]
image
Figure 2 : DP matrix for sequences S0and S1. Bold arrows indicate the traceback to obtain the optimal alignment.

LITERATURE SURVEY
Hsien-Yu Liao et al [37] advocated a scheme for biological gene sequence using Smith-Waterman algorithm which takes into consideration of the dynamic programming approach possessing higher sensitivity. In their work, they facilitated a significant enhancement in enhancing execution speed and it exhibited its superiority over the conventional sequential approach, while preserving similarity in its functional and performance sensitivity.
Arpit, G. et al [38] developed a noble architecture called Diagonal Linear Space Alignment algorithm that was the enhanced form of FastLSA. The unique and robust approach developed was capable of performing with higher datasets sizes. Then also this approach performs process for storing data of the diagonals of the Dynamic Programming matrix in different way as it is done with FastLSA that exhibits storing of the rows and columns. The researchers have analytically and experimentally proved that their algorithm performs better than FastLSA.
Gardner-Stephen et al [40] developed an algorithm for genomic and proteomic sequencing called DASH. The developed scheme consequences into better performance in terms of higher execution speed as compared to reference system NCBI-BLAST 2.2.6. The implementation of dynamic programming causes much enhancement that enhanced system for its highly robust and effective items exploration. Improving the efficiency of DP provides an opportunity to increase sensitivity, or significantly reduce search times and help offset the effects of the enduring high rate growth with varying datasets of different sizes.
Aji, A.M. et al [41] presented n extremely glowing well prepared organize parallelization of the Smith-Waterman algorithm at the Cell Broadband Engine phase, a new cross multicore structural design that constrain the low − cost Playststation 3 (PS3) play game comfort and the IBM BladeCenter Q22, that presently powers the greatest supercomputer into the world, Roadrunner on Los Alamos National Laboratory. During an inventive mapping of the most favorable Smith-Waterman algorithm on top of a cluster of PlayStation PS3 nodes, in this research completion delivers twenty one to fifty five folds up speed above an elevated end multicore structural design as well as up to 449 − fold speed-up in excess of the PowerPC processor inside the PS3. Subsequently, the researchers estimated the trade-offs flanked through their Smith- Waterman completion on the Cell with obtainable software in adding up to hardware implementations as well as illustrated that the explanation achieves the most outstanding performance-toprice ratio, whilst aligning realistic series dimension and generating or forming the authentic alignments. At last, the researchers demonstrated that the low-cost explanation on a PS3 cluster advance the speed of BLAST while attain ideal compassion. To enumerate the association between the 2 algorithms in conditions of speed as well as sensitivity, the researchers formally describe as well as enumerate the sensitivity of homology investigate techniques so that trade-offs among sequence-search explanation can be appraise in a quantitative method.
Riedel et al [58] concentrated on the spatial action appreciation problem with an algorithm pedestal on Smith- Waterman (SW) local arrangement. The projected Smith-Waterman (SW) technique consume vibrant programming with 2 dimensional spatial information to enumerate progression comparison. Smith- Waterman (SW) is glowing suited for spatial action appreciation as the technique is healthy to sound as well as can provide accommodation gaps, consequential from roadway system mistakes. Different other techniques Smith- Waterman (SW) are capable to locate as well as measure behavior entrenched within irrelevant spatial data. During testing with 3 class data information set, the researchers demonstrated the presented Smith-Waterman (SW) algorithm is competent of identifying precisely as well as imprecisely segmented spatial sequences. To standard the methods classification presentation the researchers evaluated it to the separate hidden markov model (HMM). Results demonstrated that Smith-Waterman (SW) demonstrate higher correctness than the hidden markov model (HMM), in addition to maintains superior classification accurateness with small training set size.
Cehn, C et al [75] presented an algorithm to compute the optimal and near-optimal alignments of two sequences in linear space and quadratic time. The researchers demonstrate how this algorithm can be parallelized efficiently on a PC cluster and on a computational grid in order to reduce its runtime significantly. The grid implementation uses a hierarchical approach combining inter-cluster and intra-cluster parallelism.
Batista, R.B et al [76] proposed the algorithm planned by Smith-Waterman is a precise technique that gets hold of most favorable local alignments in quadratic liberty and moment. For extended sequences, quadratic difficulty creates the employ of this algorithm not convenient. During this situation, parallel computing is an extremely attractive substitute. In this paper, the researchers propose and evaluate z-align, a parallel exact strategy based on the divergence concept to locally align long biological sequences using an affine gap function. Z-align runs in limited memory space, where the amount of memory used can be defined by the user. The results collected in a cluster with 16 processors presented very good speedups for long real DNA sequences. By comparing the results obtained with z-align and BLAST, it is clear that z-align is able to produce longer and more significant alignments

Myers-Miller and Trace-Backing Algorithm
For long sequences, space is a limiting factor for the optimal alignment computation. Myers and Miller (MM) is the algorithm that computes optimal global alignments in linear space. It is based on Hirschberg [101], but applied over Gotoh [102]. Hirschberg’s algorithm uses a recursive divide and conquers procedure to obtain the longest common subsequence. The idea of this algorithm is to find the midpoint of the LCS using the information obtained from the forward and the reverse directions, maintaining in memory only one row for each direction (thus in linear space). Given this midpoint, the problem is divided in two smaller sub problems that are recursively divided in more midpoints.
The MM algorithm works as follows.
Let S0and S1 be the sequences, with sizes m and n, respectively, and i*= m/2
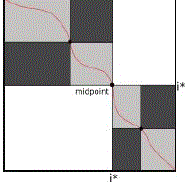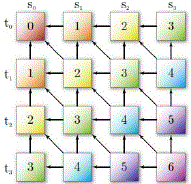
image
Figure 3: Recursive splitting procedure in MM.
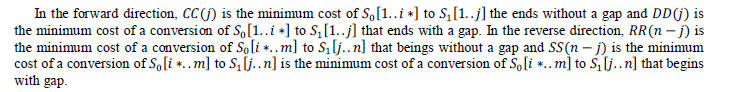image
To find the midpoint of the alignment, the algorithm executes a matching procedure between:1) vectors CC and RR;2) vectors DD and SS. The midpoint is the coordinate (i*,j*), where is the position that satisfied the maximum value in (4).
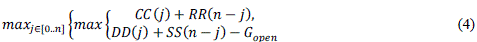image
After the midpoint is found, the problem is recursively split into smaller subproblems (Figure 4.3), until trivial problems are found. The matching of CC with RR represents a junction of the forward alignment with the reverse alignment without a gap and the matching of DD with SS represents the junction with a gap. When there is a gap in both directions, both receive a gap opening penalty, so this duplicated penalty must be adjusted.

System Modeling with SW algorithm
A brief and the generic function of Smith Waterman approach has already been discussed in previous chapter with its general characteristics and its implementation for performing parallel computing in case of gene sequencing or gene alignments applications. The SW technique performs computation for the optimal local alignment for certain pairs of data sequences as per the scoring mechanism presented by a substitution matrix and certain function named as gap penalty function. Another matrices function called substitution matrices refers for a symmetric matrix which performs assignments of the cost of gene sequential pairing bases collectively. Ultimately the computational costs are estimated from certain analyzed and retrieved substitution occurrences in data alignments for the associated data or biological sequences. The individual effective data pairs is provided certain scores that represents the observed occurrences of these kinds of occurrence in sequential alignments of evolutionarily associated data sequences. The retrieved data sets also represent the sample frequency for individual bases as few bases emerge more abruptly as compared to other. The identities are normally allotted its respective maximum possible scores, frequently occurred substitutions also take delivery of derived or assigned positive scores, but performs or exhibits matches which comes into existence in highly improbable are penalized by certain negative scores. The approach of Smith-Waterman also backs up the penalty gaps in the data sequences so as to optimize or maximize the substitution matrix. The system parameters possessing the gap penalty function affect the gap’s length and its frequency applicable with data or sequence alignment.
In general there are three kinds of gap penalty functions. There are as follows:
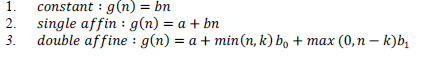image
The definite or fixed gap function permits a constant cost to individual gap position, irrespective of its placement in the sequential alignment. The solitary affine gap function performs penalization on the gap generation so as to persuade the assignment of new gap locations for extending the available gaps in spite of forming any new ones. It becomes a more believable framework for gaps in biological sequences as a gap multiple could be taken into consideration by a unitary evolutionary event. This approach is then extended by the double affine gap function by exhibiting certain individual gap penalty for every gap space which do extend a gap further than the threshold of those spaces; is frequently set lesser than to persuade gaps of longer length. In this research work, the author has implemented this function because it strengthens the generalization of both the fixed variables and unitary (single) affine gap functions. The most favorable sequence alignment to this scoring approach is established by estimating a set of repetitive associations over individual cell of the Dynamic Programming (DP) lookup table.
For illustration, the below mentioned expression estimates the optimum associations by implementing optimized alignment scheme with the single affine gap penalty function:
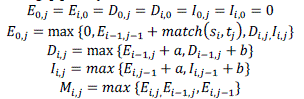image
image
Figure 4: Illustration of data dependency for Dynamic programming.
In above presented figure 4 it can be visualized that the cells from individual diagonal are mutually independent, and these all depend on cells from its last two diagonals.
Consider, 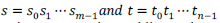image refers the two input data sequences, which do performs matching for the substitution cost matrix a while another variable b refers for the single affine penalties function used for formation and extension of gaps. Taking into account of the double affine gap penalty function there is the need of the transitional gap lengths for associating with D so as to choose the optimal penalty for b. The predominant objective of M is to perform tracking of the highest alignment matrices or score for all comprising cells in the dynamic programming table. Here the ultimate optimal alignment score would be propagated to the last cell matrices , j . The pointers for individual variable or cell M i; j it is always maintained to perform tracking of the cell location with the highest possible score for alignment and for simplifying the tracking of alignment with trace back step.
The following figure (Figure 5) presents the data dependencies considered for estimating the recurrence relations across the dynamic programming look up table. In case of certain system functional on single processor, the dynamic programming lookup table are processed in sequential way but the same in multiprocessor based system, it can be exploited efficiently for its data dependencies while exhibiting certain independent cells from individual dynamic programming table in diagonal parallel block (up to min(m; n) cells) in parallel fashion. Additionally, the other contribution of data dependencies can be signified in terms that this nature permits opportunities for cache optimization and for it only two diagonals are processed while exhibiting a computation pass so that a adequately large cache can optimize the cache coherency.
Possessing p = min(m; n) processors, the dynamic processing lookup table might be effectively estimated in (m + n; 1) passes by performing sequential processing with individual diagonal parallel cells. Regrettably, there exists some decay in loss as some processors must stall when exhibiting non-major diagonal. And in such scenario, the highest or total count of stalls in the dynamic programming computation could be p(p1). then while, the query sequence is in general exhibited for matching against the database of multiple target sequences, and thus the estimation of dynamic computation tables can be processed with interleaving together so as to amortize the processor stalls.
image
Figure 5: Presentation of data dependency (a) Permits cell estimation for assigning a set of processors. (b). The exhausted cell or space which can be effectively amortized over multiple query sequence comparisons by joining their respective dynamic programming look up table as presented in figure (c).
In this work and the prepared thesis, the author has not only enhanced the pattern alignment with a novel diagonal sequencing patter but also has made enhancements in Smith Waterman techniques while taking into account of Myers and Millers technique for performing traceback and reverse and diagonal sequential alignment. The novelty of this research work was rooted with the development of a parallel and diagonal sequence alignment system that could perform far better than other existing approaches with serial and parallel alignments.
In order to accomplish this goal, the author has incorporated few enhancements in terms of optimized midpoints estimation, optimum averaging, and trace backing facility and sequential distance estimation for traceback in reverse as well as forward sequence so as to accomplish diagonal alignments and parallel computing. The ascending section would represent the algorithmic development made for accomplishing research objectives and dominant system enhancements.
The enhanced the generic local gene sequencing approach by means of a highly robust and optimized traceback facility and memory optimization. This is being done while taking into account of Myers and Millers techniques. In order to accomplish the overall objectives, here in this research work, the author optimizes every encompassing components or factors that could effectively enhance the gene alignment and most optimum computing facility. The consideration of Myers and Millar algorithm made this system very effective for minimizing space constraints and thus the overall system was emerged out to be highly effect in terms of least memory utilization, wise alignments, path tracking, trace path detection, midpoint calculation etc, which ultimately played a significant role in gene sequencing with Smith Waterman (SW) approach.
The following section elaborates the factors developed and optimized so as to accomplish the ultimate objectives of the research work.

Intra-Task kernel enabled Backtracking
The sequence alignment problem is to find the optimal alignment between a query sequence q of length m symbols and a database sequence d of length n from some alphabet A. In most bioinformatics applications, A consists of symbol representing amino acids or nucleotides. To determine the score of a particular alignment, a scoring function 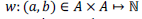imageis used to score each pair of symbols in the alignment. A gap open penalty ρ, and a gap extension penalty σ, are commonly used to penalize gaps of unpaired symbols.
In the implemented Smith-Waterman (SW) algorithm which is a dynamic programming algorithm which will determine the optimal local alignment between q and d given w, p, and σ. SW fills in three M× N tables E, F and H as shown in equation mentioned below. The optimal alignment score is given by the maximum score in table H. The dependencies for a cell in H are shown in Figure 6.
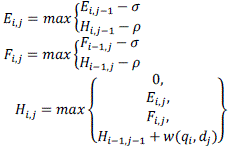image (5)
The optimal alignment can be found by backtracking through H, but for comparisons of a query sequence to an entire database, we are generally only concerned with the score and not the actual alignment. The table can be computed with computational complexity of O(nm) but, when only the optimal score is required, the space complexity is linear.
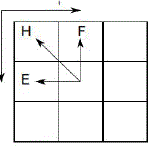image
Figure 6 : Dependencies for a cell in H of the Smith Waterman algorithm.
Although the cell updates are vectorized, the similarity function lookup is sequential. To address this problem, a query profile creates a vectorized lookup table for the similarity scores that is unique for a given query sequence. The query sequence is split into pieces with length equal to the vector length used by Streaming SIMD Extensions (SSE). The profile is built by storing vectors of similarity scores for each piece of the query sequence compared to all symbols in the alphabet. This allows similarity function lookups to be performed in parallel. Existing approaches in general use a query profile in the inter-task kernel and we make use of the query profile in our improved intra-task kernel compare a single query sequence to a database of sequences. Each kernel uses a different strategy to find the optimal score. For each query/database sequence pair, only one kernel is used. If the database sequence length is below 3072, the intertask kernel is used. Otherwise, the intra-task kernel is used. The author in this research work has employed improvements solely in the intra-task kernel.

Inter-task:
The inter-task kernel uses a single thread to compare a query and a target sequence. It tiles the tables into 8×4 tiles which are computed sequentially by the same thread in row major order. The thread will compute each cell in a tile in a column major order, storing all values needed for dependencies within a tile in registers. Once a tile is computed, the bottom row is stored in global memory and the rightmost column is stored in registers to satisfy the dependencies required by bordering tiles.

Intra-task:
The intra-task kernel uses an entire thread block to find the optimal alignment score between a query sequence and database sequence. No tiling is used and the table is computed in the usual wavefront parallel. Therefore, all threads in the block are busy only when the length of the minor diagonal is a multiple of the number of threads per block.
In the ascending section of the presented manuscript, the author has provided a detailed algorithmic development for exhibiting sequential pair alignment with intra-task kernel based parallelization scheme with optimized Smith Waterman (SW) algorithm.

Sequence Distance Computation
Calculation of edit distances between two sequences and aligning the two sequences based on their edit distances is a very compute intensive process. This problem becomes n-fold when the number of sequences on which these operations have to be done are huge. Many fields have hence refrained from using edit-distance as a possible solution to solve problems. Therefore in this work the author has incorporated an optimization approach for sequential distance computation associated with the computational matrices and nodes.
This is the matter of fact that for accomplishing an efficient sequential distance computation there is the need of a potential approach of pairwise genes alignments and in order to get it here in this thesis the author has develop and optimized an approach of pairwise alignment that could be a significant factor to compute the edit distance between two sequences and then align these sequences with an allowed fixed number of insertions, deletions and mismatches. Edit distance computation between two sequences also finds its applications in other domains. Few approaches such as edit-distance algorithm to detect correlated attacks in distributed systems was explored in our work while extracting the benefits of edit distance technique to identify the type of intrusion. The motive of employing edit distance approach was to find how close two strings are from each other and auto-check the spelling of the word accordingly. This process involved the calculation of edit distances between millions of sequences and then the alignment of these sequences. An interesting application of edit distance and alignment of two sequences is in Bio-Computation. The machines which generate the DNA data have progressed at a much rapid pace than the techniques to analyze this data. This was in fact a profound problem in our processed bio-computation domain. In the ascending section the details of algorithmic development for pairwise alignment has been provided.

Pairwise Alignment
The system development approach for the proposed pairwise alignment has been presented as follows.
Given two sequences D and Q with lengths Ld and Lq, respectively, their genetic distance can be estimated by the following mathematical expression.
image
image
Figure 7 illustrates the pseudo code for the SW algorithm of the proposed implementation. The proposed method is an improved version based on the implementation introduced in chapter 3, where different pairs of sequences is assigned to different warp of threads. For each individual warp, threads cooperate and communicate through shared cache with no thread synchronization procedures. As shown in Figure 4.8, the alignment matrix is divided into parallelograms so that the computation is classified into three stages.
Let 2 × 32 shared memory blocks store each subsection of database sequences and let 32 registers store each subsections.
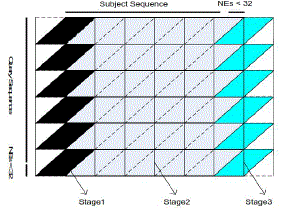image
image
Figure 8: The architecture of the computational matrix for each pair of sequences
In stage1, the first 32 memory spaces c[tid] are initialized as 0, which denotes no input. The following 32 memory spaces c[tid + 32] then load subject characters. The bottom row of the first parallelograms is processed by tid_31. The range of characters processed is from c_0 to c_31.
In stage2, c[tid + 32] pass characters into c[tid] before they read new characters.
In stage3, c[tid + 32]pass characters to c[tid] before they are set to 0, which denotes dummy characters. Cells in the bottom row of the warp alignment matrix in Figure 8 are firstly passed into shared memory by the 32th thread and written into global memory in two write operations by halfwarp of threads afterwards.
The pseudo code in Figure 7 regarding the computation of the most inner loop is called in each stage with different subsection of the subject sequence. The intermediate data, H and F, within each parallelogram are transferred through shared memory. The swap of H and F for the next sub-section of query sequence is firstly passed into shared memory and then stored in global memory. The computations of diagonal i depend on the values of diagonal i– 1 and diagonal i–2. Therefore, the overall alignment score in the alignment matrix can be found in linear memory space. After that, the implementation is scaled up to calculate the exact matched characters between the optimal local alignments using the Myers-Miller algorithm, which was proposed to decrease the memory complexity from O(Ld × Lq) to linear memory space O(Lq) for optimal alignments.
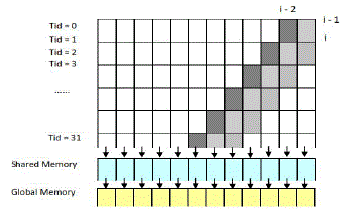image
Figure 9: Data dependency among cells and memory hierarchies

Searching optimal midpoints
As described above, the local optimal regions of the alignment matrix can be calculated by two pairwise alignment implementations, one forward and one reverse. The actual trace path can be found using the Myers-Miller algorithm. As explained above, the central idea of the algorithm is to search recursively for optimal alignment residues, which are the midpoints of an optimal conversion using a forward and a reverse cost-only pairwise alignment. The below mentioned expression gives the number of matched characters between two sequences:
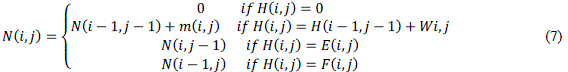image
Here m(i, j) is equal to 1 if d= qj and 0 otherwise. From above mentioned mathematical expression, the maximum N (i, j) stands for the number of matched characters in O(Lq) memory space. Since the memory consumption for this approach grows quadratically with the length of sequences, the number of parallelizable threads is limited in this method. Therefore, this approach can be performed, but definitely infeasible to achieve high performance acceleration results. Performance significantly degrades when aligning datasets having long length of sequences. One of the predominant limitations of the majority of existing approaches was somewhat allied with linear memory space and thus computational complexity. Therefore as discussed already that the author in order to eliminate such kind of shortcomings in the existing approaches the author in this thesis has employed highly robust Myers-Miller algorithm to conquer the problem in linear memory space. These are Inter-task parallelization strategy and Intra-task parallelization strategy respectively. The former harnesses single thread to process a specific problem in an application, while the later harnesses a block of threads to divide a specific problem into sub problems with each thread processing relevant sub problems. While taking into account of inter-task parallelization approach the author realizes the dominant drawback of it in the form of computing optimal midpoints in this implementation which is caused by the insufficient various numbers of cells for each recursion. For instance, given two sequences D and Q, composed of identical characters and having the same length L (L = 40), the computation order of midpoints in both D and Q and the number of characters involved in each recursive operation. The maximum size and the minimum size of the matrix computed in the forward pass and reverse pass are 1600 and 4 respectively. Therefore, the number of characters involved varies considerably and given a fixed number of threads, loss of performance is inevitable because of thread load imbalance in the search of optimal midpoints. The computation leads to idle operations of threads when the number of threads is bigger than the characters in each sub section of D or Q. The actual thread usage ratio degrades to 1 / �� when computing a sub-section with only one character, where N is the number of threads allocated to process each sub matrix.
In this research work, in order to accomplish higher and optimum system model and sequential alignment facility the author also incorporated a system modelling for improved Intra-task parallelization strategy. Above all, one of the sequences in the sequence pair is chosen and recursively divided into segments of equal lengths. This operation stops once the length of the final segment is shorter than a threshold value T. As such, the number of the potential blocks separated from the entire matrix can be predicted. The optimal midpoints in another sequence can be calculated one by one using Myers-Miller algorithm. Then, cells in each sub-matrix are computed with their alignment directions stored in shared memory so that the trace path can be accessed later. The strategy uses the Intra-task parallelization approach and Myers-Miller algorithm. The uniqueness of this proposed approach was that this system does not compute all midpoints as a profile for the requirement of trace path can be obtained by concatenating several points on sequences. Firstly, a subject sequence in a pair alignment is divided by the number of threads until the length of the final segment is smaller enough so that its matrix alignment can be stored in shared memory. The number of midpoints can be deduced from the number of divisions performed. Secondly, midpoints on the query sequence corresponding to those on subject sequences in the same pair can be found through forward phase computations and reverse phase computations. �� trace belt (see shaded area in Figure 10) is then obtained by linking all corresponding midpoints on the sequences. Until now, the actual trace path still has not been found, but it is obvious that the trace path should be within the trace belt. In some cases, the interval value between two neighbouring midpoints in query sequences is bigger than the number of threads, which is possible if there are enough gaps in subject sequences. Therefore, the query segment needs to be divided until it is small enough for shared memory data storage. Blocks composing the trace belt are then computed one by one with directions stored in shared memory. The overall trace path is the concatenation of all small trace paths in sub blocks.
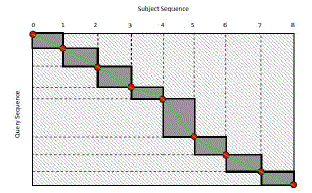image
Figure 10: Trace belt of the alignment matrix
The algorithms developed for trace-backing or trace belt has been given in Figure 11. Firstly, the number of sub blocks is calculated using the length of subject sequence. This is achieved by recursively dividing the subject sequence in two until the length of resulting sub-sequence is equal to or smaller than the width of matrix in shared memory. r_no = 1 means that the final number of sub-blocks is equal to 1 if the length of query sequence is small enough. Otherwise, the size of alignment matrix outstrips the storage of shared cache. In this case, the whole matrix is loaded and passed by the forward and reverse computation to find the optimal mid-point on query sequence after the determination of the midpoints on subject sequence. The latter is defined as half the size of the subject sequence in the first computation. C, I, R and S are vectors.
image
Figure 11: Pseudo code of computing optimal mid points in our proposed method.

Optimal alignment trace back
Up to this point, the full trace path has not found yet as not all midpoints have been computed. Figure 12 presents the pseudo code of alignment trace back for each sub-block. Though preliminary trace profile composed by sub blocks has been found, sub-blocks still cannot be put into shared memory if their heights are larger than the number of threads, which occurs when the length of the sub query sequence is longer than the corresponding length of the sub subject sequence and optimal alignments need to insert gaps in subject sequences. This is not common in homogenous sequence databases, especially in local alignments. However, for databases composed of heterogeneous sequences, there are usually gaps in a pair of optimal alignment. Here, it is necessary to check the sub-length of query sequence for the purpose of doing the final alignment by executing the pseudo code in Figure 12. Here, we divide the query sequence rather than the subject sequences. Afterwards, each sub-block is passed through the pseudo code in Figure 10 with the directions of aligned cells stored in shared memory. In the proposed approach, constants 1, 2 and 3 are used to denote the left, upper and upper-left directions respectively. The starting point is initialized as 0. Finally, the optimal alignment can be found by tracing from the cell in the bottom-right corner to the cell in the upper-left corner in the shared memory. The shared memory is then used iteratively for the next sub-matrix.
image
Figure 12: Pseudo code of computing matched characters of sequences in a pair. Vectors recording trace path are needed in the stage of progressive alignment.

Guide tree
The Neighbor-Joining (NJ) method [103] is used to construct an un-rooted tree. Exhaustive distances between nodes are traversed from the distance matrix to identify two closest nodes at each step. For a set of sequences N, the number of distances between each pair is N * (N - 1) / 2. The traversal finds the smallest distance value and combines two closest nodes into a new node until N is equal to 1. An un-rooted tree is produced by the NJ method. Since the percentage of time consumed on the construction and rooting of guided trees is relatively small.

Parallelization of Progressive Alignment
The stage of progressive alignment performs profile-profile alignment on the guided tree starting from leaf nodes up to the root node. Leaf nodes stand for the original sequences which are the initial descendent nodes composing internal nodes. The latter are produced by two aligned nodes. For each internal node, there are three combination alternatives on their descendents, namely 1) two sequences, 2) two nodes, and 3) one node with one sequence. Internal nodes can be aligned only when their left sub node and right sub node have been performed. Therefore, the computation order of nodes can be parallelized using parallel processing batches. Nodes with their left sub node and right sub node performed can be computed in the same batch. In the proposed method, the progressive alignment of the guided tree can be performed by the following steps:
Firstly, a dependency structure corresponding to each node of the guided tree is created and used to store the attributes of each node. For each internal node, the structure contains its left descendent, right descendent and an aligned flag bit which denotes whether the node is in the waiting queue or not. For each leaf node, its left children and right children are set to 0 as it has no descendents. The flag bit is set to 1 automatically. The first launch is always performed on the internal nodes where both descendents are sequences. The pseudo code in Figure 12 presented the trace back procedure on each sub-trace. For the progressive alignment, there are some differences with the pseudo code presented in Figure 12, as not only optimal alignment scores but also optimal alignments need to be passed to the host in this instance. Hence, for each pair of profiles, the number of gaps between two alignments is accumulated exactly on specific positions and stored in two gap list vectors in global memory. Based on these lists, optimal alignments corresponding to nodes in pairs can be constructed on the host. The aligned descendents of nodes are packed into new profiles. Their aligned flags are then set to 1 and are added into a ready queue for the next launch. These operations are performed iteratively until all internal nodes are aligned.

RESULTS
In the presented work a highly efficient and optimized scheme for biological gene sequencing with optimized Smith Waterman algorithm functional with Myers Miller approach and Intra-Task parallelization scheme is developed. In this work, a complete system model with a goal to come up with a Diagonal sequencing approach that can perform better than the existing serial or parallel sequencing techniques. This is matter of fact that the architectural and processing sequences in case of proposed model, causes the estimation of parametric matrices very easy such as optimal mid-point estimation, optimum trace-back approach that employs reverse and forwards diagonal sequencing etc. The overall system uniqueness has been ground rooted with Smith Waterman algorithm and for optimizing the limitations of memory factor; the author has employed the Myers and Miller algorithm for all simulation scenarios.
In system simulation phenomenon the three system models are developed. One for serial sequencing while second advocates parallel sequencing and processing approach while the third one represent the novel system proposed by author in terms of diagonal sequencing. The overall system has been developed on Microsoft Visual Studio platform and C#, .net programming language has been preferred for system development. The developed systems have been simulated for execution time with varying query sequence length. Similarly, the speed up ratio has been estimated for varying sequence length. This is the matter of fact that the mathematical expressions and processing approaches causes the optimization in favor of diagonal sequencing approach and therefore the resulting consequences have also justified for the same. In the ascending sections the results and their analyzed significances have been discussed clearly in the respect of developed system model and its robustness in terms of various operational performance parameters.
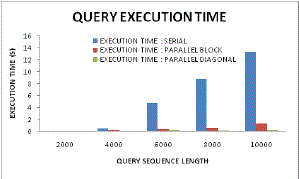image
Figure 13: Execution time analyses
Figure 13 illustrates the query execution time with varying sequence length. The relative performance among serial computation, parallel approach and diagonal scheme, it can be found here that with lower sequence length the diagonal sequencing approach is optimum and thus it illustrates negligible time taken for executing any query. On the other hand as per increase in sequence length it increases but as compared to serial sequencing and parallel approach still it is very meager amount. This happens because of the vectorized look up tables and metrics retrieval from dynamic programmable (DP) tables.
Figure 14 also advocates the same statements as in comparative graphs it can be found that as per increase in higher data counts or sequence length the diagonal sequence process and gene alignment has performed far better as compared to other approaches. In serial sequencing approach the execution time is comparatively higher as compared to parallel or proposed diagonal, this is because the serial processing has to suffer and estimate the DP tables in serial for all neighbouring matrices and thus the complete data estimation takes much time to accomplish overall sequencing. Even if this approach is employed with higher memory buffer the memory occupancy would be higher and thus the system would become bulky and hence cannot be an optimized solution for present needs.
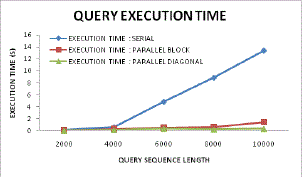image
Figure 14: Inclination of execution time for query analysis
Figure 15 and Figure 16 illustrates the speed up ratio in case of parallel block sequencing and parallel diagonal block sequencing approach. From these figures it can be found that for lower sequence length the speed up ratio approaches upto 96% in case of proposed parallel diagonal sequencing systems. Even with varying sequence length the speed up performance for proposed system is higher as compared to existing generic parallel sequencing.
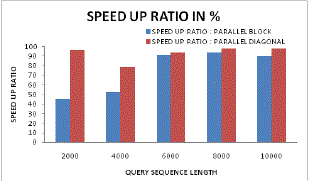image
Figure 15: Speed up ratio analysis for parallel Vs Diagonal parallel
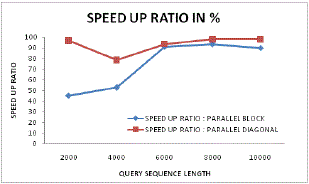image
Figure 16: Speed up ratio analysis
A dynamic and varying speed up analysis has been done in figure 16 where it can be found that the proposed system always follows up better initialization and continuation of speeding up even with higher sequence length. This is possible because of its novel DP parallel programming and data processing.
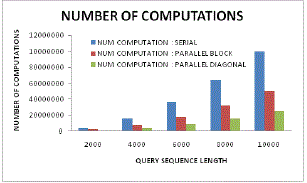image
Figure 17: Number of computation
Figure 17 illustrates the comparative analysis of number of computations and query sequence length for serial, parallel and proposed diagonal parallel sequencing or processing scheme. Here it can be visualized that in proposed system, there is the minimum need of computation even with higher sequence length. As compared to other traditional approaches, the proposed system has processed much lower computations as thus it signifies higher computation efficiency.
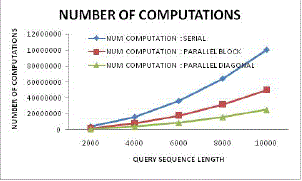image
Figure 18: Number of computation variation
Figure 18 illustrates the reduction in computational cost for parallel block based sequencing and proposed diagonal sequencing approach. Here from this figure it can be found that the proposed system has effectively reduced computation cost by the factor of more than 75% as compared to existing parallel block based processing scheme.

CONCLUSION AND FUTURE WORK
There has been a great significance of parallel computing and parallel programming paradigm in enhancing computational efficiency of various complicated systems such as genome sequencing, bulk data processing and gene alignment applications. This research work has been motivated from a goal to develop highly robust and optimized dynamic parallel programming approach that can come up with most efficient computational approach for biological gene sequencing. Considering the robustness of dynamic programming approaches here in this work, the author has proposed an optimization scheme for Smith Waterman (SW) algorithm enriched with Myers and Miller technique so as to come up with not only highly efficient computational approach but also a time and space optimization oriented system model. In this research work, author has developed a Diagonal Parallel Sequence Alignment Approach with Intra-task parallelization kernel. Here the author emphasizes its research on optimization of generic SW algorithm by means of enhancing trace backing efficiency, optimal mean estimation, forward and reverse approach of sequencing, diagonal gene sequencing with parallel alignment and enhanced pairwise sequence alignment. The consideration of Myers and Millers approach has made the system efficient by means of utilizing shared memory space and thus the associated dynamic programming lookup table makes the system functional without imposing much re-computation cost.
In this work, the predominant factors which has been optimized with its optimum possibility is Smith Waterman algorithm which functions in a unique Diagonal Parallel Alignment rather being in conventional serial or parallel sequencing approaches. The development of diagonal parallel sequencing makes the system efficient for estimating distance matrices and query matching with neighbour matrices that reduces overall computational count and thus the overall computational cost gets reduced. Similarly, on contrary of conventional serial and parallel sequencing the proposed approach has performed much better in terms of Query execution time; speed up ratio, number of computation, reduction in computational costs etc. The analysis of the retrieved comparative results of the proposed system along with conventional serial and parallel block sequencing approach, it has been found that the proposed system performs much better speed up ratio which approaches upto 96% irrespective of number of longer query sequence length. Among the three sequencing approaches the proposed system employs negligible time span for executing queries of varying length. Even serial and parallel approaches causes increase in query execution time as per increase in query length, but in contrary, the proposed diagonal parallel paradigm illustrates invariant and negligible execution time. Considering the number of computation and computational cost, it has been found that the proposed system reduces re-computation count to a great extent as compared to parallel and serial scheme. Serial block based sequencing approach increases the computational cost by intruding overheads in terms of re-computation to execute certain query length and the worst is in conventional approaches the computation cost increases as per increase in query length, which might be the most undesirable factor in case of gene sequencing which is a much long sequencing issue.
Considering overall performance matrices and time as well as space oriented computational optimization need, it can be stated that the proposed Diagonal Parallel Sequencing Approach has performed much better as compared to other serial and generic parallel sequencing paradigm. The developed system establishes itself as a potential candidate to be used for biological gene sequencing and parallel programming application requirements. Thus, the proposed research work is accomplished with its ultimate objectives, successfully. Although the proposed approach has illustrated much better as compared to other existing systems, but its realization with multi-core processors and certain optimized parallel processing algorithms might bring certain new hopes for further enhancements.

References
  1. F. Guinand, “Parallelism for computational molecular biology," in ISThmus 2000 Conference on Research and Development for the Information Society, Poznan, Poland, 2000.

  2. L. D'Antonio, “Incorporating bioinformatics in an algorithms course," in Proceedings of the 8th annual conference on Innovation and Technology in Computer Science Education, vol. 35 (3), 2003, pp. 211{214.

  3. H. B. J. Nicholas, D. W. D. II, and A. J. Ropelewski. (Revised 1998) Sequence analysis tutorials: A tutorial on search sequence databases and sequence scoring methods. [Online]. Available: http://www.nrbsc.org/old/education/tutorials/ sequence/db/index.html

  4. X. Huang, Chapter 3: Bio-Sequence Comparison and Alignment, ser. Current Topics in Computational Molecular Biology. Cambridge, MA: The MIT Press, 2002.

  5. S. Needleman and C. Wunch, “A general method applicable to the search for similarities in the amino acid sequences of two proteins," Journal of Molecular Biology, vol. 48, no. 3, pp. 443{453, 1970.

  6. T. F. Smith and M. S. Waterman, “Identification of common molecular subsequences," Journal of Molecular Biology, vol. 147, no. 1, pp.195{197, 1981.

  7. O. Gotoh, “An improved algorithm for matching biological sequences," Journal of Molecular Biology, vol. 162, no. 3, pp. 705-708, 1982.

  8. X. Huang and W. Miller, “A time-efficient linear-space local similarity algorithm," Adv.Appl.Math., vol. 12, no. 3, pp. 337{357, 1991.

  9. M. Camerson and H. Williams., “Comparing compressed sequences for faster nucleotide blast searches," IEEE/ACM Transactions on

  10. Computational Biology and Bioinformatics, vol. 4, no. 3, pp. 349{364, 2007.

  11. J. D. Frey, “The use of the smith-waterman algorithm in melodic song identification." Master's Thesis, Kent State University, 2008.

  12. J. Potter, J. W. Baker, S. Scott, A. Bansal, C. Leangsuksun, and C. Asthagiri, “Asc: an associative-computing paradigm," Computer, vol. 27, no.11, pp. 19{25, 1994.

  13. M. J. Quinn, Parallel Computing: Theory and Practice, 2nd ed. New York: McGraw-Hill, 1994.

  14. J. Baker. (2004) Simd and masc: Course notes from cs 6/73301: Parallel and distributed computing - power point slides. [Online]. Available: http://www.cs.kent.edu/wchantam/PDC Fall04/SIMD MASC.ppt

  15. Smith T, Waterman M: Identification of common molecular subsequences. J Mol Biol 1981, 147:195–197.

  16. Gotoh O: An improved algorithm for matching biological sequences. J Mol Biol 1982, 162:707–708.

  17. Thompson JD, Higgins DG, Gibson TJ: CLUSTALW: improving the sensitivity of progressive multiple sequence alignment through sequence weighting, position-specific gap penalties and weight matrix choice. Nucleic Acids Res 1994, 22:4673–4680.

  18. Liu Y, Schmidt B, Maskell DL: MSA-CUDA: Multiple Sequence Alignment on Graphics Processing Units with CUDA. 20th IEEE International Conference on Application-specific Systems, Architectures and Processors; 2009:121–128.

  19. Li H, Durbin R: Fast and accurate short read alignment with Burrows Wheeler transform. Bioinformatics 2009, 25(14):1755–1760.

  20. Liu Y, Schmidt B, Maskell DL: CUSHAW: a CUDA compatible short read aligner to large genomes based on the Burrows-Wheeler transform. Bioinformatics 2012, 28(14):1830–1837.

  21. Pearson WR, Lipman DJ: Improved tools for biological sequence comparison. Proc. Nat. Acad. Sci. USA 1988, 85(8):2444–2448.

  22. Altschul SF, Gish W, Miller W, Myers EW, Lipman DJ: Basical local alignment search tool. J Mol Biol 1990, 215(3):403–410.

  23. Altschul SF, Madden TL, Schaffer AA, Zhang J, Zhang Z, Miller W, Lipman DJ: Gapped BLAST and PSI-BLAST: a new generation of protein database search programs. Nucleic Acids Res 1997, 25(17):3389–3402.

  24. R.S. Harris, “Improved Pairwise Alignment of Genomic DNA,” PhD thesis, The Pennsylvania State Univ., 2007.

  25. S. Kurtz, A. Phillippy, A.L. Delcher, M. Smoot, M. Shumway, C. Antonescu, and S.L. Salzberg, “Versatile and Open Software for Comparing Large Genomes,” Genome Biology, vol. 5, no. 2, p. R12, 2004.

  26. S. Aluru, N. Futamura, and K. Mehrotra, “Parallel Biological Sequence Comparison Using Prefix Computations,” J. Parallel Distributed Computing, vol. 63, no. 3, pp. 264-272, 2003.

  27. S. Rajko and S. Aluru, “Space and Time Optimal Parallel Sequence Alignments,” IEEE Trans. Parallel Distributed Systems, vol. 15, no. 12, pp. 1070-1081, Dec. 2004.

  28. R.B. Batista, A. Boukerche, and A.C.M.A. de Melo, “A Parallel Strategy for Biological Sequence Alignment in Restricted Memory Space,” J. Parallel Distributed Computing, vol. 68, no. 4, pp. 548-561, 2008.

  29. C. Chen and B. Schmidt, “Computing Large-Scale Alignments on a Multi-Cluster,” Proc. IEEE Int’l Conf. Cluster Computing, pp. 3845, 2003.

  30. P. Zhang, G. Tan, and G.R. Gao, “Implementation of the SmithWaterman Algorithm on a Reconfigurable Supercomputing Platform,” Proc. First Int’l Workshop High-Performance Reconfigurable Computing Technology and Applications: Held in Conjunction with SC07 (HPRCTA ’07), pp. 39-48, 2007.

  31. X. Liu, L. Xu, P. Zhang, N. Sun, and X. Jiang, “A Reconfigurable Accelerator for Smith-Waterman Algorithm,” IEEE Trans. Circuits and Systems, vol. 54, no. 12, pp. 1077-1081, Dec. 2007.

  32. A. Boukerche, J.M. Correa, A.C.M.A. de Melo, R.P. Jacobi, and A.F. Rocha, “Reconfigurable Architecture for Biological Sequence Comparison in Reduced Memory Space,” Proc. IEEE Int’l Parallel and Distributed Processing Symp. (IPDPS), pp. 1-8, 2007.

  33. C. Chen and B. Schmidt, “An Adaptive Grid Implementation of DNA Sequence Alignment,” Future Generation Computer Systems, vol. 21, no. 7, pp. 988-1003, 2005.

  34. F. Sanchez, F. Cabarcas, A. Ramirez, and M. Valero, “Long DNA Sequence Comparison on Multicore Architectures,” Proc. 16th Int’l Euro-Par Conf. Parallel Processing (Euro-Par), pp. 247-259, 2010.

  35. A. Sarje and S. Aluru, “Parallel Genomic Alignments on the Cell Broadband Engine,” IEEE Trans. Parallel Distributed, vol. 20, no. 11, pp. 1600-1610, Nov. 2009.

  36. Driga, A.; Lu, P.; Schaeffer, Jonathan; Szafron, D.; Charter, K.; Parsons, I., "FastLSA: a fast, linear-space, parallel and sequential algorithm for sequence alignment," Parallel Processing, International Conference on 9-9 Oct. 2003, pp.48-57.

  37. Oliver, T.F.; Schmidt, B.; Maskell, D.L., "Reconfigurable architectures for bio-sequence database scanning on FPGAs," Circuits and Systems II: Express Briefs, IEEE Transactions on Dec. 2005, vol.52, no.12, pp.851-855.

  38. Hsien-Yu Liao; Meng-Lai Yin; Cheng, Y., "A parallel implementation of the Smith-Waterman algorithm for massive sequences searching," Engineering in Medicine and Biology Society,26th Annual International Conference of the IEEE , vol.2, pp.2817,2820, 1-5 Sept. 2004

  39. Arpit, G.; Adiga, R.; Varghese, K., "Space Efficient Diagonal Linear Space Sequence Alignment," BioInformatics and BioEngineering (BIBE), 2010 IEEE International Conference on , vol., no., pp.244,249, May 31 2010-June 3 2010

  40. Jha,S.; Kruger, L.; Shmatikov, V., "Towards Practical Privacy for Genomic Computation," Security and Privacy, 2008. SP 2008. IEEE Symposium on 18-22 May 2008, pp.216,230,

  41. Gardner-Stephen, P.; Knowles, G., "DASH: localizing dynamic programming for order of magnitude faster, accurate sequence alignment," Computational Systems Bioinformatics Conference, IEEE on 16-19 Aug. pp.732-735.

  42. Aji, A.M.; Wu-chun Feng, "Optimizing performance, cost, and sensitivity in pairwise sequence search on a cluster of PlayStations," BioInformatics and BioEngineering 8th IEEE International Conference on 8-10 Oct. 2008, pp.1-6.

  43. Popescu,M., "An ontological fuzzy Smith-Waterman with applications to patient retrieval in Electronic Medical Records," Fuzzy Systems (FUZZ), IEEE International Conference on 18-23 July 2010, pp.1-6.

  44. Rashid, N.A.A.; Abdullah, R.; Talib, A.Z.H.; Ali, Z., "Fast Dynamic Programming Based Sequence Alignment Algorithm," Distributed Frameworks for Multimedia Applications, 2006. The 2nd International Conference on , vol., no., pp.1,7, May 2006

  45. Changjin Hong; Tewfik, A.H., "Heuristic Reusable Dynamic Programming: Efficient Updates of Local Sequence Alignment," Computational Biology and Bioinformatics, IEEE/ACM Transactions on Oct.-Dec. 2009, vol.6, no.4, pp.570-582.

  46. Arslan A.N; "Multiple Sequence Alignment Containing a Sequence of Regular Expressions"; Computational Intelligence in Bioinformatics and Computational Biology, 2005. Proceedings of the IEEE Symposium on. 14-15 Nov. 2005, pp.1-7.

  47. Pulka, A.; Milik, A., "A new hardware algorithm for searching genome patterns," Signals and Electronic Systems, 2008.; International Conference on 14-17 Sept. 2008, pp.181-184.

  48. Shi-Yi Shen; Kui Wang; Gang Hu; Shu-Tao Xia; "On the Alignment Space and its applications," Information Theory Workshop on 22-26 Oct. 2006, vol., no., pp.165-169.

  49. Voss, G.; Muller-Wittig, W.; Schmidt, B., "Using Graphics Hardware to Accelerate Biological Sequence Database Scanning," TENCON 2005 2005 IEEE Region 10 , vol., no., pp.1,6, 21-24 Nov. 2005

  50. Harris, B.; Jacob, A.C.; Lancaster, J.M.; Buhler, J.; Chamberlain, R.D., "A Banded Smith-Waterman FPGA Accelerator for Mercury BLASTP," Field Programmable Logic and Applications, International Conference on 27-29 Aug. 2007, pp.765-769.

  51. Knowles, G.; Gardner-Stephen, P; "A new hardware architecture for genomic and proteomic sequence alignment," Computational Systems Bioinformatics Conference, 2004. CSB 2004. Proceedings. 2004 IEEE , vol., no., pp.730,731, 16-19 Aug. 2004

  52. Weiguo Liu; Schmidt, B.; Voss, G.; Schroder, A.; Muller-Wittig, W., "Bio-sequence database scanning on a GPU," Parallel and Distributed Processing Symposium on 25-29 April 2006, pp.8

  53. Alpern B.; Carter, L.; Kang Su Gatlin, "Micro-parallelism and High-Performance Protein Matching"; Supercomputing Proceedings of the IEEE/ACM SC95; pp.24-24.

  54. Zheng, Fang; Xu, Xianbin; Yang, Yuanhua; He, Shuibing; Zhang, Yuping, "Accelerating Biological Sequence Alignment Algorithm on GPU with CUDA," Computational and Information Sciences (ICCIS), International Conference on 21-23 Oct. 2011, pp.18-21.

  55. Das, S.; Dey, D., "A new algorithm for local alignment in DNA sequencing"; India Annual Conference; Proceedings of the IEEE INDICON on 20-22 Dec. 2004; pp.410-413.

  56. Junid, S.A.M.; Majid, Z.A.; Halim, A.K., "Development of DNA sequencing accelerator based on Smith Waterman algorithm with heuristic divide and conquer technique for FPGA implementation," Computer and Communication Engineering; International Conference on on 13-15 May 2008; pp.994-996.

  57. Boukerche, A.; Correa, J.M.; de Melo, A.C.M.A.; Jacobi, R.P.; Rocha, A.F., "Reconfigurable Architecture for Biological Sequence Comparison in Reduced Memory Space," Parallel and Distributed Processing Symposium, IPDPS 2007; IEEE International on 26-30 March 2007; pp.1-8.

  58. Delgado, G.; Aporntewan, C.; "Data dependency reduction in Dynamic Programming matrix," Computer Science and Software Engineering (JCSSE)Eighth International Joint Conference on 11-13 May 2011; pp.234-236.

  59. Riedel, D.E.; Venkatesh, S.; Wanquan Liu, “A Smith-Waterman Local Alignment Approach for Spatial Activity Recognition"; Video and Signal Based Surveillance, AVSS '06; IEEE International Conference on Nov. 2006; pp.54-54.

  60. Fa Zhang; Xiang-Zhen Qiao; Zhi-Yong Liu; "A parallel Smith-Waterman algorithm based on divide and conquer" Algorithms and Architectures for Parallel Processing Proceedings. Fifth International Conference on 23-25 Oct. 2002; pp.162-169.

  61. Sebastiao, N.; Dias, T.; Roma, N.; Flores, P., "Integrated accelerator architecture for DNA sequences alignment with enhanced traceback phase," High Performance Computing and Simulation (HPCS), 2010 International Conference on June 28 2010-July 2 2010; pp.16-23.

  62. Allred, J.; Coyne, J.; Lynch, W.; Natoli, V.; Grecco, J.; Morrissette, J., "Smith-Waterman implementation on a FSB-FPGA module using the Intel Accelerator Abstraction Layer," Parallel & Distributed Processing IPDPS in IEEE International Symposium on 23-29 May 2009; pp.1-4.

  63. Hasan,L.; Al-Ars, Z., "An efficient and high performance linear recursive variable expansion implementation of the smith-waterman algorithm," Engineering in Medicine and Biology Society, Annual International Conference of the IEEE3-6 Sept. 2009; pp.3845-3848.

  64. Razmyslovich, D.; Marcus, G.; Gipp, M.; Zapatka, M.; Szillus, A., "Implementation of Smith-Waterman Algorithm in OpenCL for GPUs," Parallel and Distributed Methods in Verification, 2010 Ninth International Workshop on, and High Performance Computational Systems Biology, Second International Workshop on Sept. 30 2010-Oct. 1 2010; pp.48-56.

  65. Cheng Ling; Benkrid, K.; Hamada, T; "A parameterizable and scalable Smith-Waterman algorithm implementation on CUDA-compatible GPU”; Application Specific Processors IEEE 7th Symposium on 27-28 July 2009; pp.94-100.

  66. Steinfadt, S.I., "SWAMP+: Enhanced Smith-Waterman Search for Parallel Models," Parallel Processing Workshops (ICPPW), 2012 41st International Conference on 10-13 Sept. 2012; pp.62-70.

  67. Nordin, M.; Rahman, A., "Utilizing MPJ Express Software in Parallel DNA Sequence Alignment," Future Computer and Communication, ICFCC 2009. International Conference on 3-5 April 2009; pp.567-571.

  68. Qian Zhang; Hong An; Gu Liu; Wenting Han; Ping Yao; Mu Xu; Xiaoqiang Li, "The optimization of parallel Smith-Waterman sequence alignment using on-chip memory of GPGPU," Bio-Inspired Computing: Theories and Applications (BIC-TA), 2010 IEEE Fifth International Conference on 23-26 Sept. 2010; pp.844-850.

  69. W. Liu; B. Schmidt; G. Voss; A. Schroder; W. Muller-Wittig; “Bio-Sequence Database Scanning on a GPU” Proc. 20th Int’l Conf. Parallel and Distributed Processing (IPDPS), 2006.

  70. Ali Khajeh-Saeed; Stephen Poole; J. Blair Perot; “Acceleration of the Smith–Waterman algorithm using single and multiple graphics processors”; Journal of Computational Physics, 229 (2010) 4247–4258.

  71. Sarje and S. Aluru, “Parallel Genomic Alignments on the Cell Broadband Engine,” IEEE Trans. Parallel Distributed, vol. 20, no. 11, pp. 1600- 1610, Nov. 2009.

  72. [71] Y. Liu, W. Huang, J. Johnson, and S. Vaidya, “GPU Accelerated Smith-Waterman,” Proc. Sixth Int’l Conf. Computational Science (ICCS), vol. 3994, pp. 188-195, 2006.

  73. Sheng-Ta Lee; Chun-Yuan Lin; Che Lun Hung; “GPU-Based Cloud Service for Smith-Waterman Algorithm Using Frequency Distance Filtration Scheme”; BioMed Research International Volume 2013 (2013), Article ID 721738, 8 pages.

  74. Sean O. Settle; “High-performance Dynamic Programming on FPGAs with OpenCL”; IEEE 2013.

  75. David Uliana; Krzysztof Kepa; Peter Athanas; “FPGA-based HPC application design for non-experts”; 2013 IEEE 24th International Conference on Application-Specific Systems, Architectures and Processors on June 05-June 07.

  76. Cehn, C.; Schmidt, B., "Computing large-scale alignments on a multi-cluster," Cluster Computing; Proceedings. 2003 IEEE International Conference on 1-4 Dec. 2003, pp.38-45.

  77. Batista, R.B.; Magalhaes Alves de Melo, Alba Cristina, "Z-align: An Exact and Parallel Strategy for Local Biological Sequence Alignment in User-Restricted Memory Space," Cluster Computing, 2006 IEEE International Conference on 25-28 Sept. 2006, pp.1-10.

  78. Rajko, S.; Aluru, S., "Space and time optimal parallel sequence alignments," Parallel and Distributed Systems, IEEE Transactions on Dec. 2004, vol.15, no.12, pp.1070-1081.

  79. Michael S. Farrar; “Optimizing Smith-Waterman for the Cell Broadband Engine. Gabor Ivan; Daniel Bank; Vince Grolmusz; “Fast and Exact Sequence Alignment with the Smith-Waterman Algorithm: The swissAlighn Webserver”; 7 Sep 2013.

  80. Yoshiki Yamaguchi; Hung Kuen Tsoi; Wayne Luk; “FPGA-based smith-waterman algorithm: analysis and novel design”; Proceeding ARC'11 Proceedings of the 7th international conference on Reconfigurable computing: architectures, tools and applications; Pages 181-192, 2011.

  81. A Surendar; M Arun; C Bagavathi; “EVOLUTION OF RECONFIGURABLE BASED ALGORITHMS FOR BIOINFORMATICS APPLICATIONS: AN INVESTIGATION”; International journal of life sciences, Biotechnology and Pharma Research; Vol. 2, No. 4, October 2013.

  82. Doug Hains; Zach Cashero; Mark Ottenberg;Wim Bohm; Sanjay Rajopadhye; “Improving CUDASW++, a Parallelization of Smith-Waterman for CUDA Enabled Devices.

  83. Michael Christopher Schatz; “HIGH PERFORMANCE COMPUTING FOR DNA SEQUENCE ALIGNMENT AND ASSEMBLY”; Thesis University of Maryland in 2010.

  84. Talal Bonny; M. Affan Zidan; Khaled N. Salama; “An Adaptive Hybrid Multiprocessor Technique for Bioinformatics Sequence Alignment”. Ligowski, L.; Rudnicki, W.; "An efficient implementation of Smith Waterman algorithm on GPU using CUDA, for massively parallel scanning of sequence databases," Parallel & Distributed Processing, 2009; IEEE International Symposium on 23-29 May 2009, pp.1-8.

  85. Mohd Nazrin Md Isa, “High Performance Reconfigurable Architectures for Biological Sequence Alignment”; Thesis; University of Edinburgh, March 2013.

  86. Brian Hang; Wai Yang; “A Parallel Implementation of Smith-Waterman Sequence Comparison Algorithm”; December 6, 2002.

  87. Jay Shendure; Hanlee Ji; “Next-generation DNA sequencing”; nature biotechnology volume 26 number 10; October 2008.

  88. Xiandong Meng; Chaudhary, V., "Exploiting Multi-level Parallelism for Homology Search using General Purpose Processors," Parallel and Distributed Systems, 2005. Proceedings. 11th International Conference on 22-22 July 2005; vol.2, pp.331,335,

  89. Zhihui Du; Zhaoming Yin; Bader, D.A., "A tile-based parallel Viterbi algorithm for biological sequence alignment on GPU with CUDA," Parallel & Distributed Processing, Workshops and Phd Forum (IPDPSW), 2010 IEEE International Symposium on 19-23 April 2010; pp.1-8.

  90. Shucai Xiao; Aji, A.M.; Wu-chun Feng, "On the Robust Mapping of Dynamic Programming onto a Graphics Processing Unit," Parallel and Distributed Systems (ICPADS), 2009 15th International Conference on 8-11 Dec. 2009; pp.26-33.

  91. Nawaz, Z.; Al-Ars, Z.; Bertels, K.; Shabbir, M., "Acceleration of Smith-Waterman using Recursive Variable Expansion," Digital System Design Architectures, Methods and Tools, 11th EUROMICRO Conference on 3-5 Sept. 2008, pp.915-922.

  92. Sadi, M.S.; Sami, A.Z.M.; Ahmed, I.U.; Ruhunnabi, A.; Das, N., "Bioinformatics: Implementation of a proposed upgraded Smith-Waterman algorithm for local alignment," Computational Intelligence in Bioinformatics and Computational Biology, IEEE Symposium on March 30 2009-April 2 2009; pp.87-91.

  93. Khairudin, N.; Mahmod, N.; Halim, A.K.A.; Junid, S. A M A; Idros, M. F M; Hassan, S. L M; Majid, Z.A., "Design and Analysis of High Performance Matrix Filling for DNA Sequence Alignment Accelerator Using ASIC Design Flow," Computer Modeling and Simulation (EMS),Fourth UKSim European Symposium on 17-19 Nov. 2010; pp.108-114.

  94. Gardner-Stephen, P.; Knowles, G., "DASH: localising dynamic programming for order of magnitude faster, accurate sequence alignment," Computational Systems Bioinformatics Conference Proceeding IEEE on 16-19 Aug. 2004; pp.732-735.

  95. Flynn and Laurie J.: Intel Halts Development of 2 New Microprocessors. The New York Times, 2004.

  96. Moore's Law to roll on for another decade, http://news.cnet.com/2100-1001984051.html. Retrieved 2012-2-10.

  97. Amdahl G.M.: The validity of the single processor approach to achieving large scale computing capabilities. In Proceedings of AFIPS Spring Joint Computer Conference, Atlantic City, N.J., AFIPS Press, pp.483–85.

  98. Gotoh O.: An improved algorithm for matching biological sequences. J Molecular Biology 1982, 162(3):705-708

  99. D.S. Hirschberg, “A Linear Space Algorithm for Computing Maximal Common Subsequences,” Comm. ACM, vol. 18, no. 6, pp. 341-343, 1975.

  100. O. Gotoh, “An Improved Algorithm for Matching Biological Sequences,” J. Molecular Biology, vol. 162, no. 3, pp. 705-708, Dec. 1982.

  101. Saitou M. and Nei N.: The neighbor-joining method: a new method for reconstructing phylogenetic trees. Mol. Biol. Evol, 1987, 4:406-425.