This paper presents the process of removal of impulse noises using different median filters. This contains a vector median filter that includes a new mechanism for the detection of impulses in colour images prior to further processing operations. When compared to other filters, the proposed filter will be tested for images corrupted by two sided fixed impulse noise model, nothing but salt and pepper noise. If the central vector pixel in a kernel is found to be corrupted, it is replaced by the vector median of the kernel, else it is kept unchanged. The vector pixels in a specified window are ranked on the basis of sum of the distances between each vector pixel and the other vector pixels in the window. Since the detection mechanism uses absolute deviation values, the computational complexity is reduced. The results show a better performance of the proposed algorithm in lesser execution time as compared to a number of existing schemes for restoring colour images corrupted by impulse noise.
Keywords |
| kernel; vector median filter; rank-conditioned vector median filter; rank-conditioned and threshold vector
median filter; centre-weighted vector median filter; two-sided fixed impulses noise model. |
INTRODUCTION |
| Order statistic filters [1] exhibit excellent robustness properties in the presence of impulse noise. An image is often
corrupted by on-off impulse noise of relatively short duration. The impulse is caused by a variety of sources, such as
switching, adverse channel environment in a communication system, noise in electronic sensors of the data acquisition
system etc. Suppression of impulse noise is an important image processing task. Median filter is an example of an order
statistics filter which exhibits superior noise reduction capabilities, with considerably less blurring compared to linear
filters. The median is widely used in statistics and was introduced by Tukey in time series analysis [2], [3]. In median
filtering, the values of the pixels in a kernel are first sorted, and then the median value is used to replace the central
pixel. Median filters are used for gray scale images. |
| In multichannel signals, each sample is a vector with multiple components. An example of a multiple channel
signal is a color image. As per the RGB model [4] of color images, every vector pixel in a color image has three
components. The ordering of the vector pixel data is carried out by considering a suitable distance measure. The vector
pixels, in a kernel, are ordered depending on the sum of the distances between each vector pixel and the other vector
pixels in a window or kernel. |
RELATED WORK |
| The vector pixel with the smallest sum of distances form`s the vector median. Since authors used a vector
median filter that tends to alter all the pixels in an image irrespective of whether they were corrupted by noise, the
restored image suffers from blurred and distorted features. That is why the modifications of vector median filter
incorporate an impulse noise detection mechanism so as to preserve image details and selectively remove the noise. In
this paper, an alternative algorithm, which does not require the ranking calculation and ordering of the vector pixels for
the purpose of impulse detection, has been proposed. The objective is to use first order statistics on the difference
values of the red and green intensities and the green and blue intensities of each vector in a kernel. The arithmetic mean
of these difference values for vectors surrounding the central pixel is taken. If the absolute deviation of the central
vector in a kernel, from the mean of difference values is greater than the arithmetic mean of the absolute deviation
values of the vectors that surround the central vector pixel, then central vector pixel is considered to be corrupted. Since distance calculation and ordering is not required, this process provides a quick decision as to whether a pixel is
corrupted or not. If a pixel is found to be corrupt, only then is the normal vector median filtering process resorted to. |
| The rest of the paper is organized as follows. An impulse noise model is explained in section II. The vector
median filter, rank conditioned vector median filter, rank-conditioning and threshold vector median filter, centreweighted
vector median filter and the proposed filter are formulated in section III. In section IV the experimental
results are provided. Conclusion and future direction of work is presented in section V. |
IMPULSE NOISE MODEL |
| The two sided fixed impulses model is also called the “salt and pepper noise model”. Impulse noise may either have
very large value called the ’salt’ noise or a very small value called the ’pepper’ noise. Let it be considered that ’p’ gives
the probability that a very low value error occurs at a signal component and that ’q’ gives the probability that a very
high value error occurs at a signal component. Then the probability that error occurs in any signal component is given
by (p+q). If B is the number of bits used per pixel component then (2B-1) or ’h’ represents the ’salt’ noise, while 0 or ’l’
represents the ’pepper’ noise. |
| Let XC, (where c = 1 for red, 2 for green or 3 for blue) be a pixel component of a vector pixel X in any one of the
channels of a multichannel image. The model may be expressed in the following way: |
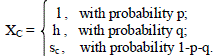 (1) (1) |
| Where sc is a noise free pixel component. |
FORMULATION |
| A 3 × 3 kernel is considered for all the following filters since it allows faster convergence of the filter [10]. The
kernel has 9 vector pixels. They are represented as Xi where i = 1, 2,. . ., 9. A top to bottom, left to right numbering is
carried out for the pixels. Thus X1 is the upper left vector, X5 is the central vector and X9 is the bottom right vector. This
scheme is chosen for simplicity of representation. In a window the vector pixels are |
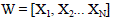 (2) (2) |
| Where N=9. Each vector pixel has three components as per the RGB colour model |
A. THE VECTOR MEDIAN FILTER (VMF): |
| In the vector median filter [5]-[8] for the ordering of the vectors in a particular kernel or mask a suitable distance
measure is chosen. The vector pixels in the window are ordered on the basis of the sum of the distances between each
vector pixel and the other vector pixels in the window. The sum of the distances is arranged in the ascending order and
then the same ordering is associated with the vector pixels. The vector pixel with the smallest sum of distances is the
vector median pixel. The vector median filter is represented as |
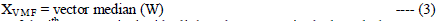 |
| If δi is the sum of the distances of the ith vector pixel with all the other vectors in the kernel, then |
 |
| Where (1 ≤ i≤ N) and Xi, Xj are the vectors, N=9. Δ(Xi,Xj), is the distance measure given by the L1 normal to the
city block distance which is more suited to non correlated noise [5]. The ordering may be illustrated as |
 |
 |
| Where the subscripts are the ranks. Since the vector pixel with the smallest sum of distances is the vector median
pixel, it will correspond to rank 1 of the ordered pixels, i.e. |
 |
THE RANK-CONDITIONED VECTOR MEDIAN FILTER (RCVMF): |
| The rank conditioned vector median filter [5], [10] improves the performance of the vector median filter. The vector
median of the kernel replaces the central pixel when the rank of the central vector pixel is greater than a predefined
rank of a healthy vector pixel inside the window. To find out the rank of the healthy vector pixel the code simulating
RCVMF is executed on a noiseless image. Then, the mean value of the obtained ranks of the central vector pixel is
calculated. This value is then rounded-off to a whole number, and in this paper it is considered to be the rank of the
healthy vector pixel of a kernel. Then this rank is used for simulations at various noise percentages. |
| The rank conditioned vector median filter can be expressed as: |
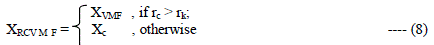 |
| Where rc is the rank of the central vector pixel and c = 5. And rk is the predefined healthy vector pixel rank
inside the window. |
| Image details are preserved better if the rank chosen is large. However this is at the cost of passing more impulses
in the vector median output. On the other hand, impulses are removed to the maximum extent with a smaller value of
the rank but blurring effect is more pronounced in the restored image. |
THE RANK-CONDITIONING AND THRESHOLD VECTOR MEDIAN FILTER (RCTVMF): |
| The rank-conditioning and threshold vector median filter [5], aims to further enhance the RCVMF by
incorporating an additional test - a distance threshold for the detection of impulses. In RCVMF a central vector having
a rank greater than the predefined rank implies a corrupt vector. However, it may not be true always, because the
vectors may be close as per the distance measure. Hence, another criterion θ , is taken into account. It is the distance
between the central vector pixel and the vector pixel corresponding to the predefined rank. To find out the value of this
pre-determined distance threshold θ, the code simulating RCTVMF is executed on a noiseless image. Then the mean of
the obtained θ values is calculated and used for the simulations at various noise percentages. This value is used in the
program to help select only the corrupt central vector pixels. |
| The distance D is calculated as follows: |
 |
| Where Xc is the central vector and X(k) (1< k <9) is a rank ordered and healthy vector pixel inside the
window. On the basis of the above formulation, the filter has following form: |
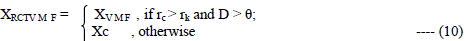 |
| The distance D is normally very big if impulses are present at the center of the window. If the value of the
threshold is reduced, more and more number of the central vector pixels will be replaced by the vector median and this
filter will resemble the RCVMF. |
THE CENTRE WEIGHTED VECTOR MEDIAN FILTER (CWVMF): |
| In the case of the center weighted median filter [10]-[11] the kernel vector pixels are assigned some nonnegative
values called weights. The center vector pixel is assigned a non negative weight while the weight of the
neighboring pixels is kept unity. The weights denote the number of copies of a vector pixel that are to be used. Then the vector median of the vector pixels and their copies is obtained. The output Y (say), of a weighted median filter of span
N (where N generally denotes the kernel size, N = 9) associated with N integer weights, |
 |
| Is given by, |
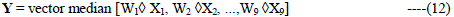 |
| Where vector median [.] denotes the vector median operation and ◊ denotes duplication, i.e., |
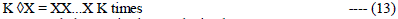 |
| The center weight is kept odd so that a central element is always obtained. |
| If the center weight has value of one then the present filter becomes a vector median filter. If the center weight is
given a value greater that the kernel size then the filter performs as an identity filter. Larger central vector weights
imply superior detail preservation and inferior noise removal capability as compared to smaller central vector weights.
The simulation of the CWVMF has been carried out considering the center weight to be 3 and the weights of the
neighboring pixels to be 1 through all the evaluations. |
THE PROPOSED FILTER (PF) |
| In the proposed filter i.e Absolute Deviation Filter the impulse noise detection mechanism does not require the
distance calculation and subsequent ordering of the vectors of a kernel. |
| The algorithm deals with the difference values of the red (R) and the green (G) intensities denoted by ΩRGi (say), and
the difference values of the green (G) and blue (B) intensities denoted by ΩGBi (say), (where 1 ≤ i≤ N, N=9). |
| In a 3 × 3 kernel, it has been observed empirically that ΩRGi and ΩGBi values closely correspond to each other. Thus
the mean absolute deviation D’RG and D’GB i.e. the mean of DRGj and DGBj (where 1 ≤ j ≤ N, and j ≠ c, c = (N+1)/2, N =
9) has small values. DRGj and DGBj are the absolute deviation [15] values of ΩRGj and ΩGBj from Ω'RG and Ω'GB
respectively. Ω'RG and Ω'GB denote the mean of ΩRGj and ΩGBj (where 1 ≤ j ≤ N, and j ≠ c, c = (N+1)/2, N = 9 ). |
| The absolute deviation of the central vector ΩRGc and ΩGBc values from Ω'RG and Ω'GB is obtained respectively as
DRGc and DGBc. |
| If the absolute deviation DRGc or DGBc of the central vector pixel exceeds the value of D’RG or D’GB respectively for a
3 × 3 kernel, the central vector pixel is to be replaced. The central vector pixel is replaced by the vector median of the
kernel. The algorithm may be represented as follows. |
| The required values: |
 |
 |
| where i = [1,2,. . .,N], N = 9, kernel size 3 × 3, and R,G,B are the red, green and blue components. The mean of
ΩRGj and ΩGBj (where 1 ≤ j ≤ N, and j ≠c, c = (N+1)/2, N =9) |
 |
 |
| D is the absolute deviation & E is the expectation operator. |
 |
 |
| Where i = [1, 2,. . .,N], N = 9. The symbol |.| indicate the absolute value. |
| The mean of DRGj and DGBj (where 1 ≤ j ≤ N, and j ≠ c, c = (N+1)/2, N = 9) are |
 |
 |
| Now |
 |
 |
| Where ‘c’ denotes central vector. |
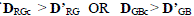 |
| Central vector corrupted, hence |
| Central vector replaced by vector median of kernel ---- (24) |
| In the proposed algorithm the process of VMF, specifically the distance calculation and subsequent ordering of
the vector pixels is done only when a particular vector pixel is found corrupt. However for the other variants of VMF,
distance calculation and ordering of the vector pixels is carried out for all the image vectors. |
EXPERIMENTAL RESULTS |
| The test images used are Lena, Mandrill, Miramar, Aero plane, Lake and Tulips. Each vector pixel is of 24 bits,
with 8 bits for every channel. The size of all the images is 512×512. Two-sided fixed impulses noise model has been
used for evaluation. Impulse noises are artificially injected in these images. The performances are judged by the visual
observation and in terms of the peak signal to noise ratio (PSNR). The PSNR value for the color images is given by: |
 |
| Where IMAX is the maximum pixel value of the component of the vector pixel of the original image. MSE
represents the mean square error [11] between the original image and the filtered image, which is given by: |
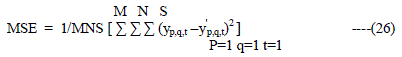 |
| Where S, M and N are the number of channels, length and width of the image (S = 3, for color images)
respectively. The values Yp, q, t and Y 'p,q,t are the components of the original and filtered vector pixels respectively. In
all cases, a window of 3 × 3 size is used which is made to slide over the image vector pixels. |
| An image is corrupted by impulse noise generated as per the two sided fixed impulses model. The corruption is
carried out at different noise percentages and the proposed filter is tested using these increasingly corrupted images.
The filters used for comparison are the vector median filter (VMF), the center weighted vector median filter
(CWVMF), and the rank conditioned vector median filter (RCVMF) and the rank-conditioning and threshold vector
median filter (RCTVMF). |
| Table I lists the performance of the various filters in removal of impulse noise from various images corrupted with 20%
(i.e. 6.67% per channel) impulse noise generated according to two sided fixed impulses noise model. The PSNR values
highlight the better performance of the proposed filter. |
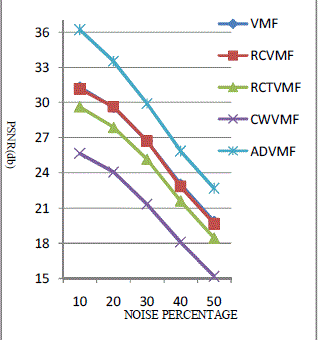
| Observations are made using a River image and the graphs are plotted in Fig. 1 where the noise percentages range
from 0% to 60% (i.e. 20% per channel). It is clear from the graph in Fig. 1 that the proposed filter provides improved
results as compared to the other filters that have been mentioned in this paper, while de-noising pictures corrupted by noise in the above mentioned range. The improved performance, in terms of PSNR, is observed up to a corruption of
about 36% (i.e. 12 % per channel). |
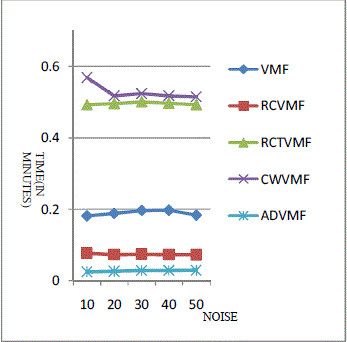
| A comparative study of the time taken by the proposed filter in removal of impulse noises generated by two-sided
fixed impulses model, at different noise percentages, is carried out. The observations are made using a Miramar image
and the graphs are plotted in Fig. 2 where the noise percentages range from 0% to 60% (i.e. 20% per channel). It is
clear from the graph in Fig. 2 that the proposed filter takes lesser processing time than the other filters that have been
mentioned in this paper, while de-noising pictures containing impulses ranging from 0% to 60% (i.e.20% per channel).
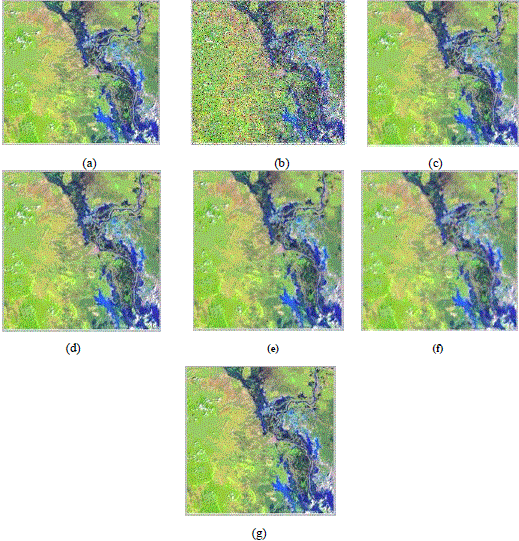
The Fig. 3 shows the original image, corrupted image and filtered images using different types of vector median filters
and proposed filter. The subjective results show that the proposed filter can retain more detailed information in the
filtered image. |
CONCLUSION |
| This work presents a vector median filter which is capable of detecting impulses from colour images prior to
filtering. From the experimental results and visual observation it has been seen that the performance of the proposed
filter is better for removal of impulse noises generated by two-sided fixed impulses noise model at low noise
percentages per channel. It is due to the ability of the detection mechanism of the proposed filter to detect the corrupted
pixels rightly. Moreover, limiting the distance calculation and ranking process to only the kernel centred on the
corrupted pixels, rather than for all the pixels, has considerably lowered the processing time of the proposed filter.
From the experimental results it has been found that the proposed filter takes lesser time for processing a noised image.
For low noise levels, specifically below 10% (i.e. 3.33% per channel), the proposed filter requires approximately half
the processing time of the existing filters. Moreover, the proposed scheme gives a stable performance over a wide
variety of images. |
| Further performance analysis of the proposed algorithm may be carried out for other noise models like bit error
model and colour impulses noise model [5]. |
Tables at a glance |
 |
| Table 1 |
|
Figures at a glance |
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
|
References |
- I. Pitas and A. N. Venetsanopoulos, ?Order Statistics in Digital Image Processing,? Proc. of IEEE, vol. 80, no. 12, pp. 1893-1921, December 1992.
- J. W. Tukey, ?Nonlinear (nonsuperposable) methods for smoothing data,? Congr. Res. EASCON record, pp. 673, 1974.
- J. W. Tukey, Exploratory data analysis, Addison-Wesley, Mento Park, 1977.
- R. C. Gonzalez and R. E. Woods, Digital image Processing, 2nd edition, Pearson Education (Singapore) Pte. Ltd., Indian Branch, 482 F.I.E. Patparganj, Delhi, 2002.
- J. Astola, P. Haavisto and Y. Neuvo, ?Vector Median Filters,? Proc. Of IEEE, vol. 78, no. 4, pp. 678-689, April 1990.
- A. J. Bardos and S. J. Sangwine, ?Selective Vector Median Filtering of Colour Image,? Proc. of Sixth Int. Conf. on Image Processing and its Applications, vol. 2, no. 443, pp. 708-711, July 1997.
- M. I. Vardavoulia, I. Andreadis and P. Tsalides, ?A New Vector Median Filter for Colour Image Processing,? Pattern Recognition Letters, Elsevier Science Inc., NY, vol. 22, no. 6-7, pp. 675-689, 2001.
- L. Alparone, S. Baronti and R. Carla, ?Express Letters - Two- Dimensional Rank-Conditioned Median Filter,? IEEE Trans. on Circuits and Systems-II: Analog and Digital Signal Processing, vol. 42, no. 2, pp. 130-132 , February 1995.
- K. M. Singh and P. K. Bora, ?Adaptive Vector Median Filter for Removal Impulses from Color Images,? Proc. of Int. Symposium on Circuits and Systems, vol. 2, pp. II-396 - II-399, May 2003.
- L. Yin, R.Yang, M. Gabbouj and Y. Neuvo, ?Circuits and Systems Exposition - Weighted Median Filters: A Tutorial,? IEEE Trans. On Circuits and Systems - II: Analog and Digital Signal Processing, vol. 43, no. 3, pp. 157-192, March 1996.
- M. Muneyasu, N. Nishi and T. Hinamoto, ?Brief Communication ? A New Adaptive Center Weighted Median Filter Using Counter Propagation Networks,? Journal of the Franklin Institute, pp. 631-639, March 2000.
|