International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Menu

ISSN ONLINE(2320-9801) PRINT (2320-9798)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Performance Analysis of Classifiers to Effieciently Predict Genetic Disorders Using Gene Data

R Preethi1, G M SuriyaaKumar1, N G Bhuvaneswari Amma2, G Annapoorani3
  1. PG Scholar, Database Systems, Indian Institute of Information Technology, Srirangam, India
  2. Faculty, Department of Information Technology, Indian Institute of Information Technology, Srirangam, India
  3. Assistant Professor, Department of Computer Science and Engineering, University College of Engineering, BIT Campus, Tiruchirappalli, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Abstract

In this paper, we study the performance of various classifier models for predicting disease classes using genetic microarray data. We analyze the best from among the four classifier methods namely Naïve Bayes, J48, IB1 and IBk. Classification is a technique to predict the best classifier. Classification is used to classify the item according to the features of the item with respect to the predefined set of classes. Naive Bayes algorithm is based on probability and j48 algorithm is based on decision tree. In this paper, we classify the dataset using classes and we found the J48 classifier performs better in accurately predicting the disease classes.





Keywords
Prediction, Naive Bayes, J48, IB1, IBk.

INTRODUCTION
Data mining is growing in various applications widely like analysis of organic compounds, medicals diagnosis, product design, targeted marketing, financial forecasting, automatic abstraction, predicting shares of television audiences etc. Data mining refers to the analysis of the large quantities of data that are stored in computers. Data mining is not specific to one type of media or data [1]. Data mining should be applicable to any kind of information repository. Data mining is being put into use and studied for databases, including relational databases, object-relational databases and object oriented databases, data warehouses, transactional databases, unstructured and semi-structured repositories such as the World Wide Web, advanced databases such as spatial databases, multimedia databases, time-series databases and textual databases, and even flat files[2].
Classification analysis is the organization of data in given classes. Also known as supervised classification, the classification uses given class labels to order the objects in the data collection.Classification approaches normally use a training set where all objects are already associated with known class labels [3]. The classification algorithm learns from the training set and builds a model. The model is used to classify new objects. Classification is a statistical operation in which certain objects are put into groups or classes according to their characteristics, sometimes called attributes, found on a training set. There are many approaches to classification in literature, like Decision trees, neural networks, Support vector machines and Bayesian networks, among others.From the aforementioned classifying methods, the Bayesian approach is the most commonly used to deal with uncertainty, because it is based on the probability theory.

RELATED WORK

Naive Bayes classifier
A well-known classifier is the Naive Bayes classifier, a simple type of Bayesian network that explodes the conditional independence assumption among attributes given the class. In real life, this assumption does not hold most of the time. However, Naive Bayes classifiers have proven to be successful.Generally, in a Naive Bayes classifier the attributes are discrete, but in most real-life situations, attributes are continuous [4].The naive Bayes classifier greatly simplifies learning by assuming that features are independent given class. Although independence is generally a poor assumption, in practice naive Bayes often competes well with more sophisticated classifiers. Our broad goal is to understand the data characteristics which affect the performance of naive Bayes.

Decision tree algorithm J48:
J48 classifier is a simple C4.5 decision tree for classification. It creates a binary tree. The decision tree approach is most useful in classification problem. With this technique, a tree is constructed to model the classification process. Once the tree is built, it is applied to each tuple in the database and results in classification for that tuple.

Algorithm J48:
image
While building a tree, J48 ignores the missing values i.e. the value for that item can be predicted based on what is known about the attribute values for the other records. The basic idea is to divide the data into range based on the attribute values for that item that are found in the training sample [5]. J48 allows classification via either decision trees or rules generated from them.

IB1 Classifier
IB1 classifier uses a simple distance measure to find the training instance closest to the given test instance, and predicts the same class as this training instance. If multiple instances are the same (smallest) distance to the test instance,the first one found is used. The IB1 algorithm, is the simplest instance-based learning classification method [13]. IBL algorithms are derived from the nearest neighbour pattern classifier (Cover & Hart, 1967). They are highly similar to edited nearest neighbour algorithms (Hart, 1968; Gates,1972; Dasarathy, 1980), which also save and use only selected instances to generate classification predictions. While several researchers demonstrated that edited nearest neighbour algorithms can reduce storage requirements with, at most, small losses in classification accuracy, they were unable to predict the expected savings in storage requirements. IBL algorithms are instead incremental and their goals include maximizing classification accuracy on subsequently presented instances [6]. The similarity and classification functions determine how the set of saved instances in the concept description are used to predict values for the category attribute. Therefore, IBL concept descriptions not only contain a set of instances, but also include these two functions.
In IB1 method, the similarity function used here is:
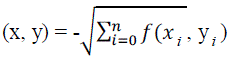image
Where the instances are described by n attributes. We define f(xi yi;) = (xi,- yi)2 for numeric-valued attributes and f(xi, yi) = (xi ≠ yj) for Boolean and symbolic-valued attributes. Missing attribute values are assumed to be maximally different from the value present. If they are both missing, then f(xi, yi) yields 1. IB1 is identical to the nearest neighbour algorithm except that it normalizes its attributes' ranges, processes instances incrementally, and has a simple policy for tolerating missing values.

IBK (K - Nearest Neighbour)
IBK is a k-nearest-neighbour classifier that uses the same distance metric. The number of nearest neighbours can be specified explicitly in the object editor or determined automatically using leave-one-out cross-validation focus to an upper limit given by the specified value. IBK is a knearest- neighbour classifier. A kind of different search algorithms can be used to speed up the task of finding the nearest neighbours. A linear search is the default but further options include KD-trees, ball trees, and so-called “cover trees”. The distance function used is a parameter of the search method. The remaining thing is the same as for IBL—that is, the Euclidean distance; other options include Chebyshev, Manhattan, and Minkowski distances. Predictions from more than one neighbour can be weighted according to their distance from the test instance and two different formulas are implemented for converting the distance into a weight.

CRITERIA USED FOR COMPARISON EVALUATION

Accuracy Classification
All classification result could have an error rate and it may fail to classify correctly. So accuracy can be calculated as follows.
Accuracy = (Instances Correctly Classified / Total Number of Instances)*100 %(2)

Mean Absolute Error
MAE is the average of difference between predicted and actual value in all test cases. The formula for calculating MAE is given in equation shown below:
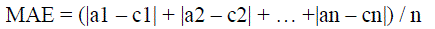image
Here ‘a’ is the actual output and ‘c’ is the expected output.

Root Mean Squared Error
RMSE is used to measure differences between values predicted by a model and the values actually observed. It is calculated by taking the square root of the mean square error as shown in equation given below:
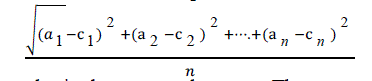image
Here ‘a’ is the actual output and c is the expected output. The mean-squared error is the commonly used measure for numeric prediction.

Confusion Matrix
A confusion matrix contains information about actual and predicted classifications done by a classification system. The classification accuracy, mean absolute error, root mean squared error and confusion matrices are calculated for each machine learning algorithm using the machine learning tool.
The tables presented above, represent the various accuracy measures for various classifier models used to predict the disease using the gene data. The best classifier model is found out using the various criteria used for evaluation. The criteria used for evaluation include mean absolute error, root mean squared error, relative absolute error and root relative square error.
The tables presented above, represent the various accuracy measures for various classifier models used to predict the disease using the gene data. The best classifier model is found out using the various criteria used for evaluation. The criteria used for evaluation include mean absolute error, root mean squared error, relative absolute error and root relative square error.
The Figures 1 and 2 illustrate the various statistics of classifiers. Figure 1 represents the correctly and incorrectly classified instances for all classifiers. Figure 2 illustrates the accuracy measures for all classes in Naïve Bayes Classifier.Figure 2 and Figure 3 represents the accuracy measures of different classes. The gene data has been classified with accordance to five classes. The five classes describe five types of heredity disorder. Thus using these predictions one can easily identify for one gene pattern, the occurrence of heredity disorder.The figure 4 represents the accuracy measure of the data using IB1 classifier. From the graph the disorder class MED is found to be classified with more errors. Comparatively the other classes have less error compared to MED class disorder.
Figure 5 and 6 represent the accuracy measure for IBk classifier and Roc curve for a class. From all the conclusions it is clear that j48 classifier performs better than other classifiers. May be the experimental results could vary from dataset to dataset depending upon the attributes and instances.

CONCLUSION AND FUTURE WORK
Data mining can be defined as the extraction of usefulknowledge from large data repositories. In this paper, theclassification algorithms namely Naïve Bayes, J48, IB1 and IBk classifiers are used for classifying gene data in order to predict heredity disorders. Byanalysing the experimental results it is observed that the J48 classifier yields better result than other classifier. As development of this paper, we would try obtain better results based upon iterating the training set data. How far does the accuracy increases as the training data increases.

Tables at a glance
Table icon Table icon Table icon Table icon Table icon
Table 1 Table 2 Table 3 Table 4 Table 5

Figures at a glance
Figure 1 Figure 2 Figure 3
Figure 1 Figure 2 Figure 3
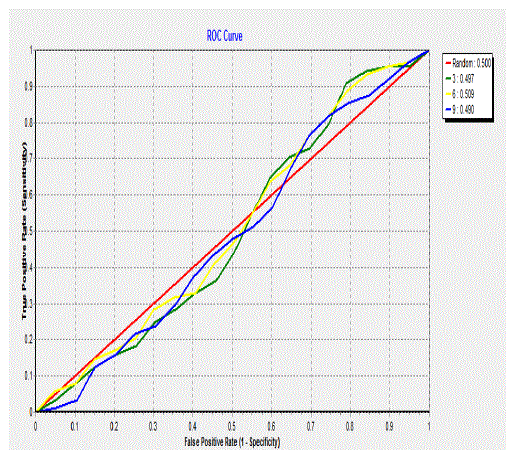Figure 4 Figure 5 Figure 6
Figure 4 Figure 5 Figure 6

References