Keywords
|
| Image deconvolution, alternating direction method of multipliers (ADMM), boundary conditions, periodic deconvolution, in painting, frames |
INTRODUCTION
|
| Deconvolution is an inverse problem where the observed image is modeled as resulting from the convolution with a blurring filter, possibly followed by noise, and the goal is to estimate both the underlying image and the blurring filter.In deconvolution , the pixels located near the boundary of the observed image depend on pixels (of the unknown image) located outside of its domain. The typical way to formalize this issue is to adopt a so-called boundary condition (BC). |
| ? The periodic BC refers to the image repeats in all directions. Its matrix representation can be implemented via the FFT. |
| ? The zero BC assumes a black boundary, so that pixels outside the boarders of the image have zero value, thus the matrix representing the convolution is block-Toeplitz, with Toeplitz blocks. |
| ? Inreflexive and anti-reflexive BCs, the pixels outside the image domain are a mirror image of those near the boundary, using even or odd symmetry, respectively. |
| For the sake of simplicity and computational convenience, most fast deconvolution algorithms assume periodic BC, which has the advantage of allowing convolutions to be efficiently carried out using the FFT. However, as illustrated in Fig. 1, these BC are notaccurate and are quite unnatural models of most imaging systems. Deconvolution algorithms that ignore this mismatch and wrongly assume periodic BC lead to the well known boundaryartifacts. A better assumption about the image boundaries is simply they are unobserved/unknown,which models well a canonical imaging system where an image sensor captures the cental part of the image projected by the lens.The assumptions(unnatural) of periodic boundary conditions as illustrated in Fig 1. |
| In quadratic regularization, image deconvolution with periodic BC corresponds to a linear system, wherethe corresponding matrix can be efficiently inverted in the DFTdomain using the FFT.The technique to deconvolutionunder frame-based analysisnon-smooth regularization; that work proposes an algorithmbased on variable splitting and quadratic penalization, using the method to solve the linear system at each iteration.That method is related to, but it is not ADMM, thus has no guarantees of converge to a minimizer of the original objective function. Although mentions the possibility of using the method within ADMM, that option was not explored. |
| The image deconvolution under frame based analysis non-smooth regularization using ADMM inherit all the desirable properties of previous ADMM-based deconvolution methods: all the update equations (includingthe matrix inversion) can be computed efficiently without using inner iterations; convergence is formally guaranteed. |
RELATED WORK
|
Iterative Shrinkage Thresholding algorithm:
|
| Consider common form of algorithms for linear inverse problems in imaging, |
 |
| Where A=BW, B is the matrix representation of the direct operator, i.e., x = W??, where ?? ∈ ??? , and the columns of the ?? × ??matrix W are the elementsof a wavelet1 frame. |
Arguably, the standard algorithm for solving problems of the form (1) is the so-called iterative shrinkage/thresholding (IST)algorithm. IST can be derived as an expectation-maximization (EM) algorithm, as a majorization-minimization (MM) method, or as a forward-backward splitting technique. A key ingredient of IST algorithms isthe so-called shrinkage/thresholding function, also known as the Moreau proximal mapping or the denoising function, associated to the regularizer, which provides the solutionof the corresponding pure denoising problem. Formally, thisfunction is denoted as 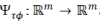 and defined as and defined as |
 |
| IST may be quite slow, specially when ?? is very small and/or the matrix A is very ill-conditioned. This observation has stimulated work on faster variants of IST, which we will briefly review in the next paragraphs. |
Two-step IST (TwIST):
|
| In the two-step IST (TwIST) algorithm [1], each iterate depends on the two previous iterates, rather than only on the previous one (as in IST). This algorithm may be seen as a non-linear version of the so-called two-step methods for linear problems [2]. TwIST was shown to be considerably faster than IST on a variety of wavelet-based and TV-based image restoration problems; the speed gains can reach up to two orders of magnitude in typical benchmark problems. |
Fast IST (FISTA):
|
| Another two-step variant of IST, named fast IST algorithm (FISTA), was recently proposed and also shown to clearly outperform IST in terms of speed. FISTA is a non-smooth variant of Nesterov’s optimal gradient-based algorithm for smooth convex problems. |
Standing for sparse reconstruction by seperable approximation (SpaRSA):
|
A strategy recently proposed to obtain faster variants ofIST consists in relaxing the condition 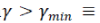 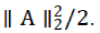 Inthe SpaRSA (standing for sparse reconstruction by separableapproximation) framework, a different γt is used ineach iteration (which may be smaller than γmin , meaning largerstep sizes). It clearly outperforms standard IST and a convergence result for SpaRSA. Inthe SpaRSA (standing for sparse reconstruction by separableapproximation) framework, a different γt is used ineach iteration (which may be smaller than γmin , meaning largerstep sizes). It clearly outperforms standard IST and a convergence result for SpaRSA. |
| Finally, when the slowness is caused by the use of a small value of the regularization parameter, continuation schemes have been found quite effective in speeding up the algorithm. The key observation is that IST algorithm benefits significantly from warm-starting, i.e., from being initialized near a minimumof the objective function. This suggests that we can use the solution of (1), for a given value of τ, to initialize IST in solving the same problem for a nearby value of τ. Thiswarm-starting property underlies continuation schemes. The idea is to use IST to solve (1) for a larger value of τ (which is usually fast), then decrease τ in steps toward itsdesired value, running IST with warm-start for each successivevalue of τ. |
IMAGE DECONVOLUTION WITH PERIODIC BC USING ADMM
|
The ADMM:
|
| The application of ADMM to our particular problem involves solving a linear system with the size of the unknown image or with the size of its representation. Although this seems like an unsurmountable obstacle, we show that it is not the case. In many problems, such as (circular) deconvolution, reproduction of missing samples, or reconstruction from partial Fourier observations, this system can be solved very quickly in closed form (with O(n) or O(n log n) cost). For problems of the form (1), we show how exploiting the fact that W is a tight Parseval frame, this system can still be solved efficiently (typically with O(n log n) cost. |
| We report results on a set of benchmark problems, including image deconvolution, recovery of missing pixels, and reconstruction from partial Fourier transform, using both frame-based regularization. In all the experiments, the resulting algorithm is consistently and considerably faster than the previous state of the art methods FISTA, TwIST, and SpaRSA. |
| Consider a generalization of an unconstrained optimization problem |
 |
Where 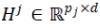 are arbitary matrices, and are arbitary matrices, and 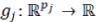 are convex functions.The instance of ADMM proposed in to so1lve(1) is presented in Algorithm 1, where are convex functions.The instance of ADMM proposed in to so1lve(1) is presented in Algorithm 1, where 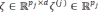 denotes the j-th block of ζ in the following partition denotes the j-th block of ζ in the following partition |
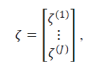 |
| and a similar notation is used for uk and dk. |
| Lines 4 and 6 of this algorithm are the main steps and those that can pose computational challenges. These steps, however, wereshown to have fast closed-form solutions in several cases of interest. In particular, the matrix inversion in line 4 cansometimes (e.g., in periodic deconvolution problems) be computedcheaply, by exploiting the matrix inversion lemma, the FFT and otherfast transforms (see [1, 13]), while line 6 corresponds to a so-calledMoreau proximity operator (MPO), defined as |
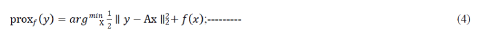 |
| for several choices of f, proxf has a simple closed form. |
 |
Under the condition that (1) has a solution, Algorithm 1 inherits the convergence guarantees of ADMM given in [11]. For our formulation, sufficient conditions for Algorithm 1 to converge to a solution of 1 are: 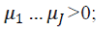 all functions gj are proper, closed, and convex; the matrix all functions gj are proper, closed, and convex; the matrix 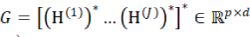 has full column rank (where()*denotes matrix/vector conjugate transpose,and has full column rank (where()*denotes matrix/vector conjugate transpose,and 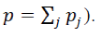 |
| Image deconvolution with periodic BC: This section reviews the ADMM-based approach to image deconvolution with periodic BC, using the frame-based formulations, the standard regularizers for this class of imaging inverse problems. We begin by considering the usual observation model used in image deconvolution with periodic BC: |
 |
where 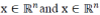 are vectors containing all pixels (lexicographically ordered) of the original and the observed images, respectively, w denotes white Gaussian noise, and are vectors containing all pixels (lexicographically ordered) of the original and the observed images, respectively, w denotes white Gaussian noise, and 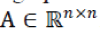 is the matrix representing the (periodic) convolution with some filter. In the frame-based analysis approach, the estimated image, is the matrix representing the (periodic) convolution with some filter. In the frame-based analysis approach, the estimated image, 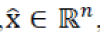 ,is obtained as ,is obtained as |
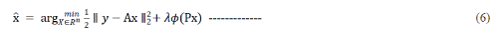 |
Where 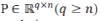 is the analysis operator of some frame (e.g., a redundant wavelet frame or a curvelet frame), Ø is a regularizer encouraging the vector of frame analysis coefficients to be sparse, and ?? > 0is the regularization parameter. A typical choice for Ø, herein adopted, is is the analysis operator of some frame (e.g., a redundant wavelet frame or a curvelet frame), Ø is a regularizer encouraging the vector of frame analysis coefficients to be sparse, and ?? > 0is the regularization parameter. A typical choice for Ø, herein adopted, is |
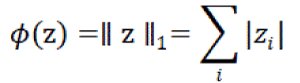 |
| Problem (6) can be written in the form (3), with J = 2 and |
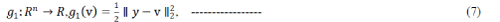 |
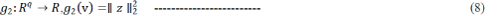 |
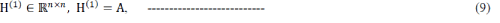 |
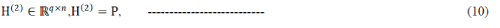 |
| The operators of g1 and g2, simple expressions of key components of Algorithm 1 (line 6), |
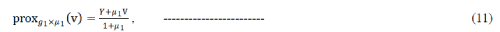 |
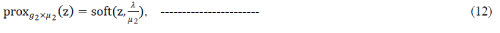 |
| where ?soft? denotes the well-known soft-threshold function |
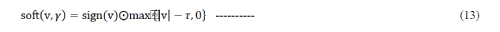 |
| where the sign, max, and absolute value functions are componentwise, and?denotes the component-wise product.Line 4 of Algorithm 1 (the other key component) has the form |
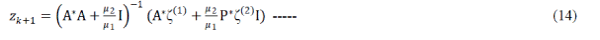 |
| Assuming that P corresponds to a Parseval1 frame (i.e., P*P = I,although possibly PP* ≠ I, the matrix inverse in (14) is simplycomputed in the DFT domain |
 |
| in which U and U*are the unitary matrices representing the DFT and its inverse, and Λ is the diagonal matrix of the DFT coefficients of the convolution kernel (i.e., A = U*ΛU). |
The inversion in (15) has O(n log n) cost, since matrix 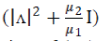 is diagonal and the products by U and U* can be computed using the FFT. The leading cost of each application of (14) (line 4 of Algorithm 1) is thus either the O(n log n) cost associated with (15) or the cost of the products byP*. For most tight frames used in image restoration, this product has fast O(n log n) algorithms. is diagonal and the products by U and U* can be computed using the FFT. The leading cost of each application of (14) (line 4 of Algorithm 1) is thus either the O(n log n) cost associated with (15) or the cost of the products byP*. For most tight frames used in image restoration, this product has fast O(n log n) algorithms. |
| We conclude that, under periodic BC and for a large class of frames, each iteration of Algorithm 1 for solving (5) has O(n log n) cost. Finally, this instance of ADMM has convergence guarantees, since: (1)g2 is coercive, so is the objective function in (5), thus its set of minimizers is not empty, (2)g1 and g2 are proper, closed,convex functions; (3) matrix H(2) = Iobviously has full column rank, which implies that G = [A*I*]also has full column rank. |
| In the experiments herein reported, we use the benchmark Lena image(of size 256 × 256), with different blurs (outof- focus and uniform), all of size 19 × 19(i.e., 2l + 1 × (2l + 1), with l = 9), at four different BSNRs (blurred signal to noise ratio): 40dB, 50dB, and 60dB. The reason why we concentrate on large blurs is that the effect of the boundary conditions is very evident in this case. |
On each degraded image, the algorithm proposed in Section3.2 was run, as well as the periodic version (Section 3.1), with and without pre-processing the observed image with the ?edgetapper? MATLAB function. The algorithms are stopped when 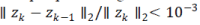 and λ was adjusted to yield the highest SNR of the reconstructed image. and λ was adjusted to yield the highest SNR of the reconstructed image. |
| Table 1 shows, for each blur and BSNR, the ISNR (improvement in SNR) values obtained with the two algorithms mentioned in the previous paragraph. The huge impact of wrongly assuming periodic BC is clear in these results, as well as in the example shown in Fig. 2. |
DECONVOLUTION WITH UNKNOWN BOUNDARIES
|
The observation model
|
| To handle images with unknown boundaries, we model the boundary pixels as unobserved, which is achieved my modifying(5) into |
 |
| whereM ∈ {0, 1}m×n (with m <w) is a masking matrix, i.e., A is replaced by MA, in line 8, while in line 6, A_ is replaced by A*M*and K is redefined (instead of (33)) as the inverse of the matrix in convolution represented by A is irrelevant, and we may adopt periodic BCs, for computational convenience. |
| If M = I, model (34) reduces to a standard periodic |
 |
| deconvolution problem. Conversely, if A = I, (34) becomes a pure inpainting problem. Moreover, the formulation (34) canbe used to model problems where not only the boundary, butalso other pixels, are missing, as in standard image Inpainting. |
Frame Based Deconvolution With Unknown Boundaries
|
| A. Frame-Based Analysis Formulation |
| Mask Decoupling (MD): The frame-based analysis formulation corresponding to observation model is |
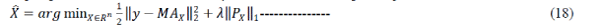 |
| B. Frame-Based Synthesis Formulation |
| Mask Decoupling (MD): Under observation model the frame-based synthesis formulation changes to |
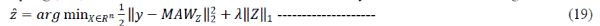 |
| C.Frame Synthesis Conjugate Gradient |
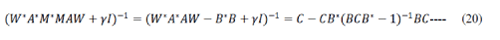 |
where the second equality results from using the Sherman-Morrison-Woodbury matrix inversion identity, after defining Since 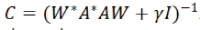 A is circulant, C can be efficiently computed via FFT, as A is circulant, C can be efficiently computed via FFT, as 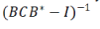 explained in the inversion. explained in the inversion. |
| 4.3 TV based deconvolution with unknown boundaries |
| A.Mask Decoupling (MD): Given the observation model, TV-based deconvolution with unknown boundaries is formulated as |
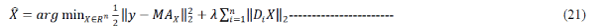 |
| B.TV conjugate gradient |
| The consequence is a simple modification of Algorithm , where |
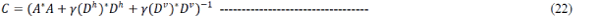 |
| The circulant nature of A, Dh, and Dv allows computing C efficiently in the DFT domain. |
SIMULATION RESULTS
|
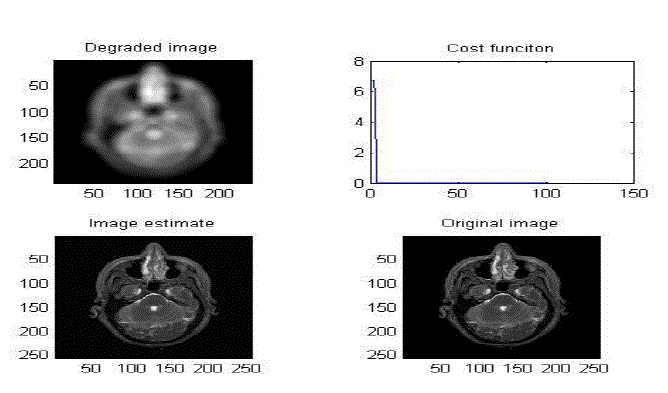
| The simulation studies involve the output of the proposed method based on the ADMM is shown in the fig3. It includes the original image and the degraded image after performing the ADMM algorithm it will produce the estimated image. The cost function will indicate the number of iterations to obtain the estimated image from the degraded image. The ISNR values of the estimated image is tabulated in the table.2 based on frame analysis and total variation algorithms which are used in ADMM. |
CONCLUSION
|
| Presented a new strategy to extend recent fast image deconvolution algorithms, based on the alternating direction method of multipliers (ADMM), to problems with unknown boundary conditions. Considered frame based analysis formulation,and gave the convergence guarantees for the algorithms proposed. Experiments show the results in terms of restoration quality.Ongoing and future work includes theinstead of adopting a standard BC or a boundary smoothing scheme, a more realistic model of actual imaging systems treats the external boundary pixels as unknown; i.e., the problem is seen as one of simultaneous deconvolution and inpainting, where the unobserved boundary pixels are estimated together with the deconvolved image. |
| |
Tables at a glance
|
 |
 |
| Table 1 |
Table 2 |
|
| |
Figures at a glance
|
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
|
| |
References
|
- M. Afonso, J. Bioucas-Dias, and M. Figueiredo, “Fast image recovery using variable splitting and constrained optimization,” IEEE Trans. Image Proc., vol. 19, pp. 2345–2356, 2010.
- An augmented Lagrangian approach to the constrainedoptimization formulation of imaging inverse problems,” IEEETrans. Image Proc., vol. 20, pp. 681–695, 2011.
- A. Beck and M. Teboulle, “A fast iterative shrinkagethresholding algorithm for linear inverse problems,” SIAMJour. Imaging Sciences, vol. 2, pp. 183–202, 2009.
- J. Bioucas-Dias and M. Figueiredo, “A new TwIST: two-stepiterative shrinkage/thresholding algorithms for image restoration,” IEEE Trans. Image Proc., vol. 16, pp. 2992–3004, 2007.
- S. Boyd, N. Parikh, E. Chu, B. Peleato, and J. Eckstein, “Distributed optimization and statistical learning via the alternatingdirection method of multipliers,” Foundations and Trends inMachine Learning, vol. 3, pp. 1–122, 2011.
- T. Chan, A. Yip, and F. Park, “Simultaneous total variation image inpainting and blind deconvolution,” International Journalof Imaging Systems and Technology, vol. 15, pp. 92–102, 2005.
- P. Combettes and J.-C. Pesquet, “Proximal Splitting Methodsin Signal Processing”, in Fixed-Point Algorithms for InverseProblems in Science and Engineering (H. Bauschke et al, Editors), pp. 185–212, Springer, 2011.
- P. Combettes and V. Wajs, “Signal recovery by proximalforward-backward splitting,” SIAM Journal on MultiscaleModeling & Simulation, vol. 4, pp. 1168–1200, 2005.
- I. Daubechies, M. Defrise, C. De Mol, “An iterative thresholding algorithm for linear inverse problems with a sparsity constraint,” Comm. Pure and App. Math., vol. 57, pp. 1413–1457,2004.
- M. Donatelli, C. Estatico, A. Martinelli, and S. SerraCapizzano, “Improved image deblurring with anti-reflectiveboundary conditions and reblurring,”Inverse Problems,vol. 22, pp. 2035–2053, 2006.
|