Performance of Decision Trees for Assessment
of the Risk Factors of Heart Disease

Dr.K.P.Kaliyamurthie; D.Parameswari

Performance of Decision Trees for Assessment of the Risk Factors of Heart Disease

Dr.K.P.Kaliyamurthie¹, D.Parameswari²

Professor and Head, Dept. of IT, Bharath University, Chennai, TN, India
Asst. Prof.(SG), Dept. of Computer Applications, Jerusalem College of Engg., Chennai, TN, India

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering

Abstract

Coronary heart disease refers to the failure of coronary circulation to supply adequate circulation to cardiac muscle and surrounding tissue. The events myocardial infarction (MI), percutaneous coronary intervention (PCI), and coronary artery bypass graft surgery (CABG) were investigated The risk factors investigated were: 1) before the event: a) no modifiable—age, sex, and family history for premature CHD, b) modifiable—smoking before the event, history of hypertension, and history of diabetes; and 2) after the event: modifiable—smoking after the event, systolic blood pressure, diastolic blood pressure, total cholesterol, high- density lipoprotein, low-density lipoprotein, triglycerides, and glucose.. Data-mining analysis was carried out using the C5 decision tree algorithm for the aforementioned three events using five different splitting criteria. C4.5 is a widely-used free data mining tool that is descended from an earlier system called ID3 and is followed in turn by C5.0. It embodies new algorithms for generating rule sets, and the improvement is dramatic in accuracy, speed and memory.

Keywords

Coronary Heart Disease (CHD), data mining, de- cession trees, risk factors

INTRODUCTION

Coronary Heart Disease (CHD) is usually caused by a condition called atherosclerosis, which occurs when fatty material and other substances form a plaque build-up on the walls of your arteries. This causes them to get narrow. As the coronary arteries narrow, blood flow to the heart can slow down or stop. This can cause chest pain (stable angina), shortness of breath, heart attack, and other symptoms, usually when you are active. CHD is the leading cause of death in the world for men and women. Many things increase your risk for heart disease: Men in their 40s have a higher risk of CHD than women. But as women get older (especially after they reach menopause), their risk increases to almost equal that of a man's risk.. Bad genes (heredity) can increase your risk. You are more likely to develop the condition if someone in your family has a history of heart disease -- especially if they had it before age 50. Your risk for CHD goes up the older you get. Diabetes is a strong risk factor for heart disease. High blood pressure increases your risks of coronary artery disease and heart failure. Abnormal cholesterol levels: your LDL ("bad") cholesterol should be as low as possible, and your HDL ("good") cholesterol should be as high as possible to reduce your risk of CHD.

Metabolic syndrome refers to high triglyceride levels, high blood pressure, excess body fat around the waist, and increased insulin levels. People with this group of problems have an increased chance of getting heart disease. Smokers have a much higher risk of heart disease than non-smokers. Chronic kidney disease can increase your risk. Already having atherosclerosis or hardening of the arteries in another part of your body (examples are stroke and abdominal aortic aneurysm) increases your risk of having coronary heart disease. Other risk factors include alcohol abuse, not getting enough exercise, and having excessive amounts of stress. Higher-than-normal levels of inflammation-related substances, such as C-reactive protein and fibrinogen are being studied as possible indicators of an increased risk for heart disease. Increased levels of a chemical called homocysteine, an amino acid, are also linked to an increased risk of a heart attack.

DECISION TREE LEARNING

A. Data Collection, Cleaning, and Coding

Decision tree learning, used in statistics, data mining and machine learning, uses a decision tree as a predictive model which maps observations about an item to conclusions about the item's target value. More descriptive names for such tree models are classification trees or regression trees. In these tree structures, leaves represent classifications and branches represent conjunctions of features that lead to those classifications.In decision analysis, a decision tree can be used to visually and explicitly represent decisions and decision making. In data mining, a decision tree describes data but not decisions; rather the resulting classification tree can be an input for decision making. This page deals with decision trees in data mining.coronary intervention (PCI), or coronary artery bypass graft surgery (CABG).

Data for each subject were collected as given in Table I: 1) risk factors before the event, a) nonmodifiable— age, sex, and family history (FH); 2) modifiable—smoking before the event (SMBEF), history of hypertension (HxHTN), and history of diabetes (HxDM); and 2) risk factors after the event, modifiable—smoking after the event (SMAFT), systolic blood pressure (SBP) in mmHg, diastolic blood pressure (DBP) in mmHg, total cholesterol (TC) in mg/dL, high-density lipoprotein (HDL) in mg/dL, low-density lipoprotein (LDL) in mg/dL, triglycerides (TG) in mg/dL, and glucose (GLU) in mg/dL. To clean the data, the fields were identified, duplications were extracted, missing values were filled, and the data were coded as given in Table 1.

I. After data cleaning, the number of cases was reduced as given in Table II, mainly due to unavailability of biochemical results.

B. Classification by Decision Trees

The C5.0 algorithm [25], which uses the divide-and-conquer approach to decision tree induction, was employed. The algorithm uses a selected criterion to build the tree. It works top–down, seeking at each stage an attribute to split on that which best separates the classes, and then recursively processing the sub problems that result from the split. The algorithm uses heuristics for pruning derived based on the statistical significance of splits.

Algorithm Generate Decision Tree [25], [26]:

Input:

1) Training dataset D, which is a set of training observations and their associated class value.

2) Attribute list A, the set of candidate attributes.

3) Selected splitting criteria method.

Output: A decision tree.

Method:

1) Create a node Nd

2) If all observations in the training dataset have the sameclass output value C, then return Nd as a leaf node labeled with C.

3) If attribute list is empty, then return Nd as leaf node labeled with majority class output value in training dataset.

4) Apply selected splitting criteria method to training dataset in order to find the ‘‘best” splitting criterion attribute.

5) Label node Nd with the splitting criterion attribute.

6) Remove the splitting criterion attribute from the attribute list.

7) For each value j in the splitting criterion attribute.

a) Let Dj be the observations in training dataset satisfying attribute value j.

b) If Dj is empty (no observations), then attach a leaf node labeled with the majority class output value to node Nd.

c) Else attach the node returned by generate decision tree (Dj , attribute list, selected splitting criteria method) to node Nd.

8) End for.

9) Return node Nd.

In this study, the following splitting criteria were investigated that are briefly presented shortly: information gain, gini index, likelihood ratio chi-squared statistics, gain ratio, and distance measure.

1) Information Gain (IG): Information gain is based on Claude Shannon’s work on information theory. InfoGain of an attribute A is used to select the best splitting criterion attribute. The highest InfoGain is selected to build the decision tree [27]

InfoGain(A) = Info(D) − InfoA (D) (2.1) where A is the attribute investigated.

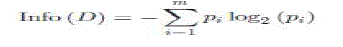where

pi = probability(class i in dataset D);

m = number of class values.

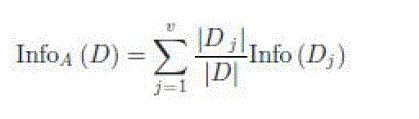where

|Dj | = number of observations with attribute value j in

dataset D;

|D| = total number of observations in dataset D;

Dj = sub dataset of D that contains attribute value j;

v = all attribute values.

Although information gain is usually a good measure for deciding the relevance of an attribute, it is not perfect. A problem occurs when information gain is applied to attributes that can take on a large number of distinct values. When that happens, then gain ratio is used instead.

2) Gini Index (GI): The Gini index is an impurity-based criterion that measures the divergence between the probability distributions of the target attributes values [28]

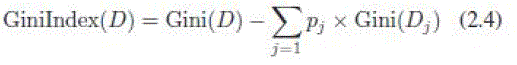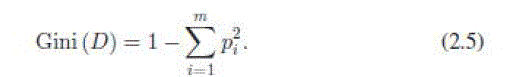3) Likelihood Ratio Chi-Squared Statistics (χ2 ): The likelihood ratio chi-squared statistic is useful for measuring the statistical significance of the information gain criterion [29]

G2 (A,D) = 2 × ln (2) × |D| × InfoGain (A) . (2.6)

4) Gain Ratio (GR): Gain ratio biases the decision tree against considering attributes with a large number of distinct values. So it solves the drawback of information gain [25]

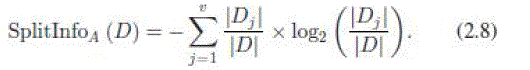5) Distance Measure (DM): Distance measure, like GR, normalizes the impurity criterion (GI). It suggests normalizing it in a different way [30]

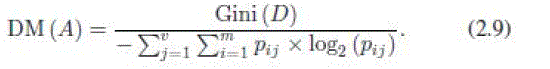A data-mining tool was developed by our group that supports the C5.0 decision tree algorithm using the aforementioned criteria. Overfitting is a significant practical difficulty for decision tree learning. Therefore, pruning is implemented to avoid overfitting. We implemented the bottom-up pruning algorithm using Laplace error estimation. While the decision tree is built and a leaf node is created, then the Laplace error [31] is estimated as follows:

E (D) = N − n + m – 1/N + m (2.10)

where

C = class value majority class in D;

N = number of observations in D;

n = number of observations has class value C.

As the algorithm returns to the root node, the error of the leaf node is passed to the father node. The father node calculates the total error of all of its children and its own error. If the father’s error is less than the total error of the children, then the father node is pruned and replaced by a leaf node with the majority class value. If the father’s error is greater than the total error of the children, then no more pruning is done to the path and the returned error is zero.

C. Classification Models Investigated

The following sets of models were investigated as given in

Table II.

1) MI:MI versus non-MI. Subjects having myocardial infarction were marked as symptomatic and the rest as asymptomatic.

2) PCI: PCI versus non-PCI. Subjects having only PCI were marked as symptomatic and the rest as asymptomatic. Subjects having both PCI and MI were excluded.

3) CABG: CABG versus non-CABG. Subjects having only

CABG were marked as symptomatic and the rest as asymptomatic. Subjects having both CABG and MI were excluded. For each set of models, three different subsets of runs were carried out as given in the following:

1) with risk factors before the event (B);

2) with risk factors after the event (A); and

3) with risk factors before and after the event (B + A). For each model, for each splitting criterion, 20 runs were carried out with random sampling [32] of equal number of cases used for training and evaluation as given in Table II. A total of 300 runs were carried out for each set of models [i.e., 20 runs × 5 splitting criteria × 3 (for B, A, and B +A datasets)]. The Wilcoxon rank sum test [33] was also carried out to investigate if there was or not significant difference between the five splitting criteria used as well as between the B, A, and B + A decision tree models at p < 0.05.

D. Performance Measures

In order to evaluate the performance of our results we used the following measures.

1) Correct classifications (%CC): is the percentage of the correctly classified records; equals to (TP + TN)/N.

2) True positive rate (%TP): corresponds to the number of positive examples correctly predicted by the classification model.

3) False positive rate (%FP): corresponds to the number of negative examples wrongly predicted as positive by the classification model.

4) True negative rate (%TN): corresponds to the number of negative examples correctly predicted by the classification model.

5) False negative rate (%FN): corresponds to the number of positive examples wrongly predicted as negative by the classification model.

6) Sensitivity: is defined as the fraction of positive examples predicted correctly by the model, equals to TP/(TP +FN).

7) Specificity: is defined as the fraction of negative examples predicted correctly by the model, equals to TN/(TN+FP).

8) Support: is the number of cases for which the rule applies (or predicts correctly; i.e., if we have the rule X → Z, Support is the probability that a transaction contains {X, Z} [26]

9) Confidence: is the number of cases for which the rule applies (or predicts correctly), expressed as a percentage of all instances to which it applies (i.e., if we have the rule X → Confidence is the conditional probability that a transaction having X also contains Z) [26]

Confidence = P (Z|X) = P (XZ) P (X) .

E. Calculation of the Risk

For each subject, we used the Framingham equation [8]–[10] to calculate the risk for an event to occur. We separated the subjects into two categories, those who have had an event and those who have not had an event. Then, for each extracted rule, we found out the subjects matching that rule and computed the average event risk per rule based on the risk value of each subject (see last two columns of Table V). It is noted that values of risk lower than 5%, between 5–10%, and higher than 10% classify a subject as low, intermediate, and high risk, respectively.

Conclusion

1) a data mining system was proposed to extract rules for CHD events, 2) the rules extracted facilitated the grouping of risk factors into high and low risk factors, and 3) the rules extracted are associated with an event risk, however, this needs further investigation.

Tables at a glance


Table 1	Table 2

References

“Assessment of the Risk Factors of Coronary Heart Events Based on Data Mining With Decision Trees” , Minas A. Karaolis, Member, IEEE, Joseph A. Moutiris, DemetraHadjipanayi, and Constantinos S. Pattichis, Senior Member, IEEE

Euroaspire study group, “A European Society of Cardiology survey of secondary prevention of coronary heart disease: Principal results,” Eur. Heart J., vol. 18, pp. 1569–1582, 1997.

Euroaspire II Study Group, “Lifestyle and risk factor management and use of drug therapies in coronary patients from 15 countries,” Eur. Heart J., vol. 22, pp. 554–572, 2002.

Euroaspirestusy group, “Euroaspire III: A survey on the lifestyle, risk factors and use of cardioprotective drug therapies in coronary patients from 22 European countries,” Eur. J. Cardiovasc. Prev. Rehabil., vol. 16, no. 2, pp. 121–137, 2009.

W. B. Kannel, “Contributions of the Framingham Study to the conquest of coronary artery disease,” Amer. J. Cardiol., vol. 62, pp. 1109–1112, 1988.

M. Karaolis, J. A.Moutiris, and C. S. Pattichis, “Assessment of the risk of coronary heart event based on data mining,” in Proc. 8th IEEE Int. Conf. Bioinformatics Bioeng., 2008, pp. 1–5.

Z. Wang and W. E. Hoy, “Is the Framingham coronary heart disease absolute risk function applicable to Aboriginal people?” Med. J. Australia, vol. 182, no. 2, pp. 66–69, 2005.

P. Brindle, J. Emberson, F. Lampe, M.Walker, P.Whincup, T. Fahey, and S. Ebrahim, “Predictive accuracy of the Framingham coronary risk score in British men: Prospective cohort study,” Br. Med. Assoc., vol. 327, pp. 1267–1270, 2003.

S. Sheridan, M. Pignone, and C. Mulrow, “Framingham-based tools to calculate the global risk of coronary heart disease: A systematic review of tools for clinicians,” J. Gen. Intern. Med., vol. 18, no. 12, pp. 1060–1061, 2003.

T. A. Pearson, S. N. Blair, S. R. Daniels, R. H. Eckel, J. M. Fair, S. P. Fortmann, B. A. Franklin, L. B. Goldstein, Ph. Greenland, S. M. Grundy, Y. Hong, N. H. Miller, R.M. Lauer, I. S. Ockene, R. L. Sacco, J. F. Sallis, S. C. Smith, N. J. Stone, and K. A. Taubert, “AHA guidelines for primary prevention of cardiovascular disease and stroke,” Circulation, vol. 106, no. 3, pp. 388–391, 2002.

S. M. Grundy, R. Pasternak, P. Greenland, S. Smith, and V. Fuster, “Assessment of cardiovascular risk by use of multiple-risk-factor assessment equations,” Amer. Heart Assoc., vol. 100, pp. 1481–1492, 1999.

V. Podgorelec, P. Kokol, B. Stiglic, and I. Rozman, “Decision trees: An overview and their use in medicine,” J. Med. Syst., vol. 26, no. 5, pp. 445– 463, 2002.

C. Ordonez, “Comparing association rules and decision trees for disease prediction,” in Proc. Int. Conf. Inf. Knowl.Manage.,Workshopealthcare Inf. Knowl. Manage. Arlington, VA, 2006, pp. 17–24.

C. Ordonez, E. Omiecinski, L. de Braal, C. A. Santana, N. Ezquerra, J. A. Taboada, D. Cooke, E. Krawczvnska, and E. V. Garcia, “Mining constrained association rules to predict heart disease,” in Proc. IEEE Int. Conf. Data Mining (ICDM 2001), pp. 431–440.

D. Gamberger and R. Bo?skovi´c Institute, Zarageb, Croatia, “Medical prevention: Targeting high-risk groups for coronary heart disease,” Sol-EU-Net: Data Mining Decision Support [Online]. Available: http://soleunet.ijs.si/website/other/case_solutions/CHD.pdf.

C. L. Tsien, H. S. F. Fraser, W. J. Long, and R. L. Kennedy, “Using classification trees and logistic regression methods to diagnosemyocardialinfraction,” in Proc. 9th World Congr. Med. Inf., vol. 52, pp. 493–497, 1998.

R. B. Rao, S. Krishan, and R. S. Niculescu, “Data mining for improved cardiac care,” ACM SIGKDD Explorations Newslett., vol. 8, no. 1, pp.3– 10, 2006.

J. Zavrsnik, P. Kokol, I. Maleiae, K. Kancler, M. Mernik, and M. Bigec, “ROSE: Decision trees, automatic learning and their applications in cardiac medicine,” Medinfo, vol. 8, no. 2, p. 1688, 1995.

K. Polat, S. Sahan, H. Kodaz, and S. Guenes, “A hybrid approach to medical decision support systems: combining feature selection, fuzzy weighted pre-processing and AIRS,” Comput.Methods Programs Biomed., vol. 88, no. 2, pp. 164–174, 2007.

S. A. Pavlopoulos, A. Ch. Stasis, and E. N. Loukis, “A decision treebased method for the differential diagnosis of aortic stenosis from mitral regurgitation using heart sounds,” Biomed. Eng. OnLine, vol. 3, p. 21, 2004.

C. A. Pena-Reyes, “Evolutionary fuzzy modeling human diagnostic decisions,” Ann. NY Acad. Sci., vol. 1020, pp. 190–211, 2004.

K. Boegl, K.-P.Adlassnig, Y. Hayashi, T. E. Rothenfluh, and H. Leitich, “Knowledge acquisition in the fuzzy knowledge representation framework of amedical consultation system,” Artif.Intell.Med., vol. 30, no. 1, pp. 1– 26, 2004.

D. Michie, D. J. Spiegelhalter, and C. C. Taylor, Machine Learning, Neural and Statistical Classification. West Susser, England: Ellis Horwood, 1994.

J. R. Quinlan, in C4.5 Programs for Machine Learning, C. Schaffer, Ed. San Mateo, CA: Morgan Kaufmann, 1993.

J. Han and M. Kamber, Data Mining, Concepts and Techniques, 2nd ed. San Francisco, CA: Morgan Kaufmann, 2001.

J. R. Quinlan, “Simplifying decision trees,” Int. J. Man-Mach. Stud., vol. 27, pp. 221–234, 1987.

L. Breiman, J. Friedman, C. J. Stone, and R. A. Olshen, Classification and Regression Trees. Belmont, CA: Wadsworth Int. Group, 1984.

F. Attneave, Applications of Information Theory to Psychology. New York: Holt, Rinehart, and Winston, 1959.

R. Lopez de Mantras, “A distance-based attribute selection measure for decision tree induction,” Mach. Learn., vol. 6, pp. 81–92, 1991.

T. Niblett, “Constructing Decision trees in noisy domains,” in Proc. 2nd Eur. Working Session Learn., 1987, pp. 67–78.

L. Rokach and O.Maimon, Data Mining with Decision Trees, Theory and Applications. Singapore: World Scientific, 2008.

F. Wilcoxon, “Individual comparisons by ranking methods,” Biometrics, vol. 1, pp. 80–83, 1945.