International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Menu

ISSN ONLINE(2320-9801) PRINT (2320-9798)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Processing Uncertain Databases Using USkyline Mechanism

Navya.E.K1, M.Madhan Kumar2
  1. PG Scholar, Department of CSE, Hindusthan Institute of Technology, Coimbatore, India
  2. Asst. Professor, Department of CSE, Hindusthan Institute of Technology, Coimbatore,India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Abstract

Skyline computation is been widely used in multicriteria data analysis and decision making. As research in uncertain databases draws increasing attention, skyline queries with uncertain data have also been studied.For databases that having uncertain values,a probabilistic skyline query called p-skyline,has been developed to return skyline tuples.This has been achieved by using a probability threshold..The answer obtained by the P-skyline query usually includes the skyline tuples undesirably dominating each other when a small threshold is specified.To address this concern ,we propose a new uncertain skyline query called U-Skyline query in this paper.The U-Skyline query searches for a set of tuples that has the highest probability as the skyline answer.In order to answer U-Skyline queries efficiently,a number of optimization techniques for query processing is been used in this paper.

Keywords
Skyline query,uncertain databases ,LCM v.2 algorithm.

INTRODUCTION
Today, a number of indirect data collection methodologies have led to the proliferation of uncertain data. Such type of databases are much more complex because they having the additional challenges of representing the probabilistic information. Skyline queries with uncertain databases is of great importance in the field of data mining. Skyline queries are widely used in multicriteria decision making, where a choice that scores high in one criterion may score low in another. The query returns all data points that are not dominated by any other point in a dataset, where a point p1 dominates another point p2 if p1 is no worse than p2 in all dimensions and better than p2 in atleast one dimension. The points returned by a skyline query are called skyline points in the database community. The skyline tuples are considered to be important because they exhibit the properties of Non dominance, Incomparability and Coverage.
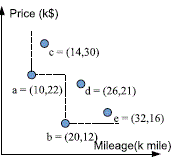
The skyline query has received its significant attention from the database community .Many variants of the skyline query and challenging research issues have been studied in the previous papers. The following example illustrates the skyline query. Suppose a user Ram wants to buy a used car and graphs the vehicle data set in Fig. 1a in terms of price and mileage. From the figure, we can see that vehicle a and b are the best choices because other vehicles are all inferior to either a or b in atleast one attribute and not better than them in all the other attributes (e.g., d has a higher price and a higher mileage than b and, thus, is inferior to b). Therefore, the answer for the skyline query upon this data set is {a,b} which forms a skyline that dominates the rest of vehicles.
The skyline query processing has great significance in real time applications. It may include the selling of a used car by online bidding services.For the selling of a used car,it having two constraints that are mileage and its price.
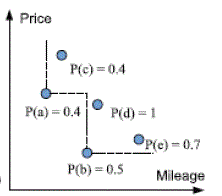
Generally,uncertainity of data arises inherently from various causes,such as incomplete survey results, data measure and collection methods,statistical and data mining techniques, and so on.Because of that in many real life applications, databases contain incomplete, noisy,outdated and uncertain data. In this paper, we propose a new uncertain skyline operator, namely, U-Skyline, that aims to return an uncertain skyline answer set from a different but complementary perspective to P-Skyline. Instead of considering individual tuples, U-Skyline focuses on returning an answer set that forms a valid skyline with the maximum probability. The probability associated with a skyline answer set to be valid among all the possible worlds is, thus, termed as U-Skyline probability. Here, we further compare U-Skyline and PSkyline in terms of the properties of nondominance, incompatibility, and coverage. Strictly speaking, both P-Skyline and U-Skyline do not possess the nondominance property exhibited in conventional database since they aim to return skyline tuples with threshold-qualified and highest probabilities, respectively. In other words, there is a chance for some non returned skyline tuples to dominate the returned tuples within some possible worlds. This is inherented from the nature of probabilistic queries for uncertain databases. Therefore, here we reconsider the nondominance property for uncertain database as “it’s not likely for returned skyline tuples to be dominated by nonanswer tuples.” Both PSkyline and U-Skyline have exhibited this property by ensuring the probability for the undesired scenario to be insignificant. For P-Skyline, by returning those tuples that are dominated by none or a few low probability tuples as the answer set, the probability that a P-Skyline answer set gets dominated by other nonanswer tuples is small. For USkyline, on the other hand, if a candidate skyline is dominated by other tuples, its U-Skyline probability is small and, thus, not likely to be the answer. Processing U-Skyline in a efficient manner is very critical. In addition to this, sophisticated analysis of the probability formula and development of pruning techniques of the search space are mandates. To meet these challenging needs, we made the following contributions in this paper:
1.We propose a new skyline query called U-skyline for uncertain data.It focuses of meeting the nondominance, incomparability and coverage , which are all the properties of a skyline query.
2.The LCM version 2 algorithm is been used here which having some additional techniques than version 1.The techniques are database reduction for fast checking, closedness and new pruning algorithm for backtracking based maximal frequent itemset mining.

LITERATURE SURVEY
Previous papers are studied in this work to identify the techniques that are used for processing uncertain databases and we notify the drawbacks occurred in the existing system.some of the related papers are been discussed here.

SLIDING WINDOW TOPK QUERIES ON UNCERTAIN STREAMS
Query processing on uncertain data streams has attracted a lot of attentions lately, due to the imprecise nature in the data generated from a variety of streaming applications, such as readings from a sensor network. However, all of the existing works on uncertain data streams study unbounded streams. This paper takes the first step towards the important and challenging problem of answering sliding-window queries on uncertain data streams, with a focus on arguably one of the most important types of queries—top-k queries. The challenge of answering sliding-window top-k queries on uncertain data streams stems from the strict space and time requirements of processing both arriving and expiring tuples in high-speed streams, combined with the difficulty of coping with the exponential blowup in the number of possible worlds induced by the uncertain data model. In this paper, we design a unified framework for processing sliding-window top-k queries on uncertain streams. We show that all the existing top-k definitions in the literature can be plugged into our framework, resulting in several succinct synopses that use space much smaller than the window size, while are also highly efficient in terms of processing time. In addition to the theoretical space and time bounds that we prove for these synopses, we also present a thorough experimental report to verify their practical efficiency on both synthetic and real data.

APPROACHING THE SKYLINE IN Z ORDER
Given a set of multidimensional data points, skyline query retrieves a set of data points that are not dominated by any other points. This query is useful for multi-preference analysis and decision making. By analyzing the skyline query, we observe a close connection between Z-order curve and skyline processing strategies and propose to use a new index structure called ZBtree, to index and store data points based on Z-order curve. We develop a suite of novel and efficient skyline algorithms, which scale very well to data dimensionality and cardinality, including (1) ZSearch, which processes skyline queries and supports progressive result delivery; (2) ZUpdate, which facilitates incremental skyline result maintenance; and (3) k-ZSearch, which answers k-dominant skyline query (a skyline variant that retrieves a representative subset of skyline results). Extensive experiments have been conducted to evaluate our proposed algorithms and compare them against the best available algorithms designed for skyline search, skyline result update, and k-dominant skyline search, respectively.

COMPUTING ALL SKYLINE PROBABILITIES FOR UNCERTAIN DATA
Skyline computation is widely used in multi-criteria decision making. As research in uncertain databases draws increasing attention, skyline queries with uncertain data have also been studied, e.g. probabilistic skylines. The previous work requires “thresholding” for its efficiency – the efficiency relies on the assumption that points with skyline probabilities below a certain threshold can be ignored. But there are situations where “thresholding” is not desirable – low probability events cannot be ignored when their consequences are significant. In such cases it is necessary to compute skyline probabilities of all data items. We provide the first algorithm for this problem whose worst-case time complexity is sub-quadratic. The techniques we use are interesting in their own right, as they rely on a space partitioning technique combined with using the existing dominance counting algorithm. The effectiveness of our algorithm is experimentally verified.

A SURVEY OF UNCERTAIN DATA ALGORITHMS AND APPLICATIONS
In recent years, a number of indirect data collection methodologies have led to the proliferation of uncertain data. Such databases are much more complex because of the additional challenges of representing the probabilistic information. In this paper, we provide a survey of uncertain data mining and management applications. We will explore the various models utilized for uncertain data representation. In the field of uncertain data management, we will examine traditional database management methods such as join processing, query processing, selectivity estimation, OLAP queries, and indexing. In the field of uncertain data mining, we will examine traditional mining problems such as frequent pattern mining, outlier detection, classification, and clustering. We discuss different methodologies to process and mine uncertain data in a variety of forms.

PROPOSED SYSTEM
The proposed system is a efficient method for skyline computation.In this paper,we propose a new skyline query for uncertain data. It focuses on meeting the nondominance, incomparability and coverage properties simultaneously for uncertain skyline query.A search algorithm based on dynamic programming (DP) to find U-Skyline is been used here. The algorithm is improved with pruning and early termination (P&ET) techniques. We propose input data set reduction (SR) and partition (SP) techniques to reduce the input data set size in order to further expedite the U-Skyline processing time.
For uncertain data processing ,an index tree is been constructed to store data at different levels.Here each data is providing an index. The index tree is been divided into different levels that are:

TOP LAYER
This layer includes nodes that are very frequently accessed during the mining process. These nodes are located in the upper levels of the I-Tree. They correspond to items with high support, which are distributed over few nodes with high node support. These items can be characterized by considering the average support of their nodes. As a first attempt, items whose average node support is larger than or equal to a given threshold Kavg may be assigned to the Top layer.

BOTTOM LAYER
This layer includes the nodes corresponding to rather low support items, which are rarely accessed during the mining process. Nodes in this layer are analyzed only when mining frequent item sets for very low support thresholds. The Bottom layer is characterized by a huge number of paths which are (possibly long) chains of nodes with unitary support. These sub paths represent (a portion of) a single transaction and are thus read only few times. A large number of low support items is included in this layer.

MIDDLE LAYER
This layer includes nodes that are quite frequently accessed during the mining process. These nodes are typically located in the central part of the tree. They correspond to items with relatively high support, but not yet dispersed on a large number of nodes with very low node support. We include in the Middle layer nodes with (node) support larger than 1. Unitary support nodes are rather rarely accessed and should be excluded from the Middle layer.

EXPERIMENTAL RESULTS
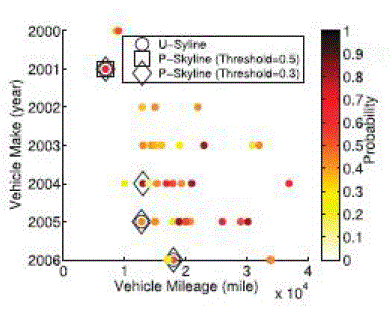
We conduct a comprehensive evaluation on the proposed U-Skyline query. Our experimental results demonstrate that the proposed algorithm is much faster than using a parallel integer programming solver to obtain U-Skyline.The Implementation of the LCM v.2 algorithm is loaded in memory for the support-based projection of the original database. The processing of U-skyline is an NP-hard problem. In U- skyline , there is no need to define the probability threshold and it also removes unwanted data from memory. So the memory space is been efficiently used. Here a dynamic programming framework for processing U-skyline is been used and developed a series of optimization techniques, including probability computational simplification, candidate skyline pruning and early termination, data set reducing to alleviate the computational strain. Moreover P-Skyline does not guarantee incomparability because tuples are selected individually after their nondominance probabilities are obtained. The below fig showing the comparison of Pskyline and U-skyline.
The above figure shows an example that uses a vehicle data to compare the P-skyline and U-skyline.Here mileage and the manufactured year are to be taken as the skyline criteria. As shown ,the lower left vehicles dominates the upper left vehicles. Also, the color points denotes the available probability. When the P-Skyline threshold is chosen as 0.5, only one upper left vehicle is selected, ending up with a biased result. Lowering the P-Skyline threshold to 0.3 addresses this coverage problem but the incomparability issue arises because the answer set contains one vehicle made in 2005 that dominates another vehicle made in 2004. Notice that the U-Skyline addresses both the coverage and incomparability issues well. In addition, trying various probability thresholds in P-Skyline may be tedious for users. On the contrary, USkyline does not require a threshold and always return the skyline result with the maximum probability.
Although U-Skyline has many good properties, U-Skyline is required to evaluate all data tuples as a whole instead of each individual tuple. Therefore, efficiently processing U-Skyline is very critical. For that ,we are used the LCM version 2 algorithm for enumerating frequent closed itemsets.

CONCLUSION
The field of the management of uncertain data has seen a revival in recent years. The reason for this is ,recently there are number of ways of collecting data which have resulted in the need for uncertain representations. These uncertain data can be handled using skyline computation. In this paper, we propose a new uncertain skyline operator called U-Skyline. We show that processing U-Skyline is an NP-hard problem. Thus,the processing of the Uskyline can be improved by using LCM v.2 algorithm. Here the techniques to be used are the database reduction for fast checking closedness and new pruning algorithm for backtracking based maximal frequent item set mining. We propose a dynamic programming framework for processing U-skyline and developed a series of optimization techniques, including probability computational simplification, candidate skyline pruning and early termination, data set reducing, and reduced set partition, to alleviate the computational strain. We compare our improved U-Skyline processing algorithms with the existing system and the results showed that our new algorithm is efficient than the existing system.
 

Figures at a glance
Figure 1a Figure 1b Figure 2
Figure 1a Figure 1b Figure 2
 

References