International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Menu

ISSN ONLINE(2319-8753)PRINT(2347-6710)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Reduction of Harmonic in a Multilevel Inverter Using Optimized Selective Harmonic Elimination Approach

Prof S.Parthasarathy1, R.Siva*2
 Department of Electrical and Electronics Engineering, K.L.N College of Engineering, Madurai, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Abstract

This paper adopts the Genetic Algorithm (GA) optimization technique for harmonic elimination in cascaded H-Bridge Multilevel inverter. The objective of the proposed work is to eliminate the lower order harmonics by deciphering non-linear equations corresponding to SHE. In this proposed work switching angles for power electronics switches present in the Multilevel Inverter are generated. The generated switching angle is optimized using GA for improving the accuracy of results. The results obtained shows the effectives of proposed work of it was verified using MATLAB software.

Keywords
Power quality, Total Harmonic Distortion, Multilevel inverter, Cascaded inverter, Selective Harmonic Elimination, Genetic Algorithm.

INTRODUCTION
Power Quality has been given consideration due to wide application of multilevel inverter for controlling and converting ac power and to feed electrical loads. These inverters are used at different power levels, ranging from large adjustable speed drives to low power household appliances. The huge amount of power pollution produced from this non-linear load has caused a voltage distortion. In recent year multilevel inverter are applied in industrial application such as power supplies, static VAR compensator, drive systems, etc. The multilevel inverter has several advantage compared to the two level Inverters such as lower common mode voltage, less dv/dt, lower harmonics in output voltage and reduced lower switching devices [1]-[4].
The Multilevel inverter is generally divided into three different categories: Diode Clamped Multilevel Inverter (DCMLI), Flying Capacitor Multilevel Inverter (FCMLI) and Cascaded Multilevel Inverter (CMLI) [3]. Among all topologies cascade multilevel inverters are capable of reaching medium voltage and high power applications levels using cascaded connection of several single phase inverters at low voltage level with better harmonic spectrum of output voltage. The CMLI topology is significant advantages, it requires least number of component compared to the DCMLI and FCMLI topology. The desired output of Multilevel Inverter contain on harmonic components as per IEEE 519-1992, IEC 61000-2-2 standards in the power systems [5]. To control the output voltage and to eliminate certain lower order harmonics in a multilevel inerter with equal dc sources, various control techniques are investigated such as Selective Harmonic Elimination (SHE), Sinusoidal Pulse Width Modulation (SPWM), Space Vector Modulation (SVM) [7]. However the PWM technique could not eliminate specific lower order harmonics such as 3rd to15th [6]. Multilevel inverter problem is used to find the switching angles. In this method switching angles are solved by non-linear transcendental equations which contain trigonometric terms. This set of transcendental equations can be solved by using iterative methods such as Newton-Raphsan (NR) method [8]. The N-R method initial values are must be initialized. Therefore N-R method will not able to solve the SHE problem for a large number of switching angles.
Genetic Algorithm (GA) has been proposed to solve the transcendental equations, [8]-[12]. Therefore in this proposed work by using an optimizing method like GA, an attempt is made to solve SHE equation whole range of modulation index and Total Harmonic Distortion (THD). In this proposed work single phase cascaded H-bridge five level inverter is chosen for analysis.

II. CMLI WITH SEPREATE DC SOURCE
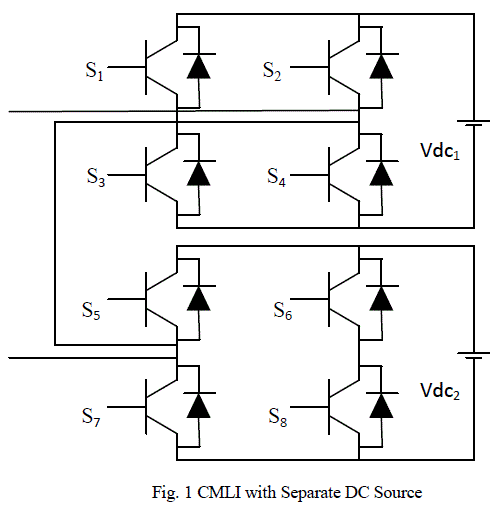
An Inverter structure, CMLI with separate DC source is familiarized here. This inverter avoids extra clamping diodes and a voltage balancing capacitor as a single phase structure. The AC terminal voltages of different voltage level inverters are connected in series. The basic structure of cascaded H-bridge inverter with separate dc source, show in Fig. 1.
The synthesized output voltage waveform of five level cascaded inverter is shown in Fig.2. The phase output voltage is synthesized by the summing the of inverter output, i.e. ) 1 2 ( a V a Van  V  . Each cell can generate three level of output +Vdc, 0, -Vdc. Each cell of inverter consist of four switches S1, S2, S3 and S4 using the first cell as example, turning on S1 and S4 yield V1 = +Vdc. Turning on S2 and S3 yield V1 = -Vdc. Turning off all switches yield V1 = 0. Correspondingly, the ac output voltage at each level can be obtained in the same manner. Minimum harmonic distortion can be attained by adjusting the switching angles of the inverter.
image

III. SELECTIVE HARMONIC ELIMINATION SWITCHING TECHNIQUE
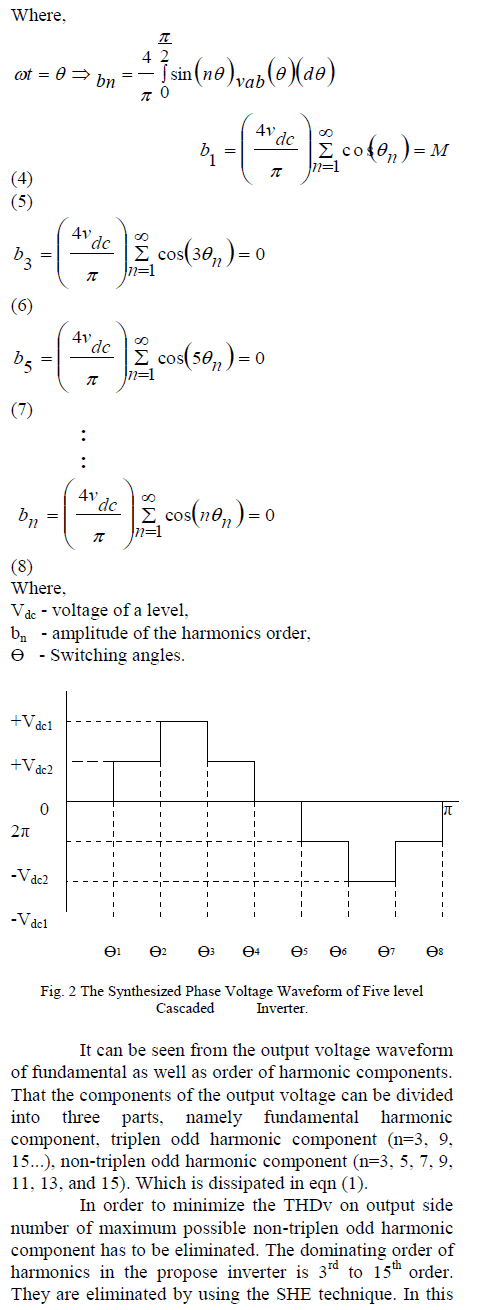image
image
proposed work switching angles for five level CMLI has been calculated by eliminating non-triplen odd harmonic components. The fundamental output voltage using SHE is given in eqn (5).

IV. OPTIMIZED SHE ALGORITHM
The working ability of GA is based on Darwin’s theory of ―survival of the fittest‖. GA contains chromosome, genes, set of population, fitness, fitness function, breeding, mutation and selection. GA begins with a set of solutions represented by chromosomes is called population. Solutions from one population are taken and used to form a new population, which is motivated by the possibility that the new population will be better than the old one. Additional, solutions are selected according to their fitness to form new solutions. The above process is repeated until termination condition is satisfied. GA is used for solving both constrained and unconstrained optimization problem based on natural selection. By the process of optimization the input of a CMLI is modified, mathematical process to obtain minimum or maximum of the output. The input of the optimization process is the objective function and the output is the switching angle of the CMLI.
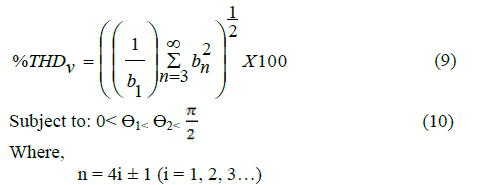image
In order to solve the SHE equation, GA is used to generating switching angles Ɵ1, Ɵ2 for a five level CMLI by varying modulation index from 0 to 1is subjected to elimination of lower of order harmonic components. Eqn (9) is selected as an objective function for the proposed optimization technique. The algorithm of proposed is follows,
1. Select floating point string.
2. Find the number of variables (number of switching angle is two).
3. Set a population size and initialize the population. When the population size is higher, increase the rate of convergence and also increase the execution time. The population is initialized between 0 degree and 180 degree taking into consideration of the full wave symmetry of output voltages.
4. Evaluate of fitness for each chromosome is the most important part of GA. The objective function is to minimize the specific lower order harmonics. In the proposed work, 3rd to 15th odd harmonics at the output side of a five level cascaded inverter are to be minimized.
5. Set the iteration count (100 iteration) to find the switching angles. Subsequently the first iteration, fitness values are used to determine a new offspring’s. These offspring under goes crossover and mutation. To create a new population.
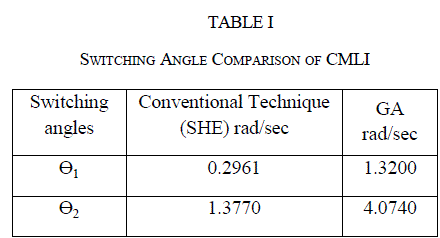
For each chromosome a five level output voltage are generated using the switching angles shown in Table 1 and harmonic magnitude are calculated using Fast Fourier Transformation analysis (FFT).

V. RESULT AND DISCUSSION
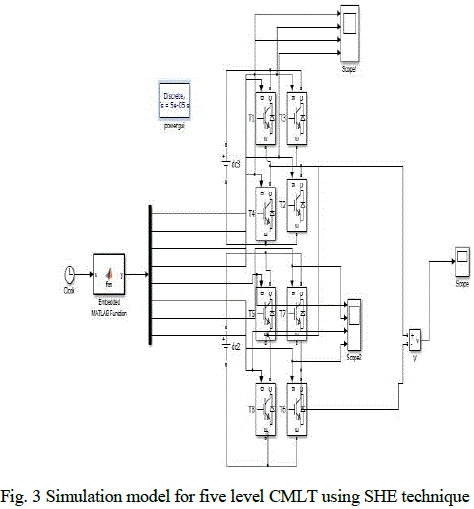
A single phase five level CMLI using SHE technique and variation of switching angles are simulated using MATLAB/Simulink. A five level inverter requires two bridges for simulation. IGBT’s are used as power switches. Fig. 3 shows the simulated circuit of five level CMLI using SHE technique.
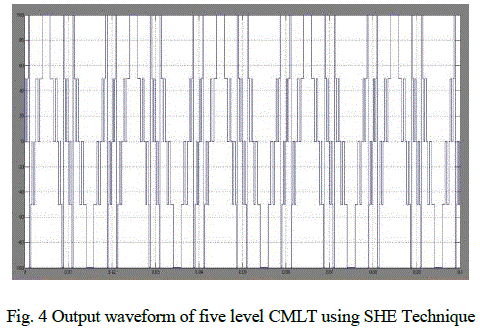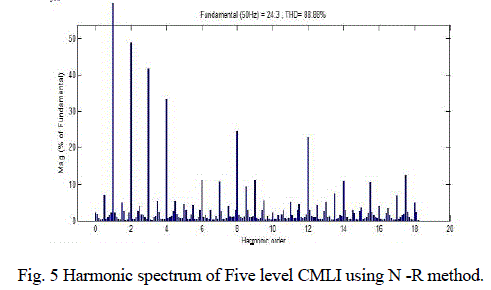
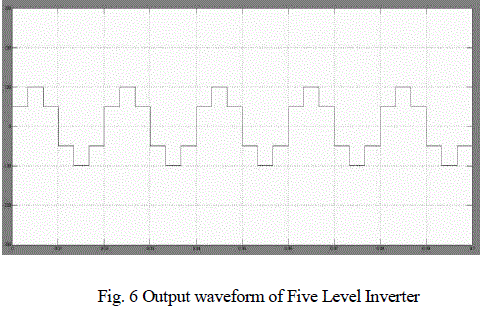
image
image
The proposed work is simulated using MATLAB/SIMULINK to check it validation. The parameters for simulation are as follows, voltage of each bridge (Vdc = 50v), frequency of the output voltage (f = 50Hz). The simulated waveform of the output voltage using SHE technique is shown in Fig. 4 from Fig. 5 the harmonic spectra of the output voltage can be viewed for further calculations. In GA’s, the calculated switching angles are simulated through the five level CMLI. The results are presented in this section. The output voltage waveform of the proposed work at M=0.55 is shown in Fig. 6. In order to clarify the amplitude of minimized harmonic spectra of the output voltage is shown in Fig. 7 in this case 3rd to 15th harmonic are minimized
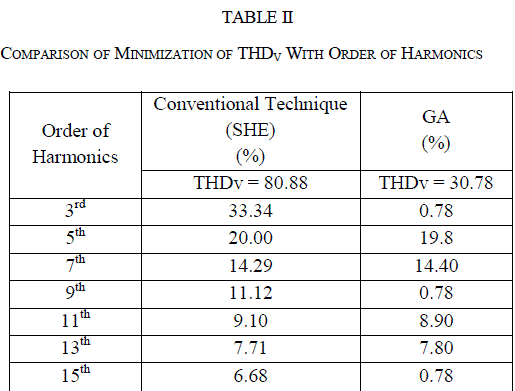
image
image
For each chromosome a five level output voltage is generated using the switching angles obtained from the proposed work as shown in Table 1 and required harmonic magnitude are calculated using FFT analysis. The Fig. 5 Depicts the harmonic profile of the output voltage is simulated with switching angles calculated from SHE technique by N-R method and Fig. 8 harmonic spectrum analysis it is inferred that the THDv when calculated using in GA was is 30.78% and that for N-R is 80.88%.
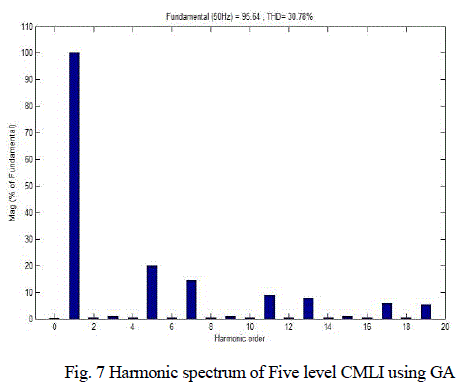image
From the Fig. 5 and Fig. 7 is obvious that the harmonics are reduced effectively by computing the switching angles by GA as compared to the N-R method. The proposed simulation studies have been conducted on Intel(R) core (TM) Duo 2, CPU T6400 @ 2.00 GHZ processor under MATLAB 2012b environment.
image
image

VI. CONCLUSION
In this paper GA optimization technique is applied to find the appropriated switching angles for the CMLI to eliminate harmonics. Selected order of harmonic are reduced and the fundamental output voltage is maintained at desired level, thus resulting in the minimum THDv. The proposed method reduces the harmonics component than any other conventional technique such as N-R method. The effectiveness of the proposed method has been verified through simulation and the results were presented. The results show that the proposed method effectively minimizes the dominating 3rd order harmonic.

References
  1. M.H.J. Bollen, ―What is power quality?‖, Electric Power Systems Research, Vol.66(2003),pp 5-14.
  2. Partha S. Bhowmik and S.Sengupta, ―Electric Power Quality in a Deregulated Power System: A Review‖, International Conference on Power Systems, ICPS (2004) , pp 83-88.
  3. J. Rodr´ guez, J. Lai, and F. Z. Peng, ―Multilevel inverters: A survey of topologies, controls and applications,‖ IEEE Trans. Ind. Electron., vol. 49, no. 4, pp. 724–738, Aug. 2002.
  4. J. S. Lai and F. Z. Peng, ―Multilevel converters—A new breed of power converters,‖ IEEE Trans. Ind. Appl., vol. 32, no. 3, pp. 509–517, May/Jun.1996.
  5. Duffey, C.K.; Stratford, R.P., "Update of harmonic standard IEEE-519-IEEE Recommended Practices and Requirements for Harmonic Control in Electric Power Systems," Industry Applications Society Annual Meeting, 1989., Conference Record of the 1989 IEEE , vol., no., pp.1618,1624 vol.2, 1-5 Oct. 1989.
  6. Wanmin Fei; Xiaoli Du; Bin Wu, "A Generalized Half-Wave Symmetry SHE-PWM Formulation for Multilevel Voltage Inverters," IEEE Trans. Ind. Appl., vol.57, no.9, pp.3030,3038, Sept. 2010.
  7. Krismadinata, Nasrudin ABD Rahim, Hew Wooi Ping, Jeyaral Selvaraj," Elimiantion of Harmonics in Photovoltaic Seven-level inverter with Newton-Raphson optimization", "procedia environment Sciences 17(2013) 519-528".
  8. Ozpineci, J. O. P. Pinto, and L. M. Tolbert, ―Pulse-width optimization in a pulse density modulated high frequency AC-AC converter using genetic algorithms,‖ in Proc. IEEE Int. Conf. Systems, Man, and Cybernetics,2001, pp. 1924–1929.
  9. I. Maswood, S.Wei, and M. A. Rahman, ―A flexible way to generate PWM-SHE switching patterns using genetic algorithms,‖ in Proc. IEEE Applied Power Electronics Conf. Expo., 2001, pp. 1130–1134.
  10. Houck, J.Joines, and M.Kay. The Genetic Algorithm Optimization Toolbox (GAOT) for MATLAB 5. [online]. Available:http://www.ie.ncsu.edu/mirage/GAToolBox/gaot.
  11. Pandi, P.M.; Devarajan, N., "Optimization of power quality in cascaded multilevel inverter-genetic algorithm approach," International Conference on Computing, Communication and Networking Technologies.,vol., no., pp.1,7, 29-31 July 2010.
  12. Ramkumar, S.; Kamaraj, V.; Thamizharasan, S., "GA based optimization and critical evaluation SHE methods for three-level inverter," International Conference on , Electrical Energy Systems (ICEES), 201 .,vol., no., pp.115,121, 3-5 Jan. 2011.