Research and Reviews - International Journals

International Journal of Innovative Research in Science, Engineering and Technology

Menu

ISSN ONLINE(2319-8753)PRINT(2347-6710)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Reliability of Dynamic Multi-State Oil Supply System by Structure Function

Fadhel S. F.1, Alauldin N. A.1 and Ahmed Y. Y.2
  1. Department of Mathematics and Computer Applications, College of Science, Al-Nahrain University, Baghdad, Iraq
  2. Information and Communication Technology Center, University of Technology, Baghdad, Iraq
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Abstract

Application of mathematical model of multi state system for oil supply system is considered in this paper. This paper describes a method for estimation of changes of one component states and its influence on themultistate system reliability by dynamic reliability indices. We examine the oil supply system to allow a different number of states for the oil supply system and for each pipelineby proposing dynamic reliability indices for investigation of this system. These indices estimate the influence upon the multi-state system reliability, which is the oil supply system from an oil source to three stations through several oil pipelines, say four. The mathematical approach of logical differential calculus is used for analysing the change in the multi-state system reliability that is caused by modification of some system components states.

Keywords
Multistate system reliability, Structure function, Dynamic reliability indices, Direct partial logic derivatives

INTRODUCTION
Hardware reliability has been increased by technological advances in large complex systems such as nuclear power plants, aircraft, and offshore oil plants, [16]. The basic concepts of MSS reliability were primarily introduced in the mid of the 1970's by Murchland in 1975, [11], [9], [3] and Ross in 1979, [14].Barlow and Wu in 1978 [1] characterize component state criticality as a measure of how a particular component state affects a specific system state.Griffithin 1980 [6] formalized the concept of MSS performance, and studied the impact of component improvement on the overall system reliability behaviour.The concepts of MSS important were also discussed in Block and Savits in1982 [2], where a decomposition theorem for MSS structure function was proved. Since that time, MSS reliability began with an intensive development. Essential achievements that were attained up to the mid of 1980's were reflected by Natvig in1985 [12], and by El-Neveihi and Prochan in 1984 [4], where it can be found the state of the art in the field of MSS reliability at this stage.
Readers that are more interested in the history and more ideas related to MSS reliability theory for the later work can find the corresponding overview in Lisnianski and Levitin [9] and Natvig [13].
There are some mathematical models in the reliability analysis. Firstly, it is the Binary System: the system and its components are allowed to have only two possible states (completed failure and perfect functioning). Secondly, it is the Multi-State System (MSS). In a MSS, both the system and its components may experience more than two states, for example, completely failed, partially functioning and perfect functioning. The reliability analysis of the binary system has served as a foundation for the mathematical treatment of the reliability theory. Many problem of the binary system have been settled. But this approach fails to describe many situations where the system can have more than two distinct states [9], [8]. Many practical components and systems have more than two different performance levels. For example, a power generator in a power station can work at full capacity, which is its nominal capacity, say 10MW, when there is no failure at all, [9]. Certain types of failures can cause the generator to be completely failed, while other failures will lead to the generator working at a reduced capacity say at 4 MW.
On the system level, let us consider a power generating system consisting of several power generators. The abilities of the system to meet high power load demand, normal power load demand and lower power load demand can be regarded as different system states.
Another example of multi-state components is an oil transmission pipeline [10]. The pipeline is used to transmit oil from the source to spots A, B and C aligned in order along the pipeline. We say that the pipeline is in state 0 when it cannot transmit oil to any of the spots; it is in state 1 if the oil can reach spot A; it is in state 2 if the oil can reach up to spot B, i.e., spot A and B; it is in state 3 if the oil can reach up to spot C. In the paper [19] authors had substantiated basic conceptions to apply the direct partial logic derivatives (it is part of logical differential calculus) for the reliability analysis of MSS. The direct partial logic derivatives reflect changing the value of investigation function when the values of its variables change. In [17] the new class of reliability indices was determined and was named dynamic reliabilityindices(DRI). The dynamic character of DRI consists to determine states of the system failure or, in other case, to the repair system is caused by a change of state the system component. In other words, these indices define the boundary states of MSS. In paper [21] three groups of DRI were obtained the dynamic reliability indices which define the boundary states of MSS are given and the conditions of being and changing of these states depending on the change of the system component states have been considered. However, these indices have high dimensionality and there are problems in their application for real-word engineering problems include three groups of probabilistic indices, [23]: Dynamic deterministic reliability indices (DDRI’s), component dynamic reliability indices (CDRI’s) and dynamic integrated reliability indices (DIRI’s). The DDRI’s evaluate an influence of a level change of a component state on system reliability. Numerical DDRI is defined as sets of the system states. These sets are calculated by direct partial logic derivatives. The CDRI’s allows measuring an influence of each individual component to the system reliability. The DIRI’s represent how change of one of system components impacts to the system reliability. But these indices permits to analyses the influence of one component state change to MSS reliability only.
In this paper we evolve an application of MSS reliability analysis methods for representation and estimation of system with “oil supply system”.

PROBLEM FORMULATION AND DESCRIPTION OF SYSTEM MODEL
image

DIRECT PARTIAL LOGIC DERIVATIVE FOR MSS MODEL
image

MULTI STATE SYSTEM FAILURE AND REPAIR OF MSS, [23]
Direct partial logic derivative of the structure function allows to examine the influence of the �� − ��ℎ component state change into the system reliability. In other words this derivative discovers the system states that are transformed as a result of the change of the component state.
Consequences of the direct partial logic derivatives are of interest for reliability analysis of the MSS for this purpose, consider the following two partial derivatives:
image
image
image
It is remarkable that direct partial logic derivatives allow to analyze dynamic properties of the MSS, which is submitted as structural function.

DYNAMIC RELIABILITY INDICES
Dynamic reliability indices characterize the change of the MSS reliability that is caused by the change of a component state and include three groups of probabilistic indices: dynamic deterministic reliability indices(DDRI’s), component dynamic reliability indices (CDRI’s) and dynamic integrated reliability indices (DIRI’s). Therefore, we will explain next each of these concepts in details.
image
image

ILLUSTRATIVE EXAMPLES
In this section, we shall study general example of MSS model for investigation of its dynamic behavior.

Example (1):
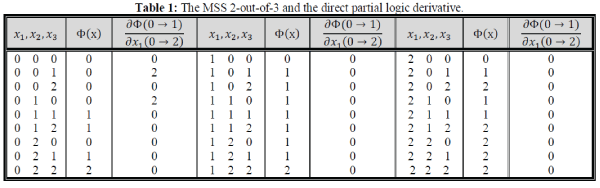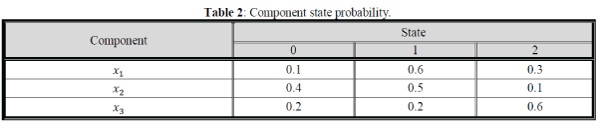image
image
image
image
We can calculate the CDRI for a 2-out-of-3 system which are presented in Table (3).
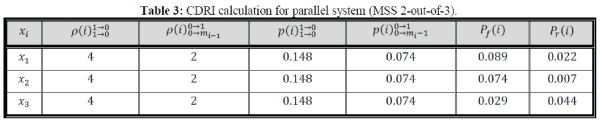image
image

DYNAMIC RELIABILITY OF OIL SUPPLY SYSTEM MODEL
Many engineering systems can fit into the proposed multi state system model. In this section, we will present on applications that have been identified by Tian, Z., Li, W. and Zuo, M. J., [15], Similar applications can be found in power supply systems and telecommunication systems.
Consider for example an oil supply system, as shown in Figure (1).
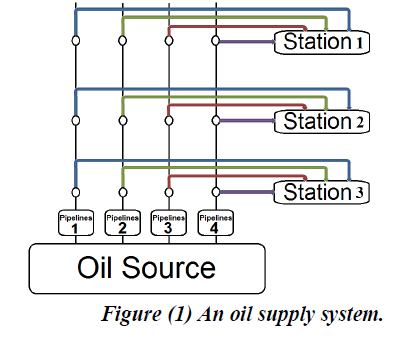image
image
1. State 0: oil cannot reach any stations.
2. State 1: oil can reach only station 1.
3. State 2: oil can reach station 1 and 2.
4. State 3: oil can reach station 1, 2 and 3.
Each station has different demands on the oil.
1. Station 1: requires at least one pipelines working to meet its demand.
2. Station 2: requires at least two pipelines working to meet its demand.
3. Station 3: requires at least four pipelines working to meet its demand.
At the system level, we are interested in whether the demands of up to a certain station can be met. Thus, four states of the oil supply system can be defined as follows:
1. System state 0: it cannot meet the oil demand of station 1.
2. System state 1: it can meet the oil demand of up to station 1. That is, the system can meet the demand of station 1, but cannot meet the demand of station 2.
3. System state 2: it can meet the oil demands of up to station 2. That is, the system can meet the demands of station 1 and station 2, but cannot meet the demand of station 3.
4. System state 3: it can meet the oil demands of up to station 3. That is, the demands of station 1, 2 and 3 can all be met.
In practice, we may be interested in the probability of the oil supply system in states 0, 1, 2 or 3.
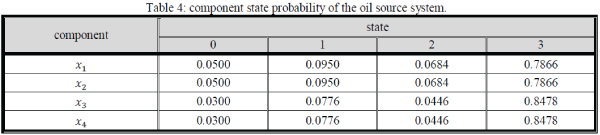
If ����, �� = 1,2,3,4 are used for the pipeline, then, the component state probability are given in table (4)
image
image
image
image

SIMULATION AND RESULTS
The results of the CDRI for the oil supply system are presented in Table (5).
image
image

CONCLUSION AND DISCUSSION
In this paper a new measure for MSS reliability is presented, which is calculated by using the structure function of MSS model for certain system network. This model allows to determine some level of system availability in contrast to the binary system. The MSS model is improved moreover: the system has a different number of discrete states for the system and for each component. This measure, which is labeled as DRI, involves the probabilities of the changes of the system states that are assigned by changes of component states. We consider two system changes: the system failure and system repair. But the suggesting method for reliability analysis of the MSS can be used to estimate the other changes in the system state. The dynamic reliability approach has been used successfully to evaluate the probability of the failure and repairing of the oil supply system as a real life application of dynamic multi-state k-out-of-n system model where the components and the system have multiple performance levels.All computational results are made by MATLAB program.

References
  1. Barlow, W. and Wu, A., “Coherent Systems With Multi-State Components”, Math. Oper. Res., Vol. 3, pp. 275–281, 1978.
  2. Block, H. and Savits T., “A Decomposition of Multi State Monotone System”, J. Appl. Prob., Vol. 19, pp. 391–402, 1982.
  3. Boedigheimer, R. A., “Customer-Driven Reliability Models for Multistate Coherent Systems”, Ph.D. Thesis, University of Oklahoma, Norman, 1992.
  4. El-Neweihi, E. and Proschan, F., “Degradable Systems: a Survey of Multistate System Theory”, Commun Stat Theory Methods, Vol. 13, pp. 405–432, 1984.
  5. El-Neweihi, E., Proschan, F. and Sethuraman, J., “Multi-State Coherent Systems”, J. Appl. Prob., Vol. 15 , pp. 675-688, 1978.
  6. Griffith, W. , “Multi-State Reliability models” J. Appl. Prob., vol. 17, pp. 735-744, 1980.
  7. Huang, J. and Zuo, M.J., “Generalized Multi-State k-out-of-n:G System”, IEEE Transactions on Reliability, Vol. 49 (1), pp. 105–111, 2000.
  8. Huang, J. and Zuo, M.J., “Multi-State k-out-of-n System Model and its Applications”, ProcIntSymp. on Annual Reliability and Maintainability, pp. 264-268, 2000.
  9. Lisnianski, A. and Levitin, G. “Multi-State System Reliability: Assessment, Optimization and Applications”, World Scientific, Singapore, 2003.
  10. Min, X., Yuan, S. D. and Kim, L. P, “Computing System Reliability Models and Analysis”. New York, Boston, Dordrecht, London, Moscow, 2004.
  11. Murchland, J., “Fundamental Concepts and Relations for Reliability Analysis of Multi-State Systems and Fault Tree Analysis,” in Theoretical and Applied Aspects of System Reliability, SIAM, pp. 581–618, 1975.
  12. Natvig, B., “Multi-State Coherent Systems”, in Encyclopedia of statistical sciences, Wiley, New York, Vol. 5.: pp. 732–735, 1985.
  13. Natvig, B., “Multi-State Reliability Theory”, In: Ruggeri F. Kenett, R. Faltinfw (eds) Encyclopediaof Statistics in Quality and Reliability, Wiley, New York, pp. 1160–1164, 2007.
  14. Ross, S. M., “Multivalued State Component Systems”, Annals of Probability, Vol. 7(2), pp.379–383, 1979.
  15. Tian, Z., Li, W. and Zuo, M. J., “Multi-State k-out-of-n Systems and their Performance Evaluation”, IIE Transactions, Vol. 41, pp. 32–44, 2009.
  16. Zaitseva, A. and Puuronen, S., “Multi-State System in Human Reliability”, IEEE Transactions on Reliability, Vol. 978(1), pp. 4244-3960, 2008.
  17. Zaitseva, E. and Levashenko, V, “New Dynamic Relia- bility Indices for Multi-State System”, Proc 3rd IntConf on Mathematical Methods in Reliability: Methodology and Practice, pp. 687-690, 2002.
  18. Zaitseva, E. and Levashenko, V., “Dynamic Reliability Indices for Parallel, Series and k-out-of-n Multi-State System”, in Proc. of the IEEE 52nd Annual Reliability & Maintainability Symposium (RAMS), pp.253 – 259, 2006.
  19. Zaitseva, E. and Levashenko, V., “Design of Dynamic Reliability Indices”, Proc IEEE 32th IntSymp on Multiple-Valued Logic, pp. 144-148, 2002.
  20. Zaitseva, E. and Levashenko, V., “New Reliability Indices for Multi-State System”, Proc 15th IEEE European Conf on Circuit Theory and Design, 345–349, 2001.
  21. Zaitseva, E., “Dynamic Reliability Indices for Multi-State System”, Journal of Dynamic System & Geometric Theories, Vol. 1 No. 2, pp. 213- 222, 2003.
  22. Zaitseva, E., “Reliability Analysis of Multi-State System, Dynamical Systems and Geometric Theories”, Vol. 1 (2), pp.213-222, 2003.
  23. Zaitseva, E., Levashenko, V. and Matiasko, K., “Reliability Analysis of Dynamic Behavior for Multi-State System”, Proc. Stochastic Models in Reliability, Safety, Security and Logistics Symp., (February), pp.386-389, 2005.