ISSN ONLINE(2320-9801) PRINT (2320-9798)
ISSN ONLINE(2320-9801) PRINT (2320-9798)
Subha S1, V.Murugan M.E., (Ph.D)2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering
This paper presents an enhancement of noisy reverberant speech signal by linear prediction analysis and spectral subtraction. The linear prediction analysis is used to suppress the short term reverberation. In general, the equalized impulse response has two detrimental effects, late impulses and pre-echo. These late impulses and pre-echo are suppressed by spectral subtraction. In LP analysis, the SNR value is improved and also the LP parameters are calculated accurately by flattering the spectral components.
Keywords |
| spectral subtraction, linear prediction analysis, short term reverberation, late impulses, pre-echo |
I. INTRODUCTION |
| SPEECH signals captured with a distant microphone exhibit reverberation due to reflections off the walls and objects in the room. The sound emanates from the source at 1100 feet per second and its strikes wall and reflected back at various angles. This blurs the temporal and spectral characteristics of the direct sound. In addition, the received signal is distorted by noise. As a consequence, reverberation and background noise degrade the perceived quality and intelligibility of the received speech signal, which causes serious difficulties in many applications such as hearing aids, hands-free teleconferencing, Automatic Speech Recognition (ASR), and scene analysis (source localization, tracking or identification). When a sound source is placed in closed room or near sound reflecting surfaces the listener receives not only the direct wave, but in addition multiple reflected waves. This smears the speech features and makes it less intelligible for humans and reduces the recognition rate for speech recognition engines. Therefore for best speech recognition results users are forced to use headsets with close-talk microphones. |
| There has been significant research on single microphone additive noise suppression algorithms, e.g., [2]. If the noise is negligible ,the speech enhancement task is just speech dereverberation. Bees et al. [3] employed a cepstrum based method to estimate the Room Impulse Response (RIR), and used a least squares technique for in version. Satisfactory results were only obtained for minimum phase or mixed phase responses with a few zeros outside the unit circle in the zplane, which restricts the use of this algorithm in real conditions. Unoki et al. [4] proposed the power envelope inverse filtering method, which is based on the Modulation Transfer Function (MTF), to recover the average envelope modulation spectrum of the original speech. However, this method has limited applicability due to the assumptions which do not necessarily match the features of real speech (real speech signals were not considered), and reverberation (a simple exponential model was employed for the RIR). Nakatani et al. [5] have shown that it is possible to accurately estimate the dereverberation filter for a Reverberation Time (RT60) up to 1 s. However, the method in [5] requires that the RIR remains constant for considerable time duration. Several researchers have considered only late reverberation suppression by assuming the early and late reverberant speech components are independent. The late reflection component is suppressed in the Short-Time Fourier Transform (STFT) domain using so-called spectral enhancement methods. This is achieved by estimating the Short-Term Power Spectral Density (STPSD) of the late reverberant speech component in order to perform magnitude subtraction without phase correction. Thus the main challenge is to estimate the STPSD of the late reverberant speech component from the received signal. More recently, a variety of techniques have been proposed to estimate the STPSD of the late reverberant speech component [6]–[12]. |
| Spectral subtraction is a commonly employed technique for dereverberation. It can be used in real-time applications, and results show a reduction in both additive noise and late reverberation. However, artifacts such as musicalnoise are introduced due to the nonlinear filtering, and a priori knowledge of the RIR (i.e., the reverberation time), is usually required. In this case, the blind reverberation time estimators are combined with spectral subtraction based approaches to perform complete blind dereverberation. Many spectral modification based approaches are robust against errors in reverberation time estimation as shown in [11]. Yegnanarayana and Murthy [13] proposed an LP residual based approach which identifies and manipulates the residual signal according to the regions of reverberant speech, namely, high Signal to Reverberation Ratio (SRR), low SRR, and reverberant signal only. This temporal domain method mainly enhances the speech specified features in the high SRR regions. In [14], the authors effectively combined a modified LP residual based approach (to enhance reverberant speech in the high SRR regions), with spectral subtraction to reduce late reverberation. |
| In this paper the linear prediction analysis and spectral subtraction is used to reduce the reverberation. the linear prediction analysis is used to filter the short time reverberation and the LP residual signal is obtained by LP analysis. That LP residual signal is given to the spectral subtraction section and the noise is reduced as shown in figure. |
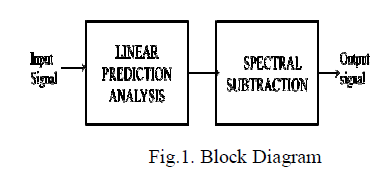 |
| Here linear prediction analysis is used to reduce the short term reverberation, which is discussed in next section, spectral subtraction of noisy speech, results and discussion are organized in other sections. |
II. LINEAR PREDICTION ANALYSIS |
| Linear prediction is a signal processing technique that is used extensively in the analysis of speech signals and, as it is so heavily referred to in speech processing literature, a certain level of familiarity with the topic is typically required by all speech processing engineers. This paper aims to provide a well-rounded introduction to linear prediction, and so doing, facilitate the understanding of the technique. Linear prediction and its mathematical derivation will be described, with a specific focus on applying the technique to speech signals. It is noted, however, that although progress in linear prediction has been driven primarily by speech research, it involves concepts that prove useful to digital signal processing in general. Linear prediction is a technique of time series analysis, that emerges from the examination of linear systems. Using linear prediction, the parameters of a such a system can be determined by analysing the systems inputs and outputs. Makhoul says that the method first appeared in a 1927 paper on sun-spot analysis, but has since been applied to problems in neurophysics, seismology as well as speech communication. |
| The pre-emphasis is the standard pre-processing step in speech processing. The pre-emphasis is used to improve the SNR of the speech signal by amplifying the signal. In speech processing, the original signal usually has too much lower frequency energy, and processing the signal to emphasize higher frequency energy is necessary. This is apparently a first order high pass filter. Pre-emphasis of the speech signal at higher frequencies has become a standard pre-processing step in many speech processing applications such as li near prediction (LP) analysis-synthesis and speech recognition . |
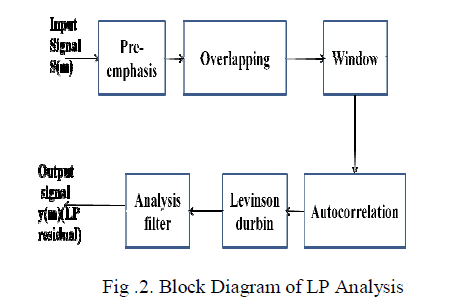 |
| For LP analysis-synthesis systems, pre-emphasis serves a useful purpose because, at the analysis stage, it reduces the dynamic range of the speech spectrum and this helps in estimating the LP parameters more accurately. Signals with higher modulation frequencies have lower SNR, In order to compensate this, the high frequency signals are emphasised or boosted in amplitude at the transmitter section of a communication system prior to the modulation process. That is, the pre emphasis network allows the high frequency modulating signal to modulate the carrier at higher level, this causes more frequency deviation. Generally, pre-emphasis is performed for flattening the magnitude spectrum and balancing the high and low frequency components. The point is that this task is defined based on the magnitude spectrum properties. Therefore, pre-emphasis appears not to be a much needed block in phase-based speech processing. Nevertheless, since the magnitude-based paradigms are prevailed in speech processing, even in the case of phase-based features, pre-emphasis is used, without any modification. |
| The signal is divided into number of frames of 320 samples and Overlapping the given input signal with 160 samples and buffered them. Whenever you do a finite Fourier transform, you're implicitly applying it to an infinitely repeating signal. So, for instance, if the start and end of your finite sample don't match then that will look just like a discontinuity in the signal, and show up as lots of high-frequency nonsense in the Fourier transform, which you don't really want. And if your sample happens to be a beautiful sinusoid but an integer number of periods don't happen to fit exactly into the finite sample, your FT will show appreciable energy in all sorts of places nowhere near the real frequency. You don't want any of that. |
| Windowing the data makes sure that the ends match up while keeping everything reasonably smooth; this greatly reduces the sort of "spectral leakage" described in the previous paragraph. The FT of a finite length segment of sinusoid convolves the Fourier transform of the window against the sinusoid's frequency peak, since a property of the FFT is that vector multiplication in one domain is convolution in the other. The FT of a rectangular window (which is what any unmodified finite length of samples in an FFT implies) is the messy looking Sinc function which splatters any signal that is not exactly periodic in the window over the entire frequency spectrum. The FT of a Hamming shaped window concentrates this "splatter" much nearer to the frequency peak after the convolution, resulting in a fatter but smoother frequency peak, but a lot less splatter across frequencies far from the frequency peak. This results in not only a cleaner looking spectrum, but also less interference from far away frequencies on any signal of interest. This interpretation (as opposed to the "infinitely repeating" interpretation) makes it more clear why differently shaped windows than Hamming may give you better results with even less "leakage". In particular, a Hamming window will reduce the size of the first Sinc side lobe of "leakage" right next to the frequency peak in exchange for actually more "leakage" (or convolution splatter) far from the frequency of interest. The idea of autocorrelation is to provide a measure of similarity between a signal and itself at a given lag. There are several ways to approach it, but for the purposes of pitch/tempo detection, you can think of it as a search procedure. In other words, you step through the signal sample-by-sample and perform a correlation between your reference window and the lagged window. The correlation at "lag 0" will be the global maximum because you're comparing the reference to a verbatim copy of itself. As you step forward, the correlation will necessarily decrease, but in the case of a periodic signal, at some point it will begin to increase again, then reach a local maximum. The distance between "lag 0" and that first peak gives you an estimate of your pitch/tempo. Twelfth-order autocorrelation coefficients are found, and then the reflection coefficients are calculated from the autocorrelation coefficients using the Levinson-Durbin algorithm. The original speech signal is passed through an analysis filter, which is an all-zero filter with coefficients as the reflection coefficients obtained above. The output of the filter is the residual signal. |
III. SPECTRAL SUBTRACTION |
| Spectral subtraction is a method for restoration of the power spectrum or the magnitude spectrum of a signal observed in additive noise, through subtraction of an estimate of the average noise spectrum from the noisy signal spectrum. The noise spectrum is usually estimated, and updated, from the periods when the signal is absent and only the noise is present. The assumption is that the noise is a stationary or a slowly varying process, and that the noise spectrum does not change significantly in between the update periods. For restoration of time-domain signals, an estimate of the instantaneous magnitude spectrum is combined with the phase of the noisy signal, and then transformed via an inverse discrete Fourier transform to the time domain. In terms of computational complexity, spectral subtraction is relatively inexpensive. However, owing to random variations of noise, spectral subtraction can result in negative estimates of the short-time magnitude or power spectrum. The magnitude and power spectrum are non-negative variables, and any negative estimates of these variables should be mapped into non-negative values. This nonlinear rectification process distorts the distribution of the restored signal. The processing distortion becomes more noticeable as the signal-to-noise ratio decreases. |
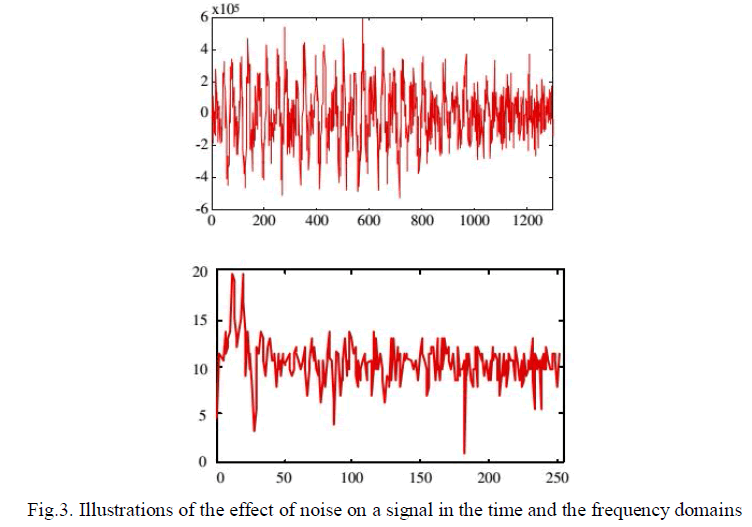
| In applications where, in addition to the noisy signal, the noise is accessible on a separate channel, it may be possible to retrieve the signal by subtracting an estimate of the noise from the noisy signal. However, in many applications, such as at the receiver of a noisy communication channel, the only signal that is available is the noisy signal. In these situations, it is not possible to cancel out the random noise, but it may be possible to reduce the average effects of the noise on the signal spectrum. The effect of additive noise on the magnitude spectrum of a signal is to increase the mean and the variance of the spectrum as illustrated in Figure. The increase in the variance of the signal spectrum results from the random fluctuations of the noise, and cannot be cancelled out. The increase in the mean of the signal spectrum can be removed by subtraction of an estimate of the mean of the noise spectrum from the noisy signal spectrum. The noisy signal model in the time domain is given by |
| y(m)= x(m) +n(m) (1) |
| where y(m), x(m) and n(m) are the signal, the additive noise and the noisy signal respectively, and m is the discrete time index.In the frequency domain, the noisy signal model of Equation is expressed as |
| Y( f )= X( f )+ N( f ) (2) |
| where Y(f), X(f) and N(f) are the Fourier transforms of the noisy signal y(m), the original signal x(m) and the noise n(m) respectively, and f is the frequency variable. In spectral subtraction, the incoming signal x(m) is buffered and divided into segments of N samples length. Each segment is windowed, using a Hanning or a Hamming window, and then transformed via discrete Fourier transform (DFT) to N spectral samples. |
| The windows alleviate the effects of the discontinuities at the end points of each segment. The windowed signal is given by |
| yw(m) = w(m)y(m) |
| = w(m)[x(m)+ n(m)] |
| = xw(m)+nw(m) (3) |
| The windowing operation can be expressed in the frequency domain as |
| Yw(f) =W(f)*Y (f) |
| =Xw(f)+Nw(f) (4) |
| where the operator * denotes convolution. Throughout this chapter, it is assumed that the signals are windowed, and hence for simplicity we drop the use of the subscript w for windowed signals. |
 |
| The equation describing spectral subtraction may be expressed as |
 |
 |
IV. CONCLUSION |
| In this paper we proposed a LP analysis and spectral subtraction for reduce the reverberation in the noisy speech signal. The LP analysis is mainly for producing the LP residual signal and suppresses the short term reverberation. The SNR value is improved by pre-emphasis. The LP residual signal is given to the spectral subtraction block and the long term reverberation is suppressed. After spectral subtraction the low region get over estimated, these over estimation of the low SNR region causes error. Further this error can be reduced by some reward punishment criteria’s. |
References |
|