Keywords
|
| secret sharing, information security, cryptography, multi-functionality |
INTRODUCTION
|
| A secret sharing scheme can secure a secret over multiple servers and remain recoverable despite multiple server failures. The dealer may act as several distinct participants, distributing the shares among the participants. Each share may be stored on a different server, but the dealer can recover the secret even if several servers break down as long as they can recover at least t shares; however, crackers that break into one server would still not know the secret as long as fewer than t shares are stored on each server. First threshold schemes were independently invented by both Adi Shamir [5] and George Blakely [6] in 1979. The definition outlined in [1] to describe what a threshold secret sharing scheme is: |
| Definition: |
| Let t and n be positive integers, t ≤ n. A (t, n) - threshold scheme is a method of sharing a key K among a set of n players (denoted by P), in such a way that any t participants can compute the value of K, but no group of t-1 participants can do so. The value of t is chosen by a special participant which is referred to by [1] as the dealer. When D wants to share the key K among the participants in P, gives each participant some partial information referred to earlier as a share. The shares should be distributed secretly, so no participant knows the share given to any other participant. Some of the threshold based SSS schemes are explained in the further sections. |
RELATED WORK
|
Shamir’s secret sharing
|
| Shamir secret sharing is based on polynomial interpolation over a finite field. Shamir developed the idea of a (t, n) threshold-based secret sharing technique (t ≤ n). The technique allows a polynomial function of order (t −1) constructed as, f(x) = d0 + d1x1 + d2x2 + . . . + dt−1xt−1 (mod p), where the value d0 is the secret and p is a prime number. The secret shares are the pairs of values (xi, yi), where yi = f(xi), 1 ≤ i ≤ n and 0 < x1< x2 . . < xn ≤ p − 1. |
| The polynomial function f(x) is destroyed after each shareholder possesses a pair of values (xi, yi) so that no single shareholder knows the secret value d0. In fact, no groups of t − 1 or fewer secret shares can discover the secret d0. On the other hand, when t or more secret shares are available, then we may set at least t linear equations yi = f (xi) for the unknown di’s. The unique solution to these equations shows that the secret value d0 can be easily obtained by using Lagrange interpolation. |
| Some of the useful properties of Shamir's (k,n)threshold scheme are: |
| 1. Secure: Information theoretic security. |
| 2. Minimal: The size of each piece does not exceed the size of the original data. |
| 3. Extensible: When k is kept fixed, Di pieces can be dynamically added or deleted without affecting the other pieces. |
| 4. Dynamic: Security can be easily enhanced without changing the secret, but by changing the polynomial occasionally (keeping the same free term) and constructing new shares to the participants. |
| 5. Flexible: In organizations where hierarchy is important, we can supply each participant different number of pieces according to their importance inside the organization. For instance, the president can unlock the safe alone, whereas 3 secretaries are required together to unlock it. |
Blakley’s secret sharing scheme [5]:
|
| Blakleys SSS uses hyper plane geometry to solve the secret sharing problem. To implement a (t, n) threshold scheme, each of the n users is given a hyper-plane equation in a t dimensional space over a finite field such that each hyper plane passes through a certain point. The intersection point of the hyper planes is the secret. When t users come together, they can solve the system of equations to find the secret. The secret is a point in a t dimensional space and n shares are affine hyper planes that pass through this point. An affine hyperplane in a t-dimensional space with coordinates in a field F can be described by a linear equation of the following form: |
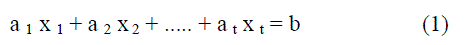 |
| Reconstruction of original secret is simply finding the solution of a linear system of equations. The intersection point is obtained by finding the inter-section of any t of these hyper planes. The secret can be any of the coordinates of the intersection point or any function of the coordinates. |
Li bai’s secret sharing:
|
| Li Bai developed a threshold secret sharing based upon the invariance property of matrix projection. The scheme is divided in two phases: |
| Construction of Secret Shares from Secret Matrix S |
| 1. Construct a random m × k matrix A of rank k where |
| 2. m > 2(k - 1) – 1. |
| 3. Choose n linearly independent k×1 random vectors xi. |
| 4. Calculate share vi = (A×xi) (mod p) for 1≤ i ≤ n, where p is a prime number. |
| 5. Compute $ = (A (A’A)-1A’) (mod p). |
| 6. Solve R = (S - $) (mod p). |
| 7. Destroy matrix A, xi’s, $, S and |
| 8. Distribute n shares vi to n participants and make matrix R publicly known. |
| Secret Reconstruction |
| 1. Collect k shares from any k participants, say the shares are v1, v2, . . . ., vk and construct a matrix B ={v1 v2 . . . vk}. |
| 2. Calculate the projection matrix $ =(B (B’B)-1B’) (mod p). |
| 3. Compute the secret S = ($ + R (mod p)). |
COMPARATIVE STUDY
|
| The proposed scheme is compared with existing Threshold Secret Sharing Schemes like Shamir’s Secret Sharing, Blakley’s Secret Sharing and Li Bai’s Secret Sharing. |
| The above table shows the comparative study of the existing secret sharing schemes |
CONCLUSION
|
| In this paper we have done a review of the existing threshold based secret sharing schemes and performed a comparative study on the secret sharing schemes. Table I shows comparison of the secret sharing schemes with respect to various parameters. |
| |
Tables at a glance
|
 |
| Table 1 |
|
| |
References
|
- Sonali Patil,Prashant Deshmukh, “A Novel (t, n) Threshold Secret Sharing Using Dot Product of Linearly Independent Vectors.”, International Journal of Advanced Research in Computer and
- Communication Engineering Vol. 2,Issue ,7 July 2013.
- S.Jaya Nirmala , S.Mary Saira Bhanu , Ahtesham Akhtar Patel,” Comparative Study Of Secret Sharing Algorithms For Secure Data in the Cloud”, International Journal on Cloud Computing: Services and Architecture(IJCCSA),Vol.2, No.4, August 2012.
- Md Kausar Alam, Sharmila Banu K, “An Approach to Secret Sharing Algorithm in Cloud Computing Security over Single to Multi Clouds”, International Journal of Scientific and Research and Research Publication, Volume 3, Issue 4, April 2013.
- Cheng Gu, and Chin-Chen Chang,“ A Construction for Secret Sharing Scheme with General Access Structure” , Journal of Information Hiding and Multimedia Signal Processing Ubiquitous International Volume 4, Number 1, January 2013 2013 ISSN 2073-4212
- Sonali Patil, Prashant Deshmukh, “ An Explication of Multifarious Secret Sharing Schemes”, International Journal of Computer Applications(0975 – 8887) Volume 46– No.19, May 2012
- Sonali Patil, Prashant Deshmukh, “Analyzing Relation in Application Semantics and Extended Capabilities for Secret Sharing Schemes” IJCSI International Journal of Computer Science Issues, Vol. 9, Issue 3, No 1, May 2012 ISSN (Online): 1694-0814
- Sonali Patil, Kapil Tajane, Janhavi Sirdeshpande, “An explication of secret sharing schemes with general access structure” International Journal of Advances in Engineering & Technology, May 2013. ISSN: 2231-1963
- Atanu Basu, Indranil Sengupta and Jamuna Kanta Sing, “Cryptosystem for Secret Sharing Scheme with Hierarchical Groups” International Journal of Network Security, Vol.15, No.6, PP.455-464, Nov. 2013
|