Watermarking is an effective technology that solves many problems within a digitization project. A high capacity data entrenching scheme based on precise and fast framework for the computation of Zernike moments (ZMs) is proposed in this paper. The high capacity is achieved by maximizing data entrenching size and improving the hiding ratio after dipping the inaccuracies in the computation of ZMs. Furthermore, a concept of conditional quantization technique which enables to reduce the total number of ZMs needed to be modified during watermark embedding. Conditional quantization technique concept enhances the visual imperceptibility of the watermarked image and its robustness against various at tacks.
INTRODUCTION |
| The rapid expansion of the internet in the past years has rapidly increased the availability of digital data such as audio,
images and videos to the public. By embedding Intellectual Property data (e.g. the creator, licence model, creation date
or other copyright information) within the digital object, the digitiser can demonstrate they are the creator and
disseminate this information with every copy, even when the digital object has been uploaded to a third party site. It
can also be used to determine if a work has been tampered with or copied. Embedding capacity of a watermarking
scheme refers to the amount of information that can be embedded without significant loss of the quality of
watermarked images. Only a few techniques provide high-capacity data embedding as increasing capacity adversely
affects the visual imperceptibility and watermark robustness to various attacks. |
RELATED WORK |
| As we have witnessed in the past few months, the problem [1], [2] of protecting multimedia information becomes more
and more important and a lot of copyright owners are concerned about protecting any illegal duplication of their data or
work. An effective image watermarking scheme must satisfy some basic requirements such as watermark robustness,
embedding capacity, visual imperceptibility, uniqueness and minimum computational load for embedding or detecting
the watermark. Geometrically robust image watermarking using moment invariants was introduced by Alghoneimy and
Tewfik [3].However, the instability because of non-linear nature of the invariants and difficulty in embedding multi-bit
watermark restrict its usability for informative watermarking. Since then, numerous invariant watermarking schemes
have been designed using different moment families such as Fourier–Mellin moments [4], complex moments [5],
wavelet moments [6], Zernike and pseudo-Zernike moments (ZMs/PZMs). Among these, ZMs are considered the most
suitable for invariant watermarking because of minimum information redundancy and better immunity to noise. Farzam
and Shirani [7] used ZMs for designing a watermark scheme that provides good watermark robustness against rotation,
additive noise and JPEG compression. Their approach, however, suffers from high computational complexity and poor
reconstruction quality because of inverse Zernike transform. Later, Kim and Lee [8] proposed a method to embed the
zero-bit watermark signal by constructing a feature vector consisting of some low-order ZMs (up to order 5) and
directly adding orthogonal patterns in spatial domain to avoid fidelity degradation. The first well-designed and
complete geometrically invariant watermarking scheme using ZMs/PZMs was given by Xinet al. [9]. They embed a multi-bit watermark signal by quantising the magnitudes of selected moments using dither modulation. By exploiting
the linearity in image reconstruction process, actual embedding is done in the spatial domain to obtain high
imperceptibility. |
| A recent study on the performance evaluation of moment-based watermarking methods [10] reveals that ZMs-based
methods are among the most suitable candidates for high-capacity image watermarking. The existing methods for the
computation of ZMs, however, prohibit their usage for high-capacity data embedding because of certain drawbacks.
First, the computation of ZMs suffers from geometric and numerical integration errors. As a consequence of these
errors and the digital nature of image function, some ZMs with order p and repetition q, Zpq, with q = 4m, m ‘integer’,
are computed more inaccurately than others [9]. This restricts the use of approximately one fourth of the total number
of moments for image watermarking. Second, moment orders higher than 44 become inaccurate because of instability
in their computation [11]. This restricts the embedding capacity to 385 bits. Third, the time complexity of ZMs
computation is very high which is a major limiting factor for high moment orders and large image sizes. The
inaccuracies in the moment computation not only limit capacity, but also affect robustness and imperceptibility. An
attempt is made by Ismail et al. [12] to enhance the robustness and imperceptibility of watermark embedding by
adopting an accurate computational framework for ZMs in polar domain [13]. However, the inaccuracy in moment
computation persists for moment order > 44 because of numerical instability. Moreover, the accurate computation of
ZMs in polar domain requires reconfiguration of square pixel grids into circular grids and interpolation of image
intensity values at new pixel locations. The interpolation process adds to the computation burden. Moreover, it
introduces interpolation error, although the magnitude of interpolation error is much less than the errors when moments
are computed in the Cartesian domain. The problem of numerical instability at high orders still exists. |
| Using fast computation of ZMs, robust, imperceptible and high-capacity image watermarking methods are formed. A
novel bit embedding method using dither modulation based on conditional quantisation is proposed. The proposed bit
embedding method not only enhances the visual imperceptibility of the watermarked images, but also improves the
watermark robustness to various attacks. Exhaustive experimental analysis is performed for high capacity, robustness
to various geometric and image processing attacks and improved visual imperceptibility of watermarked images. |
PROPOSED COMPUTATION |
| Simply the projection of the image function onto the orthogonal basis functions is known as Zernike moments. This
orthogonally enables us to determine the individual contribution of each order moment. The Zernike moments Zpq, of
order p and repetition q for a two-dimensional continuous image function, f(x, y), over a unit disk in the Cartesian
domain are given by |
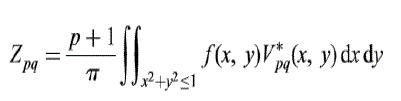 |
| One of the major properties of ZMs is that if all moments Zpq of an image function f (i, k) up to maximum order
pmax are known, then it is possible to reconstruct the image using the inverse transformation equation as follows |
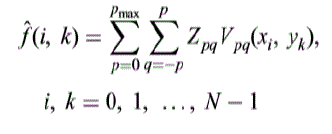 |
| The proposed ZMs computational method requires n × n number of computations over a pixel area of the kernel
function, thus making the overall complexity of ZMs computation of the order O _ n2N 2p3max . This may be a limiting
factor for watermarking applications requiring high order of moments or large image sizes. Fortunately, there exist a
number of methods that significantly enhance the speed of ZMs computations. These methods are generally based on
the recurrence relations for the Zernike polynomials and the 8-way symmetry and anti-symmetry properties of their kernel functions. The use of recursive algorithms reduces the time complexity of radial polynomials from quadratic
order O _ p2max to linear order O (pmax). Furthermore, speed enhancement can be achieved by using recursive
relations for the computation of trigonometric terms involved in the angular function e−jqθ without the involvement of
library functions (which are more computation intensive). |
SYSTEM DESIGN |
| For accurate and fast computation of ZMs, an image adaptive procedure is developed that enhances the visual
imperceptibility and watermark robustness by reducing the number of moments to be modified during embedding. The
general structure of the proposed embedding procedure and decomposition procedure is depicted in Fig. 1. To embed
the given watermark bit sequence B = {bi ∈ {0, 1}, i = 1, 2,……..L}, L number of ZMs are selected randomly using
some secrete key K and the ZMs are computed accurately using the proposed computation framework to form the
Zernike feature vector of size L. |
Selection of ZMs |
| Accuracy in the computation of ZMs makes all moments usable for image watermarking. However, taking into account
only magnitude independent moments we define S = {Zpq, 0 < p ≤ pmax, |q| ≤ p} as a set of all Zpq that can be used
for watermarking. Z00 is excluded as it represents the average intensity. Depending on the length of watermark bit
sequence L, a number of ZMs are selected from set S using some secret key K to enhance the security of watermarking
and rm the feature vector Z = Zp1, q1, Zp2, q2 ,..., ZpL ,qL. A very effective quantisation technique which enhances
the visual imperceptibility and watermark robustness of the watermarked image by reducing the number of ZMs
needed to be modified during embedding. For this purpose, the magnitude of each selected ZMs |Zpi , qi| is
quantised with two dither functions di(0) and di(1) to compute |Z0pi , q| and |Z1pi , qi|, respectively, using un-coded
binary dither modulation as follows |
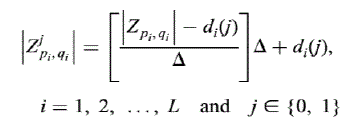 |
| If all ai = bi then no ZMs are modified and there is no quality degradation of the watermarked image. In such a case,
watermark sequence B becomes an adaptive signal generated from the magnitudes of selected ZMs. The worst-case
performance of the proposed scheme is bounded by the existing scheme [13] when all selected moments need to be
quantized. However, as the quantize di (·) follows uniform distribution over the interval [0, Δ/2], statistically half of the
bits to be embedded should match with their corresponding conditional bits. Thus, we observe that on average half of
the selected ZMs will remain unmodified during the embedding process because of the proposed quantization
technique resulting in better visual imperceptibility of the watermarked image. |
Reconstructing spatial signal and watermark Embedding |
| The watermark signal is added into the intensity of the image after reconstructing the spatial signal using elected ZMs
kernel functions. If a bit bi modifies the moment Zpi , qi of the original image by an amount 1pi , qi which is referred
to as quantized noise signal, then the total contribution of L modifications as intensity pixel value can be computed as
follows |
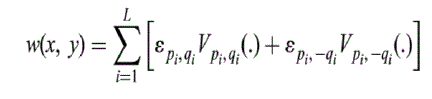 |
| Where, |
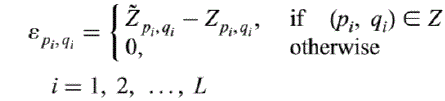 |
| As |Vpiqi| = |Vpi, −qi| ≤ 1, the distortion added to the image is bounded by w(x, y) ≤ 2 Li=1|Σ pi, qi|. Therefore |Σ pi,
qi| controls the maximum pixel distortion in the image. Clearly, the amount of distortion depends on the matching ratio
of ai with bi with higher matching ratio providing smaller deviation in intensity resulting in better visual
imperceptibility. The final watermarked image fwat(x, y) is formed as
fwat(x, y) = f (x, y) + w(x, y) |
Watermark extraction |
| The process of extraction is similar to generating conditional bits from selected ZMs. The ZMs feature vector Z′ =
{Z′p1, q1, Z′p2, q2, . . . , Z′pL, ql} is computed from the possibly attacked watermarked image f ′wat(x, y). The
magnitude of each Z′pi , qi is re-quantized with both dither functions di(0) and di(1) to compute |Z′0pi , qi| and |Z′1pi ,
qi|, respectively, as in (12) and the minimum distance decoder of (13) is used to estimate the bit sequence ˆB = kˆb1,
ˆb2, . . . , ˆbLl embedded in the received image. |
| The embedding capacity of a watermarking scheme is measured using data hiding ratio (DHR) which is the ratio
between the maximum data embedding size and the original uncompressed host media size. Clearly, the DHR is
directly related to the cardinality of set S representing the maximum number of magnitude independent moments that
can be computed accurately and are usable for data hiding. The proposed accurate computation method increases the
maximum data embedding size by making all ZMs including q = 4m, accurate and useful for data embedding. |
| Another factor affecting the embedding capacity of the ZMs-based watermarking scheme is the maximum order up to
which moments can be computed accurately without exhibiting numerical instability. The fact that numerical instability
affects the embedding capacity of a watermarking system can be observed through bit error rate (BER). The value of
BER lies between 0 and 1 with values of BER ≥0.25 signifying that more than one fourth of the bits extracted are
incorrect and presumably there is failure to extract the watermark. The maximum embedding capacity for the method
of Xin et al. [13] is 385 and for the method of Li et al. [14] it is 475. It is worth mentioning here that an average BER ≈ 0.5 is obtained using ZOA computation method as statistically about 50% of the bits extracted turn out to be correct
because of random behaviour of the bit sequence. The maximum value of pmax = 150 is taken arbitrarily although
higher values of pmax can also be taken [15]. |
Watermark robustness against various attacks |
| During rotation, the intensity values are changed because of interpolation process and these values deviate marginally
from the original ones. The deviation with respect to the angle of rotation does not have a specific trend. Owing to 8-
way symmetry/anti-symmetry properties, rotations beyond 45° will produce identical trends. The values of BER varies
with respect to rotation angle, because of various discretization errors the magnitude of ZMs are not truly invariant
against rotation. The accurate computation of ZMs improves the rotation invariance property of the moments [24]. The
proposed methods provide lower values of average BER compared with the existing approaches. Similar results for
scaling attack also. When computed using ZOA method, PSTs provide better robustness than ZMs-based watermarking
method [9]. However the accuracy in the computation of ZMs improves the magnitude invariance of moments against
scaling [15] thereby providing better watermark robustness against scaling attacks. Further, it enhances watermark
robustness as the improved magnitude invariance properties are better preserved, resulting in smaller values of BER
compared with other methods for all rotation angles and scaling factors. |
Time complexity |
| With the use of fast computation framework, the time requirement can be reduced considerably and for all moments the
value of the CPU elapse time for pmax = 35 is only 1.717 s for the proposed method with considerably better
performance compared with 2.781 s for the existing approach with lower performance. The computation of PSTs takes
much less time as compared with ZMs because of its less computation intensive kernel function. The CPU elapse time
for computing all transform coefficients with order and repetition pmax = qmax = 35 is 0.349 s only. |
CONCLUSION |
| Fast computational framework for the calculation of ZMs helps to improve the robustness and secured watermarking. A
novel image adaptive embedding method is also proposed that reduces the number of ZMs to be modified. The
proposed method provides better invariance properties of the ZMs resulting in improved visual imperceptibility and
watermark robustness. The method is, however, computation intensive thus resulting in increased time requirement.
The time requirement is reduced by the use of recursive methods for the computation of Zernike radial and angular
functions and their 8-way symmetry/anti-symmetry property. These methods not only provide the better speed, but also
provide numerical stability to high order of moments which are required for high embedding capacity. Thus, the
proposed framework turns out to be more suitable for embedding large number of bits in high-capacity image
watermarking applications with more security. |
| |
Figures at a glance |
 |
| Figure 1 |
|
| |
References |
- P. Ruotsalainen, “Privacy and security in teleradiology,” Eur. J. Radiol., vol. 73, pp. 31–35, 2010.
- F. Prior, M. L. Ingeholm, B. A. Levine, and L. Tarbox, “Potential impact of HITECH security regulations on medical imaging,” in Proc. Eur.Molecular Biol. Conf., 2009, pp. 2157–2160
- Alghoniemy, M., Tewfik, A.H.:‘Image watermarking by moment invariants’. Proc. IEEE Int. Conf. Image Processing, 10–13 September 2000, pp. 73–76
- Lin, C.Y., Wu, M., Bloom, J.A., Cox, I.J., Miller, M.L., Liu, Y.M.:‘Rotation, scale, and translation resilient watermarking for images’, IEEE Trans. Image Process., 2001, 10, (5), pp. 767–782.
- Zhu, H., Liu, M., Li, Y.:‘The RST invariant digital image watermarking using Radon transform and complex moments’, Digit. Signal Process., 2010, 20, pp. 1612–1628
- Wang, X.Y., Yang, Y.P., Yang, H.Y.:‘Invariant image watermarking using multi-scale Harris detector and wavelet moments, Comput.Electr. Eng., 2010, 36, (1), pp. 31–44
- Farzam, M., Shirani, S.:‘A robust multimedia watermarking technique using Zernike transform. Proc. IEEE Fourth Workshop on Multimedia Signal Processing, 3–5 October 2001, pp. 529–534
- Kim, H.S., Lee, H.-K.:‘Invariant image watermark using Zernike moments’, IEEE Trans. Circuits Syst. Video Technol., 2003, 13, (8), pp. 766– 775
- Xin, Y., Liao, S., Pawlak, M.:‘Circularly orthogonal moments for geometrically robust image watermarking’, Pattern Recognit., 2007, 40, (12),pp. 3740–3752
- Tsougenis, E.D., Papakostas, G.A., Koulouriotis, D.E., Tourassis, V.D.: ‘Performance evaluation of moment-based watermarking methods: a review’, J. Syst. Softw., 2012, 85, (8), pp. 1864–1884
- Singh, C., Walia, E.: ‘Algorithms for fast computation of Zernike moments and their numerical stability’, Image Vis. Comput., 2011, 29, (4), pp. 251–259
- Ismail, I.A., Shouman, M.A., Hosny, K.M., Abdel Salam, H.M.: ‘Invariant image watermarking using accurate zernike moments’, J. Comput. Sci., 2010, 6, (1), pp. 52–59
- Xin, Y., Pawlak, M., Liao, S.: ‘Accurate computation of Zernike moments in Polar coordinates’, IEEE Trans. Image Process., 2007, 16, pp. 581–587
- Li, L., Li, S., Abraham, A., Pan, J.-S.: ‘Geometrically invariant image watermarking using polar harmonic transforms’, Inf. Sci., 2012, 199, pp. 1–19
- Singh, C., Upneja, R.: ‘Fast and accurate method for high order Zernike moments computation’, J. Appl. Math. Comput., 2012, 218, pp. 7759– 7773
|