ISSN ONLINE(2320-9801) PRINT (2320-9798)
ISSN ONLINE(2320-9801) PRINT (2320-9798)
S.Hemalatha, Dr.R.Manickachezian
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering
Cloud computing is an emerging technology that is still uncertain to many security problems. Ensuring the security of stored data in cloud servers is one of the most challenging issues in such environments. RSA provide secure transmission over transmission channel. Main advantage of RSA is prime factorization. With the ever increasing number of connected devices and the over abundance of data generated by these devices, data privacy has become a critical concern in the Internet of Things. One promising privacy-preservation approach is Attribute-Based Encryption (ABE), a public key encryption scheme that enables fine-grained access control, scalable key management and flexible data distribution. The main aim of this exertion is to discuss the security strength of RSA and Attribute based encryption (ABE).
Keywords |
| Attribute Based Encryption, RSA, Security Strength, Prime factorization. |
INTRODUCTION |
| Cloud Computing is the key driving power in many small, medium and large sized companies and as many cloud users seek the services of cloud computing, the major concern is the security of their data in the cloud. Securing data is always of vital importance and because of the critical nature of cloud computing and the large amounts of complex data it carries, the need is even more important. Hence forth, concerns regarding data privacy and security are proving to be a barrier to the broader uptake of cloud computing services. |
| As many companies move their data to the cloud the data undergoes many changes and there are many challenges to overcome. To be effective, cloud data security depends on more than simply applying appropriate data security procedures and counter measures. Computer based security measures mostly capitalizes on user authorization and authentication. In traditional encryption schemes, a sender usually needs to know the identities of the intended recipients and needs to pre-share credentials with them. The objective is that a sender encrypts data that can only be decrypted and read by an exact recipient. Given its exclusive benefits, ABE has recently gained much attention and has been adopted by many cloud computing applications and large-scale dynamic systems. Attribute-based encryption (ABE) [6] is an expansion of public key encryption that allows users to encrypt and decrypt messages based on user attributes. |
| The well-known RSA algorithm is very strong and useful in many applications. But it is not used so often in smart cards for its big computational cost. The rest of the paper is summarised as follows. The section II discusses about the related work based on RSA and ABE. In section III and IV , the algorithms of RSA and ABE are examined. The security strengths of RSA and ABE are discussed under section V and VI. The SectionVII states the results and discussions. Finally the work is concluded in section VIII. |
RELATED WORK |
| In cloud environments, if a data owner wants to share data with users, he will encrypt data and then upload to cloud storage [13] service. Through the encryption step, the cloud cannot know the information of the encrypted data. Besides, to avoid the unauthorized user accessing the encrypted data in the cloud, a data owner uses the encryption scheme for access control of encrypted data. In existing schemes, many encryption schemes can achieve and provide security, assure data confidential, and prevent collusion attack scheme. One of the encryption schemes is attributebased encryption scheme. The first concept of attribute-based encryption was proposed in 2005.Attribute-Based Encryption (ABE) was first proposed by A. Sahai and B. Waters [2] with the name of Fuzzy Identity-Based Encryption, with the original goal of providing an error-tolerant identity-based encryption scheme that uses biometric identities. V. Goyal, O. Pandey, A. Sahai, and B. Waters enhanced the original ABE scheme by embedding a monotone access structure into user secret key. The scheme is called Key-Policy Attribute-Based Encryption (KP-ABE) [1], a variant of ABE. They also proposed the concept of Ciphertext- Policy Attribute Based Encryption (CP-ABE) without presenting a concrete construction. |
| The RSA Factoring Challenge was started in March 1991 by RSA Data Security to keep abreast of the state of the art in factoring. Since its inception, well over a thousand numbers have been factored, with the factors returning valuable information on the methods they used to complete the factorizations. The Factoring Challenge provides one of the largest test-beds for factoring implementations and provides one of the largest collections of factoring results from many different experts worldwide. |
THE RSA ALGORITHM |
| The most commonly used asymmetric algorithm is Rivest-Shamir-Adleman (RSA)[7]. It was introduced by its three inventors, Ronald Rivest, Adi Shamir and Leonard Adleman in 1977. It is mostly used in key distribution and digital signature processes. RSA is based on a one-way function in number theory, called “integer factorisation”. A one-way function is a function, which is “easy” to compute one way, but “hard” to compute the inverse of it. Here easy and hard should be understood with regard to computational complexity, especially in terms of polynomial time problems. |
| RSA Cryptosystem: The original RSA algorithm was publicly illustrated in 1977 [3] and after that many related algorithms were projected based of original RSA in order to set right the flaw of the basic algorithm. The Original RSA scheme is as follows: |
A. Key Generation Algorithm |
| Step1: Randomly and secretly choose two large primes: p, q and compute n = p. q |
| Step2: Compute ÃÂÃ⢠(n) = (p – 1) ( q – 1) . |
| Step3: Select Random Integer: e such as 1 < e < n and gcd (e, ÃÂÃâ¢) = 1. |
| Step4: Compute d such as e. d ≡ 1 mod ÃÂÃâ¢(n) and 1 < d < ÃÂÃ⢠(n) . |
| Step5: Public Key: (e,n) |
| Step6: Private Key: (d,n). |
B. Encryption process |
| Step1: Suppose entity R needs to send message m to entity S (represent m as an integer in the range of 0 < m<n). |
| Step2: Entity S should send his public key to entity R. |
| Step3: Entity R will encrypt m as c = me mod n and will send c to entity S. |
C. Decryption Process |
| Step1: Entity S will decrypt the received message as m = cd mod n. |
| The most important advantage of RSA[15] is ensuring about the privacy of the private key because this key will not be transmitted or revealed to another user. However, this algorithm has some considerable weaknesses. The main computational costs of the RSA are the modular exponentiations found during the key generation, encryption and decryption process [4]. Moreover, this algorithm has some weaknesses against certain attacks (i.e., Brute force, Mathematical attacks, Timing attacks and Chosen Cipher-text attacks) [5]. To reduce these problems, many algorithms have been designed and introduced based on original RSA. The most popular algorithms identified for improving the main algorithm are RSA Small-e and Efficient RSA. |
ATTRIBUTE-BASED ENCRYPTION SCHEME |
| An Attribute Based Encryption system usually consists of a key authority, senders and recipients. The key authority substantiate senders and recipients, generates public/private keys, and issues the keys to senders and recipients. The four major algorithms in ABE are Setup, KeyGen, Encryption and Decryption. During the Setup stage, the key control generates a pair of public key and master secret key based on limit initialized from pairing-based cryptography [8], [9]. It keeps the master secret key and distributes the public key to each end user in the system. The key authority then runs the KeyGen algorithm to generate subscribers’ private keys per demand. The Encryption and the Decryption algorithms are executed by senders and recipients respectively. An ABE scheme consists of four main algorithms as described below |
| Step1: Setup(κ, U). The input limits of this algorithm are the security parameter κ and the universe of attribute U. The primitive create a master key MK along with the domain parameters PK. |
| Step2: Encryption(PK,M,A). The set of domain parameters PK, the message M and the access policy A specified as a boolean formula whose operands are a subset of the universe of attributes are taken as the input for this algorithm. Then, this algorithm encrypts M as the ciphertext CT in such a way that only those user who has the set of attributes required to satisfy the access policy A, will be able to decrypt it. It is assumed that the ciphertext and the access policy A must be transmitted together as a pair. |
| Step3: Key generation(MK,S). The master key MK along with a set of attributes S are taken as the input in this algorithm. Then, the private key SK is generated with the prescribed set of attributes. Usually, this primitive is executed by a “trusted third party” that has the vital role of generating private key for each one of the participants with a specific access privileges. |
| Step4: Decryption(PK,CT,SK). This primitive takes as input the domain parameters PK along with the ciphertext CT and its corresponding access policy A, and the private key SK, which contains the set of attributes S. Only in the case that the set of attributes S satisfies the policy A, this primitive will be able to recover the message M from the ciphertext CT. |
| A. Features of Attribute Based Encryption |
| The two main features of attribute based encryption are given below: |
| The complex access control policies can be addressed. |
| The exact list of users need not be known appropriately. Knowledge of the access policy is sufficient. |
| B. Types of Security Levels |
| In common there are four security levels to secure the data in cloud computing. Each level has own database and consists of many sets. These levels and the key length are mentioned in the below Table 1. |
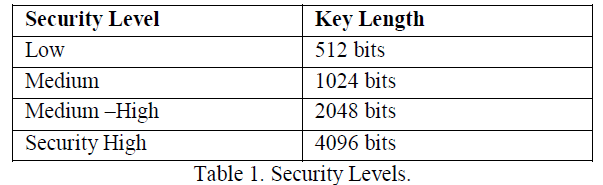 |
| The users must select the same security level or change the security level before starting the encryption and decryption processes. |
SECURITY STRENGTH OF RSA |
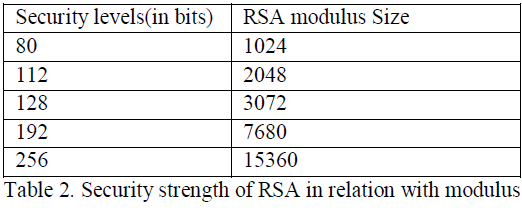
| Cryptographic algorithms provide various “strengths” of security, depending on the algorithm and the key size used. In this discussion, the algorithms are considered and compared the strength for the given key sizes. If the amount of task needed to “smash the algorithms” or establish the keys [14] is approximately the same using a given resource. The security strength of an algorithm for a given key size is conventionally described in terms of the quantity of work it takes to try all keys for a symmetric algorithm with a key size of "X" that has no short cut attacks (i.e., the most efficient attack is to try all possible keys). In this case, the best attack is said to be the fatigue attack. An algorithm that has a Y-bit key, but whose strength is equivalent to an X-bit key of such a symmetric algorithm is said have a “security strength of X bits” or to provide “X bits of security” based on Integer Factorization Cryptography. |
 |
SECURITY STRENGTH OF ABE |
| As one can imagine, stronger security requires longer primitives in cryptographic computations, which acquire more overhead. To measure the correlation between security level and performance, here the security levels which ABE offers and what determines the ABE security level are examined. Because ABE is built on top of pairingbased cryptography, its security strength is determined by the underlying pairing based cryptographic algorithm, which in turn is determined by the bit-length of the parameters [8], [9]. Suppose E is the underlying elliptic curve used by the pairing algorithm, and E is defined over a finite field Fq. The parameters that determine the security strength of the pairing include the field size q and the prime order r of the base-point P ∈ (Fq) (r does not divide q) as well as the embedding degree k, which is the multiplicative order of q modulo r. Type A pairing in the jPBC library [14] which has a fixed k = 2 [9] based on pairing based cryptographic algorithm is used here. |
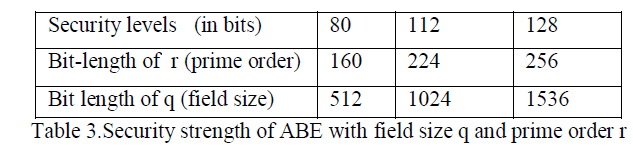 |
| It is considered one of the most efficient pairing algorithms available in the jPBC library[10]. Therefore, the two parameters that can be adjusted to achieve different security levels are r and q. According to [8] and [11], with a fixed k = 2, the bit-length choices of r and q and their equivalent security levels in terms of symmetric key encryption and RSA are summarized in the above table. Starting with the 80-bit security level, which is sufficient for most medium-security purposes [12], here three common security levels are compared. |
RESULTS AND DISCUSSIONS |
| A good encryption algorithm should be very much sensitive to the key. Sensitivity in key plays an important role because to some extent it eliminates the element of cryptanalysis. The Security strength of RSA and ABE are analysed and compared in the following graphs. |
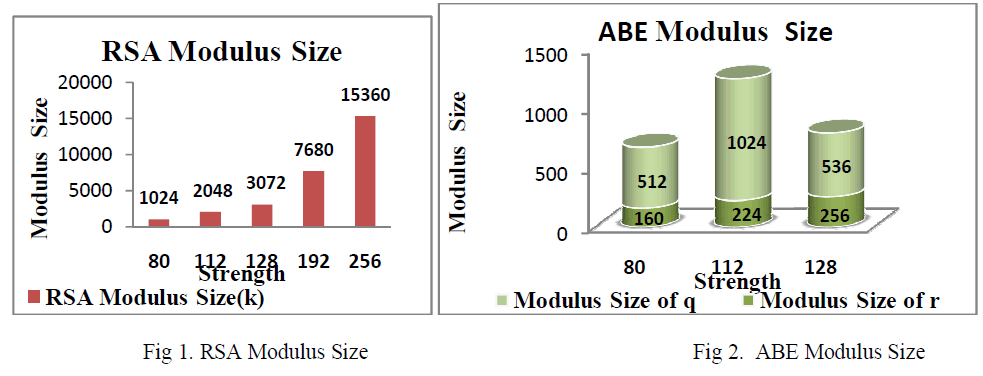 |
| RSA algorithm is applied in a wide field of information security, its security has withstood decades of challenges. But the security of key is different from the security of algorithm, which is often ignored by most of professionals. Here in Fig 1, the generation of keys according to the security levels (in bits) are shown for RSA. In most implementations, they lack legible recognition to the safety of the RSA key, so that even the introduction of some strong cryptoalgorithms still leads to some security matters. |
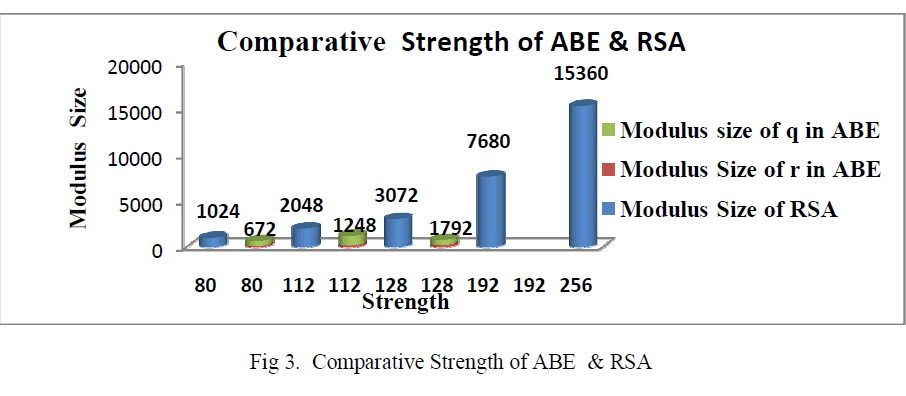 |
| As shown in the above Fig 2, the security strengths of Attribute based encryption(ABE) are measured with two parameters namely the modulus size of q and the modulus size of r. They are graphically represented with the security levels(in bits).For actual encryption/decryption of data RSA algorithm is used. It belongs to Advance encryption Standard i.e. AES. The RSA uses public & a private key. It is the one way function and uses large integers (e.g. 1024 bits).In the above Fig 3, the security strengths of RSA and the Attribute based encryption are compared with the generated modulus size. |
CONCLUSION |
| With the speedy expansion of cloud computing, data security and privacy protection become the critical problems in the research of cloud computing. The keys are generated based on the different cryptographic algorithms. This paper flings elucidation on data securing algorithms such as RSA and ABE. The security strengths of Attribute based encryption schema and RSA are compared and examined based on different cryptographic algorithms such as Pairing based Cryptographic algorithm and Integer Factorization Cryptography. |
References |
|