ISSN ONLINE(2320-9801) PRINT (2320-9798)
ISSN ONLINE(2320-9801) PRINT (2320-9798)
Karishma Talan1, G R Bamnote2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering
The shortest paths, sets of paths with the shortest distance between a single initial (source) point and all other destination points, as well as between all pairs of points, are to be found. For each of these approaches, individual algorithms with specific features have been worked out over the past decades. Graph-like data appears in many applications, such as social networks, internet hyperlinks, roadmaps, etc. and in most cases, graphs are dynamic, evolving through time
KEYWORDS |
| Shortest path problem; A * (Star) algorithm; Minimum weight node first Principle, efficiency evaluation |
I. INTRODUCTION |
| The shortest distance between two points is a straight line. But in the real world, if those two points are located at opposite ends of the country, or even in different neighbourhoods, it is unlikely to find a route that enables to travel from origin to destination via one straight road. Find out a map to determine the fastest way to drive somewhere, but these days, it is just as likely to use a Web-based service or a handheld device to help with driving directions. The popularity of mapping applications for mainstream consumer use once again has brought new challenges to the research problem known as the “shortest-path problem.”[1] |
| The shortest-path problem, one of the fundamental quandaries in computing and graph theory, is intuitive to understand and simple to describe. In mapping terms, it is the problem of finding the quickest way to get from one location to another. Expressed more formally, in a graph in which vertices are joined by edges and in which each edge has a value, or cost, it is the problem of finding the lowest-cost path between two vertices.[1] The shortest path problem can be defined for graphs whether undirected, directed, or mixed. It is defined here for undirected graphs; for directed graphs the definition of path requires that consecutive vertices be connected by an appropriate directed edge. |
| The problem is also sometimes called the single-pair shortest path problem, to distinguish it from the following variations: |
| • The single-source shortest path problem, to find shortest paths from a source vertex v to all other vertices in the graph. |
| • The single-destination shortest path problem, to find shortest paths from all vertices in the directed |
| • graph to a single destination vertex v. This can be reduced to the single-source shortest path problem by reversing the arcs in the directed graph. |
| • The all-pairs shortest path problem, to find shortest paths between every pair of vertices v, v' in the graph. |
| These generalizations have significantly more efficient algorithms than the simplistic approach of running a single-pair shortest path algorithm on all relevant pairs of vertices. |
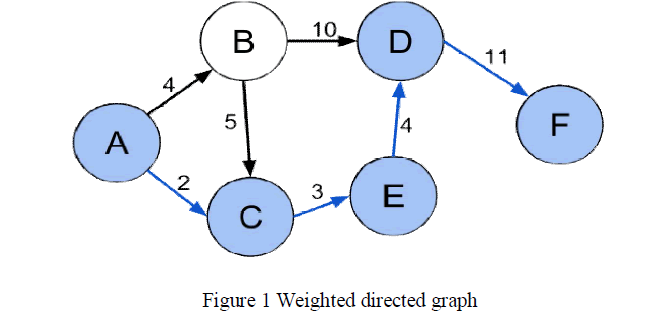 |
| [Shortest path (A, C, E, D, F) between vertices A and F in the weighted directed graph.] |
| A road network can be considered as a graph with positive weights. The nodes represent road junctions and each edge of the graph is associated with a road segment between two junctions. The weight of an edge may correspond to the length of the associated road segment, the time needed to traverse the segment or the cost of traversing the segment.[4] |
II. RELATED WORK |
| The classic general algorithm for shortest path is called Dijkstra's algorithm, first presented in 1959. But although this solves the problem, it does so essentially by searching the entire graph to compute its lowest-cost path. For small graphs, this is feasible, but for large graphs, the computing time just takes too long. For example, in a solution for driving directions, the road network is represented as a graph, where each vertex corresponds to an intersection and each edge to a segment of road between intersections. A complete map of the U.S. road system contains more than 20 million intersections, a huge amount of data to process if the algorithm has to search every segment of the graph. [8] |
| It would not have been realistic for a portable device to store a map of the United States; the user would have loaded data for a local map, and then reloaded a different map if traveling to a different area. But now, devices have the capacity to store a full map of North America or Europe,” says Renato Werneck, researcher at Microsoft Research Silicon Valley.[5] A heuristic solution required looking at a very large portion of the map. There were no performance guarantees, and the solutions were non-exact. The algorithms must be exact and efficient. Just 0.1 percent of the graph is visible and still find an exact shortest-path solution. This turned out well, because shortest path is a fundamental problem for which new solutions are found, and some of the work made it into production.[5][3] |
| Shortest-path implementations are commonly deployed in two stages. In the first stage, algorithms preprocess a data model of the road network to derive information that will help reduce the search time for queries. The second is the actual algorithm to solve user queries. In production environments, servers or portable devices are loaded with preprocessed data, reducing the amount of data that query algorithms need to search. Therefore, the speed of a solution depends on both the quantity of preprocessed data and the efficiency of the query algorithm. |
| Dijkstra's algorithm, conceived by computer scientist Edsger Dijkstra in 1956 and published in 1959, is a graph search algorithm that solves the single-source shortest path problem for a graph with non-negative edge path costs, producing a shortest path tree. This algorithm is often used in routing and as a subroutine in other graph algorithms.For a given source vertex (node) in the graph, the algorithm finds the path with lowest cost (i.e. the shortest path) between that vertex and every other vertex (although Dijkstra originally only considered the shortest path between a given pair of nodes). It can also be used for finding costs of shortest paths from a single vertex to a single destination vertex by stopping the algorithm once the shortest path to the destination vertex has been determined. For example, if the vertices of the graph represent cities and edge path costs represent driving distances between pairs of cities connected by a direct road, Dijkstra's algorithm can be used to find the shortest route between one city and all other cities. As a result,the shortest path algorithm is widely used in network routing protocols, most notably IS-IS and OSPF (Open Shortest Path First).[2][6] |
| Dijkstra's original algorithm does not use a min-priority queue and runs in time O(v2)(where is the number v of vertices). |
| Point-to-Point Shortest Path Algorithms with Preprocessing |
| The classical point-to-point shortest path problem (P2P): given a directed graph G = (V, A) with non-negative arc lengths and two vertices, the source s and the destination t, find a shortest path from s to t. More interesting is to find exact shortest paths. Preprocessing is allowed, but limit the size of the precomputed data to a constant times the input graph size. Preprocessing time is limited by practical considerations. For example, for computing driving directions on large road networks, quadratic-time preprocessing is impractical. |
| Note that preprocessing-based algorithms have two parts: preprocessing algorithmand query algorithm. The former may take longer and run on a bigger machine or a cluster of machines. The latter need to be fast and may run on a small device.For the P2P case, note that when the algorithm is about to scan the destination t, d(t) is exact and the s-t path defined by the parent pointers is a shortest path. One can terminate the algorithm at this point. This termination rule gives Dijkstra’s algorithm for the P2P problem. This algorithm searches a ball with s in the center and t on the boundary.[10] |
| The shortest path problem is a fundamental problem with numerous applications. This is one of the most common variants of the problem, where the goal is to find a point-to-point shortest path in a weighted, directed graph. This problem is referred to as the P2P problem. It is assume that for the same underlying network, the problem will be solved repeatedly. Thus, preprocessing is allowed with the only restriction that the additional space used to store precomputed data is limited: linear in the graph size with a small constant factor. The goal is a fast algorithm for answering point-to-point shortest path queries. A natural application of the P2P problem is providing driving directions, for example services like Mapquest, Yahoo! Maps and Microsoft MapPoint, and some GPS devices. One can spend time preprocessing maps for these applications, but the underlying graphs are very large, so memory usage much exceeding the graph size is prohibitive. |
Labeling Method and Dijkstra's Algorithm |
| The labeling method for the shortest path problem finds shortest paths from the source to all vertices in the graph. The method works as follows. For every vertex v it maintains a distance label d(v), a parent p(v), and a status S(v) ∈ {unreached, labeled, scanned}. Initially d(v) = ∞, p(v) = nil, and S(v) = unreached for every vertex v. The method starts by setting d(s) = 0 and S(s) = labeled. While there are labeled vertices, the method picks a labeled vertex v, scans all arcs out of v, and sets S(v) = scanned. To scan an arc (v, w), one checks if d(w) > d(v) + âÃâÃâ(v, w) and, if true, setsd(w) = d(v) + âÃâÃâ(v, w), p(w) = v, and S(w) = labeled. If the length function is non-negative, the graph has no negative cycles and the labeling method terminates with correct shortest path distances and a shortest path tree defined by the parent pointers. Its efficiency depends on the rule to choose a labeled vertex to scan next. Define d(v) to be exact if it is equal to the distance from s to v. If one always selects a vertex v such that, at the selection time, d(v) is exact, then each vertex is scanned at most once. Dijkstra [5] and independently Dantzig observed that if âÃâÃâ is non-negative and v is a labeled vertex with the smallest distance label, then d(v) is exact. The labeling method with the minimum label selection rule is known as Dijkstra’s algorithm. If âÃâÃâ is non-negative then Dijkstra’s algorithm scans vertices in nondecreasing order of distance from s and scans each vertex at most once |
III. PROPOSED ALGORITHM |
A star Algorithm with Minimum Weight Node FirstPrinciple |
| A* is the graph search and traversal algorithm that makes use of some additional function that decreases when we are approaching the goal node in the graph. The helper function (called heuristic function) needs not be precise but it must not overestimate the distance till the goal. If the graph exists in real world space (roads, railways, computer networks, etc), the good value for this function is the spatial ("euclidean") distance till the goal node. Heuristic function must be known for every node in the graph (it is zero for the goal node). Dijkstra algorithm is a separate case of A* algorithm where heuristic function is always zero (0).[8][9] |
| Same as Dijkstra algorithm, the algorithm assigns the "distance value" to every node. This value is the distance (cost) to reach the node from the initial (starting) node. This value is of course zero for the initial node itself. At the start of the algorithm, it is set to be infinite for all other nodes in the graph. The algorithm also needs to remember the collection of already visited nodes. The "current node" is initially set to the initial node.[12] |
| Minimum Weight Node FirstPrinciplestates to optimize the doubly-linked queue, that is, finding the vertex with the minimum distance to the source node and pop the vertex to the front of the queue.[3] |
IV. PSEUDO CODE |
| 1. Create the open list of nodes, initiallycontaining only our starting node. |
| 2. Create the closed list of nodes, initially empty |
| 3. while (we have not reached our goal) |
| { |
| Consider the best node in the open list (node with the lowest f value) |
| if (this node id the goal) |
| { |
| then we are done |
| } |
| else { |
| move the current node to the closed list and consider all of its neighbors |
| For (each currently explored neighbor node) |
| if (this neighbor is in the closed list and our current g value is lower |
| { |
| update the neighbor with the new, lower g value |
| Change the neighbor’s parent to our current node |
| } |
| else if (this neighbor is in the open list and our current g value is lower ) |
| { |
| update the neighbor with the new, lower g value |
| Change the neighbor’s parent to our current node |
| } |
| else |
| this neighbor is not in either the open or close list { |
| add the neighbor to the open list and set its g value |
| } |
| } |
| } |
| } |
V. CONCLUSION AND FUTURE WORK |
| With the A Star search algorithm it is possible to find the shortest path from one point to another on a map (while respecting fields that may not be walkable or that may slow down the movement). If our goal is not to find the path to one concrete point but to find the closed point that fulfills some condition, you should use Dijkstra’s algorithm instead. The worst-case running time for the Dijkstra algorithm on a graph with nodes and edges is because it allows for directed cycles. It even finds the shortest paths from a source node to all other nodes in the graph. This is basically for node selection and for distance updates. While is the best possible complexity for dense graphs, the complexity can be improved significantly for sparse graphs. |
| While A* is generally considered to be the best path finding algorithm (see rant above), there is at least one other algorithm that has its uses - Dijkstra's algorithm. Dijkstra's is essentially the same as A*, except there is no heuristic (H is always 0). Because it has no heuristic, it searches by expanding out equally in every direction. As you might imagine, because of this Dijkstra's usually ends up exploring a much larger area before the target is found. This generally makes it slower than A*. |
| Introduction to an effective Minimum Weight Node First Principle -based A star algorithm for shortest path distance computation in large graphs. It is planned to achieve more efficiency than dijkstra algorithm. As A Star algorithm is extension of dijkstra algorithm and with Minimum Weight Node First Principle it will give more efficiency and performance will be improved. |
References |
|