ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
K.P.R.Rao1 , D.Vasu Babu2 , E.Taraka Ramudu3
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
In this paper, we introduced parametric s-metric space and proved two unique common fixed point theorems in it. Our result generalizes and improves two main results of Ionescu,Rezapour and Samei [4].
Keywords |
| Parametric s-metric space, compatible maps, Weakly compatible maps. |
| 2000 Mathematics Subject Classifications : 47H10, 54H25. |
I. INTRODUCTION |
| The concept of fuzzy sets was intiated by Zadeh [10] in 1965 . The fuzzy metric space was introduced by Kramosil and Michalek [8]. Also, Grabeic[11] proved the contraction principle in the setting of fuzzymetric space. Also, George and Veeramani [1] modified the notion of fuzzy metric space with the help of continuous t-norm, by generalizing the concept of probablistic metric space to fuzzy situation. Later several authors, for example Vasuki [13],Pant[15] , Mishra et al.[14] ,Bari et al.[3], Vetro et al. [5] etc. proved fixed and common fixed point theorems in fuzzy metric spaces. We now state the following |
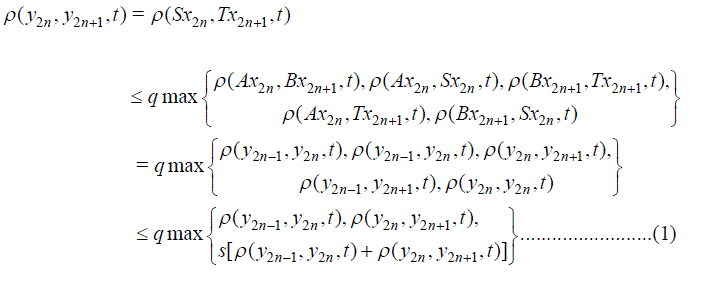 |
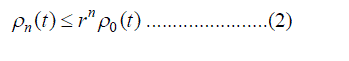 |
| Then (M, N) is called an intuitionistic fuzzy metric on X . The functions M(x, y,t) and N(x, y,t) denote the degree of nearness and the degree of non-earness between x and y with respect to t , respectively. |
| Definition 1.6[4]: Let (X,M,N,*,ïÃÆà) be an intuitionstic fuzzy metric space. The fuzzy metric (M, N) is called triangular whenever, |
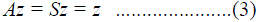 |
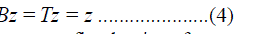 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
References |
|