1Departamento de Matematica, Facultad de Matematica, Astronoma y Fsica (FAMAF),Universidad Nacional de Cordoba, Argentina
2Departamento de Fsica, Instituto de Fsica Aplicada (INFAP), Universidad Nacional de San Luis, Argentina
Received date: 18/11/2015 Accepted date: 27/01/2016 Published date: 31/01/2016
Visit for more related articles at Research & Reviews: Journal of Statistics and Mathematical Sciences
An extension of previous results is obtained concerning the evolution equations that satisfy not only the dynamical variables but the space-time correlations which constitute a hierarchy of differential equations. The stochastic evolution equations are Non-Markovian, and the corresponding Markovian evolution equations are obtained as a particular case when the evolution depends on the nearest previous time step. A relatively simple illustrative example is given allowing to obtain some previous results as limiting cases.
Non-Markovian stochastic evolution equations, Correlation, Space-time correlations.
An extension of previous results [1-7] will be obtained in the present paper. The present approach, which could be coined discrete stochastic updating equations (DSUE) and is different from the usual stochastic calculus like the one developed by Ito and Stratonovich or Kurtz [8], provide a tool that allow to obtain a hierarchy of differential equation for interpolating functions whose solution give the evolution not only of the dynamical variables but also of the correlations. The stochastic Non-Markovian discrete evolution equations for both the dynamical variables and space-time correlations are obtained and after an average over an ensemble of realizations a set of deterministic discrete evolution equations are obtained. A smooth interpolating function is introduced and the solution of the set of (in general) coupled differential equation that it satisfy, provides an increasing accuracy, depending of the order of the expansion in a Taylor series, of both, the dynamical variables and correlations.
The paper is organized as follows. In section II, the update of a set of discrete stochastic evolution equations, is defined and the necessary steps to obtain a set of interpolating functions are given. In Section III, a relatively simple illustrative example is given in order to provide some previous results as limiting cases. Finally, in section IV, the general features of the approach and conclusions are sketched.
In ref. [7] the basic definitions for a non-Markovian discrete stochastic evolution updating were given and reproduced below, with the appropriate modifications, for the sake of completeness and in order to provide the basic definitions used in the next sections. In order to make the presentation as simple as possible, and due to the results of the theorem proved in ref. [7], a one- dimensional lattice Λ with periodic boundary conditions in an interval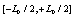 
( 
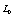being as large as we please but finite) will be considered and a set of complex dynamical variables 
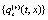will be used for describing the value of each dynamical variable in a realization r , in a state or type of dynamical variable s , at spatial coordinate 
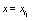and at time 
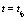. The spatial coordinate and time correspond to the discrete generic site 
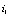and discrete update 
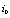, respectively. s designate the generic value of the set 
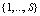, where S is the number of elements of the set. The spacings between sites is a1 and successive time is a0 . The number of lattice sites is 
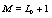and the length of the lattice is 
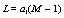The evolution equation for the set of dynamical variable can be expressed, as in ref. [7], in the following general form
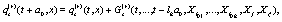
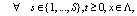
where G denote the set of updating rules that define a given model and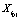 
....
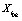denote the set of complex dynamical variables 
...,
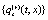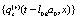respectively. The set of both discrete and continuous stochastic variables that confer stochasticity to the evolution equations are 
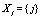and 
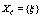, respectively. The sets of stochastic variables depends on the particular realization r and previous time 
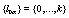The number of previous time is k +1 and the set is 
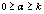any 0 ≥α ≥ k . The stochastic variables are chosen from sets of values according to given distributions. Usually, in the illustrative examples and for the sake of simplicity in the presentation, the stochastic variables are chosen at random and according to uniform distributions in such a way that all of them are statistically independent and a factorization of each product that contain stochastic variables is then possible. Let us consider a stochastic evolution equation (which is a special case of Eq.(1) and will be used in the illustrative examples) of the form
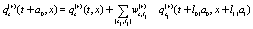
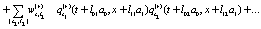
(2)
in order to derive non-Markovian stochastic equations of the Langevin-type or, after an average over realizations, deterministic evolution equations. It was used the short hand notation l2-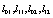
to save printing. Likewise S1 = s1 and s2 = s1, s2. The number of equations is 
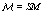. The stochastic weights and the dynamical variables, in Eq.(2), are labeled with an index r emphasizing that the value depends on a specific realization. The stochastic weights can, in general, be a complex number with a real 
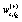and an imaginary part 
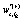, for any k , with 
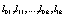. All generalized functions can be approximated or smoothed using some continuous function that provides the values of the generalized functions as "accurate" as possible [6]. Beside the evolution equations for the dynamical variables it is possible to construct other evolutions equations that are functions of the above mentioned dynamical variables, among others the evolution equations for the correlations consisting in products of dynamical variables which constitute a hierarchy of evolution equations. For example the product of two dynamical variables can be constructed as
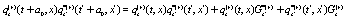
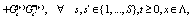
where it was used the short hand notation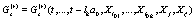 
, 
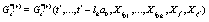, etc. The starred magnitudes are the complex conjugated of the corresponding complex number and 
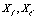are sets of stochastic variables, in general different, of 
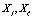. Also (t, x) and 
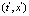designate two different space-time points. In order to obtain the corresponding deterministic evolution equations it must be averaged over an ensemble of realizations the set of stochastic evolution equations. The final result is
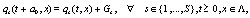(4)
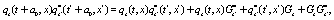
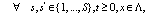(5)
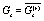
where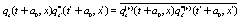 
, 
, 
, 
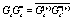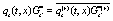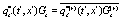, etc.
The overbar denotes an average over an ensemble of realizations. Note that even when it was used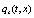 
, for the sake ofsimplicity in the notation, up to Eqs.(4,5) it must be understood as discrete dynamical variables with subscripts 
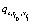which designate the discrete nature of the evolution equations (see at the beginning of this section where it was defined 
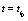and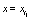 
It is not difficult to see that, the evolution equation obtained after the replacement of 
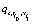by , becomes now a smooth function with 
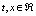, that also satisfy the discrete evolution equations for all the discrete values tio and xi1 . This is precisely the usual characteristic of an interpolating function. Of all possible interpolating functions that satisfy Eq.(4,5), this is the one that was chosen for the sake of simplicity and will be used here.
In order to obtain the partial differential equation for the evolution of the interpolating functions it is necessary to let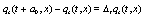 
, 
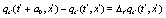and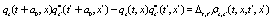 
, where 
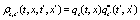, obtaining the following equations.
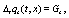
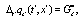(6)
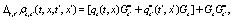(7)
that will be used in the examples developed in the next sections. The final step, needed for find partial differential equations allowing to provide an increasingly accurate value to the exact interpolating functions, is to expand both two sides of Eqs.(6.7) in a Taylor series up to a given order. It must be emphasized that Eqs.(6.7) are two evolution equations that allows to determine smooth interpolating functions corresponding to the set of discrete evolution equations given in Eqs.(4,5), respectively. As is easily seen, once the averages over an ensemble of realizations is performed, the corresponding equations are deterministic and consequently ordinary calculus must be used. The solution to the set of partial differential equations allows to determine the interpolating functions and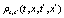 
as accurate as we please, by simply increasing the order of the expansion. This is the difference with the usual Ito and Stratonovich calculus which is based on Riemann-Stieltjes integrals or the usual stochastic evolution equations obtained using Kurtz theorem [8].
The simplest Non-Markovian stochastic evolution is
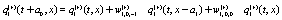
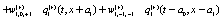
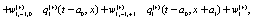
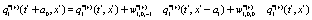
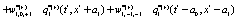
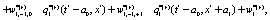(8)
Where the values of the dynamical variables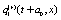 
and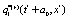 
depends linearly on the dynamical variables at two previous time step and also on additive noises 
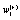and 
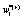, respectively. After averaging over an ensemble of realization, assuming that all stochastic variables 
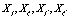are statistically independent, performing an expansion in a Taylor series up 
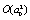and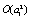 
, and after collecting terms, the following differential equations are obtained
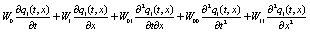
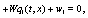
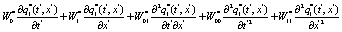
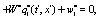(9)
Where
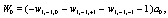
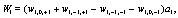
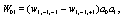
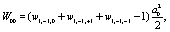
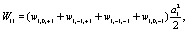
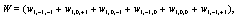(10)
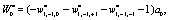
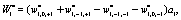
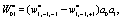
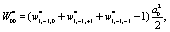
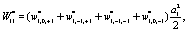
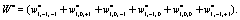(11)
The correlation, obtained after making the product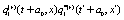 
and averaging over an ensemble of realization, is
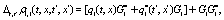
where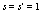 
and
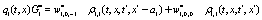
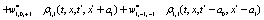
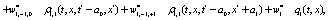
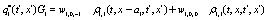
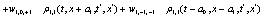
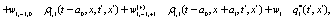
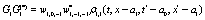
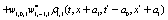
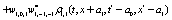
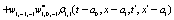
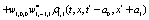
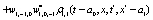
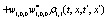
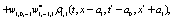
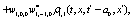
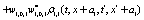
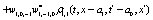
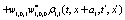
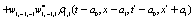
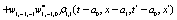
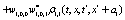
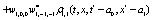
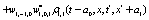
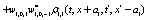
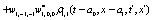
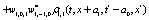
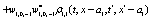
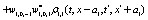
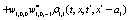
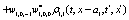
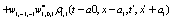
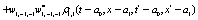
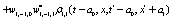
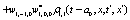
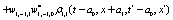
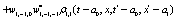
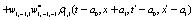
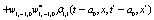
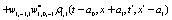
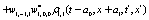
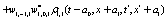
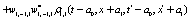
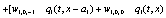
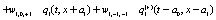
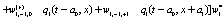
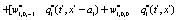
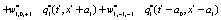
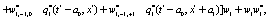
Where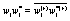 
Moreover, if 
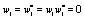the last six lines in the right hand side in Eq.(15) and the last term in Eqs.(13,14) become zero and the evolution equation for the correlation is not coupled to the evolution equation for the dynamical variable. Note that it was assumed that all stochastic variables are statistically independent and the factorization was possible. After inserting Eqs.(13-15) in Eq.(12) and expanding in a Taylor series up to 
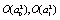the evolution equation for the interpolating function for the correlation, can be obtained. Using the shorthand notation 
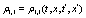, the final result is
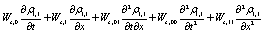
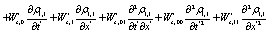
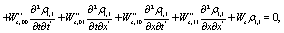(14)
where the coefficients can be expressed as a function of the w s, and are long expressions which it will be not given explicitly in order to save print and also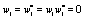 
was assumed for the sake of simplicity. Of course, even when this expressions at first glance seems to be too much cumbersome to obtain, the use of a symbolic manipulator like MAPLE [9], make the task very simple and efficient.
If t = t′ it is possible to recover the Non-Markovian space correlations.
If x = x′ it is possible to recover the Non-Markovian time correlations.
In order to recover the Markovian evolution equation it is necessary to let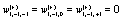 
and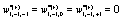 
in Eq (8). If in addition t = t′ the evolution equation corresponding to the first illustrative example in ref. [7] is recovered after using the appropriate weights and orders of the Taylor series expansion.
An extension of the results given in ref. [7] was obtained in the present paper. The space correlation was extended in order to obtain a space-time correlation allowing to derive previous results as special cases. Three illustrative limiting cases were given at the end of section III. Also the differences with other usual approaches (e.g. Ito and Stratonovich calculus or Kurtz theorem) was given at the end of section II, in order to clarify some previous controversies or misunderstandings with the present approach. Other extension to Non-Markovian evolution equations depending on more than two previous time step are also easily obtained (for the case of three previous time step see subsection 3.2 of ref. [6]).
The authors want to thank V. D. Pereyra for reading the manuscript.
Menu