Department of Physics, National Chung-Hsing University, 250 Guo-Kuang Road, 402 Taichung, Taiwan
Received date: 18/01/2016 Accepted date: 30/01/2016 Published date: 02/02/2016
Visit for more related articles at Research & Reviews: Journal of Statistics and Mathematical Sciences
Stock markets, Stock index, Crossover-fractal structure.
In 1900, Bachelier [1] was the first to consider the variation of stock prices as a path of random walk. Subsequent researchers found, however, the ups and downs of the stock indices are different from randomness except for very long time scales. Clear evidence of this non-randomness is that the distribution of returns is not Gaussian but universally has a fat tail [2]. Optimistic researchers quickly attempted to utilize the information gathered from these returns to predict the market [3,4]. Others have used agent-based models to generate series with return distributions similar to the real ones [5]. Here we have shown that the time sequences of some stock indices behave like the trajectory of a weakly-persistent random walk (WPRW). The trajectory of a WPRW is a crossover-fractal [6], a fractal which has one fractal dimension for short scales and another for large scales. We studied various pieces of stock index series from ten different countries and found that some of them were crossover-fractals with the crossovers at about 20 minutes. Beyond that time the fractal dimension was close to 1.5, much like a simple random walk. Since the longrange variance of the WPRW is larger than that of a random walk, the stock index is harder to predict than a random walk. On the other hand, because of this persistent feature, one can exploit the market at shorter scales than 20 minutes and always profit by high-frequency transactions.
The stock market is affected by many external factors, such as earthquakes, political elections and the invention of new techniques. In general, external factors affect the values of returns at certain times and can last for days. These factors build the trends of the market. Previous studies have focused on the distribution of returns and have found the shape of the distribution is different than normal distribution and roughly universal for stock indexes everywhere in the world [7-14]. Contrary to the distribution of returns, which is mainly a result of external effects, the fluctuation of the markets shown in the local ups and downs of the stock index at a minute scale is due to the battle for profits between agents. This battle is intrinsic to the system and little affected by external effects. To illustrate this point, we digitized the real stock index S and P500 by replacing the non-zero values of returns with a constant while retaining their signs. This produced an artificial series (Figure 1). The collapse of the US market in October 1987 that was conspicuous in the real series did not stand out in the digitized surrogate. That is, neglecting the differences in the values of returns, the stock index apparently behaves similarly all the time. In further characterizing the intrinsic properties of non-stationary time sequences such as stock indexes, we have found fractal dimension to be a useful parameter.
Figure 1: S and P500 index in 1987 and its digitized surrogate wherein non-vanishing returns are replaced by ̱̉ 1.
When Mandelbrot introduced the concept of fractals, his intention was to uncover the fractal properties of the price variation of goods [15]. People soon realized the monofractal was not enough for describing real data and introduced the concept of multifractals, which used more than one parameter to characterize the same sequence of data [16-18]. However, the application of multifractals to real market data has not so far produced much success. A different extension of the fractal concept is the scale-dependent fractals [19,20], which might be better candidates for characterizing real time sequences in practice. For a time sequence, the variation of the data over an intervals (scale) is in general dependent on the value of s. Special sequences such as the trajectory of a random walk and a Weierstrass function, which each have a single fractal dimension for any value of s, are called monofractals. For the last 15 years people have used the DFA method [21] to detect fractal properties of various time sequences at different scales. Interestingly, a significant number of elements including heart rate signals [22,23], fluctuations of fatigue crack growth [24], wind speed data [25], precipitation and river runoff records [26] and stock indexes [27] behave like crossoverfractals. That is, these time sequences have a fractal dimension for scales smaller than a certain value and a second fractal dimension for scales larger than the value. Here we used the mIRMD method [6,28] to calculate the scale-dependent dimension of stock indexes at one-minute intervals.
We calculated the average midpoint displacements <G(s)> of all scales s for a time series f(x):
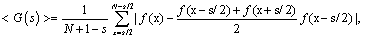, (1)
Where N is the number of data points. For fractals of dimensions between 1 and 2, (<G(s)>) is proportional to s2-D, so that the fractal dimension is given by 2 subtracted from the slope of the linear fit for the plot of log (<G(s)>) versus log(s) [6,28]. We found that various pieces of indexes at one-minute intervals of the S and P500 during the period between 1986 and 1992 were all crossover-fractals (Figure 2a). They had a fractal dimension of about 1 for shorter time scales than 20 minutes and close to 1.5, similar to a random walk, for larger scales. We also found that the crossover-fractal properties of these time series were well preserved in their digitized counterparts. We then calculated the fractal dimensions of the stock indexes records of nine other markets around the world from September 2008 to June 2009 [29]. The results (Figure 2b) showed that two markets (China_ SSEC, Taiwan_TAIEX), similar to the US_S and P500, were crossover-fractals. Another three (France_CAC40, Germany_XDAX and Portugal_PSI20) were more like monofractals while others (Australia_AORD, Brasil_BVSP, India_SENSEX, Japan_NIKKEI225) were somewhere in between in that they showed slightly crossover-fractal structures.
Figure 2: Fractal dimensions of stock indexes calculated by the mlRMD method: (a) S and P500 (7 years average) (b) 9 other markets around the world (10 months average).
Note that the crossover-fractals of the stock time series have smaller fractal dimensions in shorter time scales. Dynamically, the formation of this type of time series would be a process where a fractal of lower dimension in shorter scales gradually builds up a fractal of higher dimensions in larger scales. A simple model can effectively simulate this dynamic process. In markets, chasing a bull and avoiding the bear is always the choice for many agents. Within minutes, immediate access to past records of ups and downs of the index might be crucial to an agent’s decision to buy or sell. Based on this assumption, we constructed a simple model called the weakly-persistent random walk (WPRW) model. The model works as follows:
1. Following two consecutive ups (downs), there is a probability, 5.0>p, the index will be up (down) at the third minute.
2. Following an up (down) then a down (up), the probability of being up (down) at the third minute is5.0≈q.
In other words, in the WPRW the index sequence is more likely to be persistent in the same direction of the last two minutes. When it goes in different directions for the last two minutes, the direction it will go at the third minute is unknown. A typical trajectory generated by the WPRW is very much like a digitized version of a real stock sequence as shown in Figure 1. Fractal spectra calculated by mIRMD for some different values of p have been plotted in Figure 3. We saw that the WPRW trajectories behaved as crossover-fractals similar to real stock indexes. Indeed, we found the probability, p, of real index sequences considered in Figure 2 to be larger than 0.6 for those with crossover-fractal structure and close to 0.5 for those with a monofractal structure. This is consistent with the WPRW model.
Figure 3: Fractal dimensions of the trajectories generated from WPRW model: p=0.5, 0.6, 0.7, 0.8 and 0.9.
In the WPRW we assumed the stock index would always go either up or down at any minute. However, the real stock index does remain unchanged for a certain percentage of time (8% for S and P500 in 1987) at the one-minute scale. We have considered some modified models of the WPRW by accommodating the probability of indexes remaining stationary. The crossoverfractal properties of the time sequences generated by these modified models were qualitatively the same as those of the WPRW. The position of crossover can also be adjusted slightly by using different versions of the model.
A corollary of the WPRW model is that stock markets with crossover-fractal structures are more unpredictable than random walks in the long scale. Because its symmetric persistence (with a probability p>0.5) is in both up and down directions, the possible values of the index after a period of time spread over a wider range than a random walk The random choice (with probability q=0.5) in up-down and down-up cases makes the distribution of the possible values close to a Gaussian one in the long scales, a corollary of the central limit theorem. Therefore, for a scale longer than 20 minutes (for p less than 0.85), the index sequence behaves like a random walk but diffuses faster than a normal one.
On the other hand, because of its crossover-fractal properties, the stock index behaves differently than a random walk in time scales of less than 20 minutes. Unlike a random walk, which cannot be predicted at each step (minute), the WPRW demonstrates a preference of direction when the last two steps are in the same direction. This weakly-persistent property, while making the stock index harder to predict than a random walk in the long scale, gives the traders a chance to bet on the right direction at times in minute scales. Let us assume that the index represents the price of a stock. If a trader buys the stock when its price goes up in the last two minutes and does not sell it until its price goes down in two consecutive minutes, he is likely to profit in the long run (if transaction costs are ignored). The trader would do this by alternating the buying and selling transactions whenever two consecutive ups and downs respectively appeared.
As a demonstration, we applied the WPRW rule to the time series of the S and P500 index of 1987. The net gain at selling was always positive and increased with time. The average time interval between transactions in this case was about 10 minutes. It increased to 32 minutes when we used an even weaker form of persistent rule, buying and selling the stock whenever four consecutive ups and downs occurred, respectively. When transaction costs were taken into consideration, we found that the net gain at the end of the index series was still positive if transaction costs were less than 0.05% of the selling price. We obtained similar results for other stock indexes (China_SSEC and Taiwan_TAIEX) that had a crossover-fractal structure.
We have shown that the time series of the weighted average index of some stock markets are crossover-fractals and can be exploited by traders using the WPRW rules. The immediate question is whether the strategy of WPRW works for a single stock. In general, the answer is “no.” The time sequence of the price of a single stock has a different fractal property than the average index. The weakly-persistent property appears only in the average index of the combination of a sufficient number of stocks. That is, one has to build a portfolio to include an appropriate combination of stocks before he can exploit its weakly-persistent feature.
This work is supported by grants from the National Science Council under the grant number NSC97-2112-M005-001, and the National Centre for Theoretical Sciences of Taiwan.
Menu