ISSN ONLINE(2320-9801) PRINT (2320-9798)
ISSN ONLINE(2320-9801) PRINT (2320-9798)
| M. Eniya1, M. Vinothkumar M.E.,(Ph.D) 2 |
| Corresponding Author: SHARMA VIVEK, E-mail: vivek03sharma@rediffmail.com |
| Received: 23 September 2014 Accepted: 11 February 2015 Published: 21 March 2015 |
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering
A multi-agent system (MAS) is an automated system which consists of multiple agents. MAS can be used to solve the problems that are difficult to solve by human. Agents are connected with each other; they have access to other agent via connection. The problems and functions are not stored automatically in agent, agents uses their connections for storage. High storage in connections may leads to occur memory insufficient. This memory insufficient also creates the changeability of apparent input. This memory insufficient has allowed us to define the model of MAS by using markov property. Here we use markov chain model to define strength of MAS. The number of states varies according to the capability of original agents. We then explore the strength of evolving agent growth through simulation and compare the results with non-derive MAS. We can implement classified agents in data extraction from cloud data server.
Keywords |
| Clusters, Distortion, k-Nearest Neighbor, Multi-Agent System, Stability |
INTRODUCTION |
| The main application areas of data mining are in Business analytics, Bioinformatics, Web data analysis, text analysis, collective science problems, biometric data analysis and many other provinces where there is scope for hidden information retrieval. Some of the challenges in front of the data mining researchers are the handling of complex and capacious data; disseminate data mining, organizing high dimensional data and model optimization problems. In the coming sections the various stages occurring in a typical data mining problem are described. The different data mining models that are commonly applied to various problem domains are also discussed in detail in the coming sections. Data mining strategies can be grouped as follows: |
| A. Classification - Here the given data instance has to be classified into one of the target classes which are already known or defined. One of the examples can be whether a customer has to be classified as a trustworthy customer or a defaulter in a credit card transaction data base, given his various demographic and previous purchase characteristics. |
| B. Estimation - Like categorization, the suggestion of an evaluation model is to determine a value for an unknown output element. After all, unlike categorization, the output elements for an evaluation difficulty are numeric rather than categorical. |
| C. Prediction- It is not easy to differentiate prediction from categorization or evaluation. The only variation is that rather than determining the current behavior, the predictive model predicts a future outcome. The output attribute can be categorical or numeric. An example can be “Predict next week’s closing price for the Dow Jones commercial median”. Explains the assembly of a decision tree and its predictive applications. |
| D. Association rule mining - Here interesting hidden rules called association rules in a large transactional data base is mined out. |
| E. Clustering - Clustering is a special type of classification in which the target ratings are concealed. For example given 100 customers they have to be classified based on certain similarity criteria and it is not preconceived which are those classes to which the customers should finally be grouped into. |
| Any data mining work may involve various stages. Business understanding involves understanding the domain for which the data mining has to be performed. The various domains can be financial domain, educational data domain and so on. Once the domain is understood properly, the domain data has to be understood next here relevant data in the needed format will be collected and understood. Data preparation or pre-processing is an important step in which the data is made suitable for processing. This involves cleaning data, data modification, collecting subsets of records etc. When data is prepared there are two phases, namely collection and modification. Data selection means selecting data which are useful for the data mining purpose |
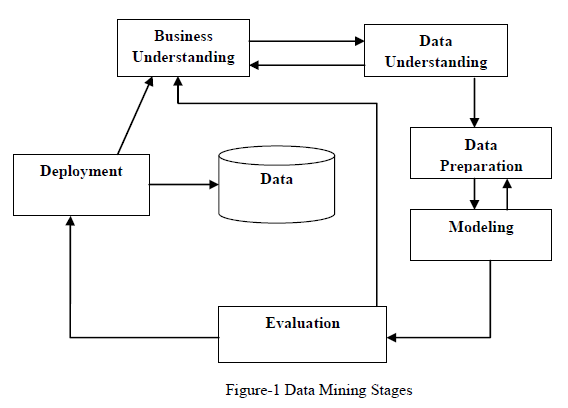 |
| It is done by selecting required attributes from the database by performing a query. Data transformation or data expression is the process of converting the raw data into required format which is acceptable by data mining system. For e.g., Symbolic data types are converted into numerical form or categorical form. Data modeling involves building the models like decision tree, neural network etc from above pre-processed data. |
II. BRIEF EXPLAINATION FOR EARLIEST TECHNIQUES |
| A.Formation Stability |
| Formation stability is a formation control framework for multiple agents with intermittent information exchange between the agents. In the case where the number of communication channels that can be used at each time instant is limited. Formation stability provide stability based on two condition, one is agent wise limited information. In an environment only one channel allowed for each agent at every instant and it does not allowed per agent. Second one is system wise limited information used to allowed only a limited number of channels which are not sufficient to produce a connected network topology |
| B.Time-dependent communication links |
| The weak assumption on the communication topology, we allow for nonbidirectional and time dependent transmission ornament. Oneway transmission is essential in practical applications and can easily be incorporated, for example, via broadcasting. Agents are processed based on some instant of time, the current processing agent update their state based on the information received from neighbouring agents according to a simple condition. Gathering information is not a trusted one. This means we allow for time dependent communication patterns which are important if we want to take into account link failure and link creation, reconfigurable networks and nearest neighbour coupling. |
| C.Discrete Time with Time-Varying delay |
| Time-Varying delay provide a class of consensus protocols, which are built on repeatedly using the same state information at two time steps. We establish that consensus problems are solvable under the same topology conditions as the typical ones and without the requirement that agents always ret their own instantaneous state information. Agents are sepearted to “points in time”, that is agents are move from one to next state at the same time the time period ia also moved to next state. The number of agents are finite and countable; in this the next state depends only on the current processing state. The current state losses its communication lines, the next state can not able to process further. |
III. OUR CONTRIBUTION IN PROPOSED SYSTEM |
| The study proposes an agent based computing based data mining platform to share different levels of clinical data and to extract knowledge from a huge number of raw data in various locations. Typically, the platform can be appealed to different hospitals, organizations as well as companies. More primarily, to our understanding, there are not many existing models that have been specifically focused on health informatics studies. Given the research discussion, not only does the study propose a robust information system to contribute the health data sharing in each region, but also the study has potential to promote international health informatics research collaboration. |
| The objectives of the study are: |
| ïÃâ÷ Survey the problem associated with embarce agent based computing in all kinds of research |
| ïÃâ÷ Explore solutions to conquer the barriers of implementing agent based computing for health data sharing among different geographic jurisdictions. |
| ïÃâ÷ Design a proof-of-concept agent based computing architecture for geographically distributed health data mining research. |
| In our proposed agent based Greedy K-Nearest neighbor clustering, we are given a set of N points in ddimension space Rd and we have to arrange them into a number of groups (called clusters). In k-nearest neighbor clustering group, the groups are identified by a set of points that are called the cluster group centers. The data position belongs to the cluster group whose center is closest. Existing algorithms for k-nearest neighbor clustering suffer from two main disadvantage, (i) The algorithms are moderate and do not scale to huge number of data points and (ii) they converge to different local minima based on the initializations. We present a fast greedy k-nearest neighbor algorithm that attacks both these downside based on a greedy k-NN algorithm. The approach is fast, deterministic and is an approximation of a global strategy to obtain the clusters. There are many popular models that can be effectively used in different data extract problems. Decision trees, Naive Bayes classifier, and Inactive learners, it carries vector machines, and backsliding based classifiers are some amid them. Conditional type of approach, nature of data and element, it can resolve which can be the most perfect model. Still there is no clear cut answer to the question of which is the best data excavate model. It can only say for a specific application one model is better than the other. |
| A.Decision trees |
| The decision tree is a popular categorization method. It is a tree like structure where each internal node denotes a decision on an element value. Each division constitute an outcome of the decision and the tree leaves constitute the classes. Decision tree is a representation that is both anticipating and expressive. A decision tree shows the correlation establish in the data attribute. |
| B.K-Nearest Neighbors Algorithm (k-NN) |
| The k-NN is a non- parametric method for classification and regression that predicts objects' "values" or class memberships based on the k closest preparation examples in the attribute space. k-NN is a type of illustration based learning, or inactive learning where the task is only approximated locally and all computation is deferred until categorization. The k-NN algorithm is the simplest of all machine learning algorithms; an object is classified by a majority vote of its adjacent, with the object being allocated to the class most common amongst its k nearest adjacent (k is a positive integer, typically small).Then the object is easily allocated to the class of that single nearest adjacent. The same method can be used for backsliding, by simply assigning the property value for the object to be the average of the values of its k nearby adjacent. It can be useful to load the benefactions of the adjacent, so that the nearer adjacent present more to the average than the more separation ones. The adjacent are taken from a set of entities for which the correct categorization is recognized. This can be impression of as the preparation set for the algorithm; however no clear preparation is required. The k-nearest neighbor algorithm is diplomatic to the local structure of the data. |
| C.Parameter selection |
| The best choice of k depends upon the data point; normally, vast values of k reduce the effect of noise on the categorization, but make deadline between classes less definite. A good k value can be selected by various searching techniques. The special case where the class is predicted to be the class of the closest training sample is called the nearest neighbor algorithm. The precision of the k-NN algorithm can be severely degraded by the presence of noisy or unrelated attributes, or if the feature scales are not orderly with their significance. The research effort is mainly selecting or scaling features to improve categorizations. Particularly parameter selection is the use of evolutionary algorithms to optimize feature scaling. |
IV.ALGORITHMS USED IN MAS |
| A.Greedy K-Nearest Neighbor on Agent Based |
| The fast greedy k-nearest neighbor algorithm uses the concepts of the greedy global k-nearest neighbor algorithm for overall solution. The halfway convergence is over using the restricted k-nearest neighbor algorithm instead of the naive k-nearest neighbor algorithm. The following 4 steps that have been illustrated in the diagram below outline the algorithm. |
| Step-1: Construct an appropriate set of positions/locations which can act as good candidates for insertion of new clusters; |
| Step-2: Initialize the first cluster as the mean of all the points in the dataset; |
| Step-3: In the Kth iteration, assuming K-1 clusters after convergence find an appropriate position for insertion of a new cluster from the set of points created in step-1that gives minimum distortion; |
| Step-4: Run k-means with K clusters till the convergence. Go back to Step3 if the required number of clusters is not yet reached. |
| The main operations in greedy k-nearest neighbor are to find the mean of points in a cluster region and to compute the distortion. While simply initially computing and storing the sum of all the points in a node can get the mean, Distortion can be determined by two ways, they are, |
| a. Computing Distortion for the current set of agent based centers |
| For all points X that is part of a specific center φ(x) the contribution to the total distortion is: |
distortion φ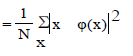 |
 (1) (1) |
| Where N is the number of points, The above equation can directly used to compute the distortion for the current set of count if one has stored the statistics of the sum of squared pattern of the count, the sum of the count which is belong to a single cluster and the number of count in each cluster. |
| b. Computing the distortion for the updated list of centers |
| The same statistics can be used to compute the distortion with the updated agent based centroids. This is a new method of computing the distortion devised by us. Let Φ’(x) be the new agent based centroids. ïÃÂæ’(x) is computed as the mean of the sum of count in each field. Thus |
 (2) (2) |
| Substituting the same in the equation (2), we get the following |
 (3) (3) |
| The statistics that need to be stored in either of these is the same way. That is sum of squared pattern of all the points in a node. After all, based on the rule that is used, we efficacy either obtain the distortion for the old set of centers or the one-step renovated centers. After that when we use the second formula for obtaining the distortion for the new cluster centers, the number of repetitions required for convergence would reduce by one (based on the criteria that we use for occurrences). This results in minimal reduction of the time taken for occurrences. The restricted filtering algorithm is highly efficient and faster than either the naive k-nearest neighbor algorithm or the filtering algorithm for all types of problems except when the dimensionality is very large. In fact, the restricted k-nearest neighbor algorithm can be viewed as a combination of the naïve k-nearest neighbor and the filtering algorithm. |
V.EXPIREMENTS AND RESULTS |
| A.Evaluation Metric |
| With the assumption of a global clustering for k-1 centers, we propose an systematic method to compute the global clustering for k clusters. As the global clustering for k = 1 is obvious (cluster center at the mean of all states), we can find the overall solution for k clusters initially. As the algorithm we present here can also be used for finding the minimum number of centers that satisfy a given formula. We also consider a number of real studies both on synthetic and real data. Overall, an insight has been achieved into the stability of MAS that make use of evolutionary agent, which is the first step in being able to control such systems. For example, one wanted to avoid a number of bad states on clustering. If the probability of being in those states kept changing with time, it would be difficult to devise a strategy to avoid these states. We then performed a stability analysis (similar to a sensitivity analysis) of a typical evolving agent population, by varying its key parameters while measuring its stability. We varied the mutation and crossover rates from 0% to 100% in 10% increments to provide a sufficient density of measurements to identify any trends that might be present, calculating the degree of instability, δ from, at the thousandth generation. This degree of instability values were averaged over 10,000 simulation runs to ensure statistical significance and graphed against the mutation and crossover rates. |
| B.Degree of Instability |
| As we design in the proposed model, research teams from various agent sites will be allowed to focus on data management areas such as usage data collection, data pre-processing, data mining algorithm design and implementation, and mined pattern interpretation, since data coming from different sites will be stored in a datacenter which is provided by cloud service providers. In addition, each team of researchers will set up their own monitoring systems and communication channels in order to build up appropriate study environments. The platform is designed to adopt a cloud agent based Service-Oriented Architecture (SOA) in order to facilitate the development and integration of heterogeneous database and application systems. If any team wants to access remote resources (data or applications), it merely requests web services through the SOA by applying the standardized programming grammar. This cloud based information sharing architecture can save much communication time, reduce cost, and preserve data security. |
| C.Stability Analysis |
| It shows that the crossover rate had little effect on the stability of the evolving agent population, whereas the mutation rate did significantly affect stability. With the mutation rate under or equal to 60%, the evolving agent population showed no instability, with δ values equal to zero as the system S was always in the same macro state M at infinite time, independent of the crossover rate. With the mutation rate above 60%, the instability increased significantly, with the system being in one of several different macro states at infinite time; with a mutation rate of 70%, the system was still very stable, having low δ values ranging between 0.08 and 0.16, but once the mutation rate was 80% or greater, the system became quite unstable, shown by high δ values nearing 0.5. |
 |
VI. CONCLUSIONS AND FUTURE WORKS |
| The evaluation result is to provide a greater understanding of strength in multi-agent systems that make use of evolutionary computing, i.e., evolving agent populations. As one would have expected, an extremely high mutation rate had a destabilizing effect on the stability of evolving agent populations. Also, as expected, the crossover rate had only a minimal effect, because variation from crossover was limited once the population matured, consisting of agents identical or very similar to one another. It should also be noted that the stability of the system is different to its performance at optimizing, because while showing no instability with mutation rates below 60% (inclusive), it reached the maximum macro state Mmax only with a mutation rate of 10% or above, while at 0% it was stable at suboptimal microstates’ between Mtenth (inclusive) and Mtwentieth (inclusive), i.e., with at least one individual with a fitness. For example, one wanted to avoid a number of bad states. If the probability of being in those states kept changing with time, it would be difficult to devise a strategy to avoid these states. However, if the probability converges in time, while one could not guarantee to avoid those states, one could at least calculate the expected damage, i.e., the probability of being in a state times by the penalty for being in it, summed over all the states one wishes to avoid. Stochastic control of MAS will be the subject of further work. Our future work will also consider including more experimental scenarios to further consolidate the conclusions, with a range of different fitness landscapes, including flat ones (from the neutral theory of molecular evolution) and ones with multiple global optima. |
References |
|