Research and Reviews - International Journals

International Journal of Innovative Research in Science, Engineering and Technology

Menu

ISSN ONLINE(2319-8753)PRINT(2347-6710)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Study on Graphs of Kinematic Chains

Dr. Ali Hasan
 Asst. Professor, Dept. of Mech. Engg., F/O-Engineering &Technology, Jamia Millia Islamia, New Delhi-110025, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Abstract

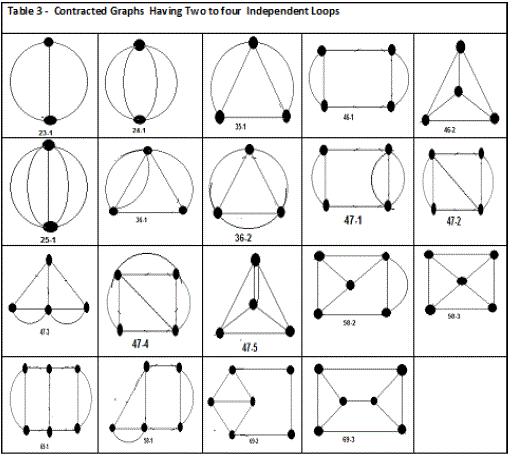
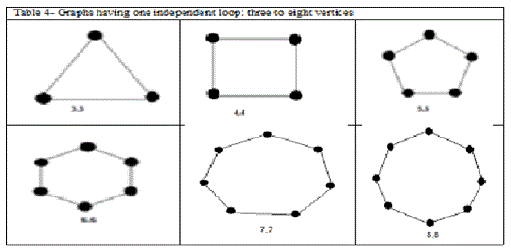
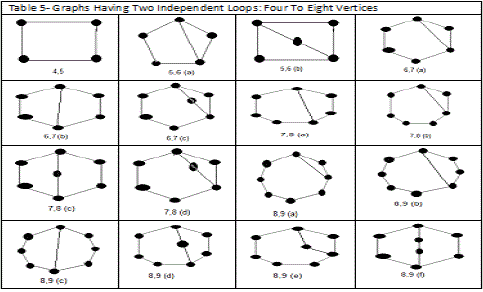
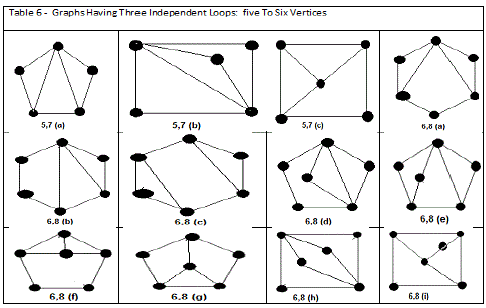
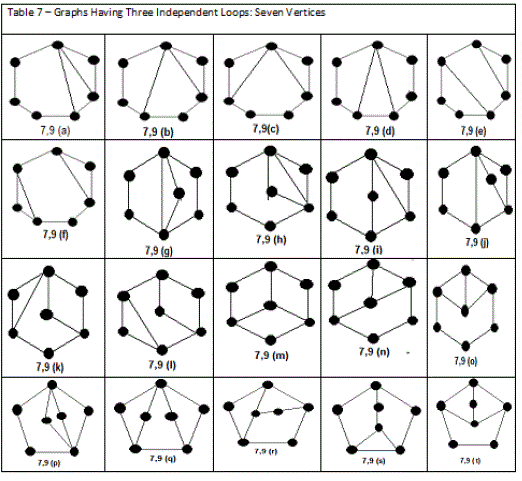
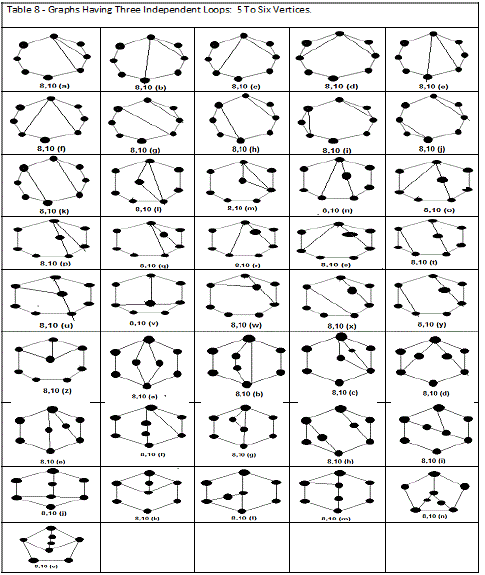
In this paper the author used graph theory and combinatorial analysis for enumeration of graphs of kinematic chains. Contracted graphs with up to four loops and six vertices are provided in Table 4. Based on the concept of expansion from contracted graphs, conventional graphs are generated. Conventional graphs with up to three independent loops and eight vertices are tabulated in Tables 5,6,7, and 8.. Using this collection, a large number of mechanisms can be developed by labelling the edges of the graphs according to the available joint types and the choice of fixed links.

Keywords
Kinematic chain, kinematic graphs or graph, contracted graphs, mechanisms.

INTRODUCTION
We know that the topological structures of kinematic chains can be represented by graphs. Several useful structural characteristics of graphs of kinematic chains were derived. In this paper we show that graphs of kinematic chains can be enumerated systematically by using graph theory and combinatorial analysis. There are a number of graphs but all of them are not suitable for construction of kinematic chains. Only graphs satisfying the structural characteristics are said to be feasible solutions. The following guidelines are framed to reduce the complexity of enumeration: 1. We are interested in closed-loop kinematic chains so, all graphs should be connected with a minimal vertex degree of 2. 2. All graphs should have no articulation points or bridges. 3. Only planar graphs are used here for the purpose of study. It has been shown that for the graph of a planar one-dof linkage to be non-planar, it must have at least 10 links according to Freudenstein [6]. Although there is no general theory for enumeration of graphs at this time, various algorithms have been developed [1, 2, 3, 4, 5, 14]. Woo [13] presented an algorithm based on contraction of graphs. Sohn and Freudenstein [10] employed the concept of dual graphs to reduce the complexity of enumeration (See also [9]). Tuttle et al. [11, 12] applied group theory. In this paper several methods for the enumeration of contracted graphs and graphs of kinematic chains have been introduced.

II. NOTATIONS USED
image

III. ENUMERATION OF CONTRACTED GRAPHS
Structural analysis means the study of the connection among the members of a mechanism kinematic chains and its mobility. Mainly, it is related with the fundamental relationships among the dof, number of links, number and the type of joints used in a mechanism. The structural analysis does not deal with the physical dimensions of the links. Mostly, graph theory is used as a helping tool in the study of the kinematic structure of mechanisms. The present study focused only on mechanisms whose corresponding graphs are planar and contain no articulation points or bridges. The topological structure of a mechanism kinematic chain is represented by a graph. The correspondence between the elements of a mechanism kinematic chain and that of a graph has been shown in Table 1 and Table 2.
image
As we know that a conventional graph can be transformed into a contracted graph by a process known as contraction. In a contracted graph, the number of vertices is equal to that of the conventional graph diminished by the number of binary vertices, vc= v − v2; the number of edges is also equal to that of the conventional graph diminished by the number of binary vertices, ec= e−v2; whereas the total number of loops remains unchanged, Lc= L. Since there are fewer vertices and edges in a contracted graph, enumeration of conventional graphs can be greatly simplified by enumerating an atlas of contracted graphs followed by an expansion of the graphs.

IV. SYSTEMATIC PROCEDURE FOR ENUMERATION OF CONTRACTED GRAPHS
To facilitate the study, the vertices of a graph are labeled sequentially from 1 to v. A vertex-to-vertex adjacency matrix, Ac, is defined as follows:
image

V. ENUMERATION OF CONVENTIONAL GRAPHS
Here we use a systematic enumeration methodology developed by Woo [13]. The method is based on the concept of expansion from contracted graphs. The procedure involves the following steps:
(a). Given the number of links and the number of joints, solve Equations (5) and (6) for all possible link assortments and each link assortment is known as a family. n2 + n3 + n4 +· · ·+nr = n---------------------------------------------(5) wherer = largest number of joints on a link. 2n2 + 3n3 + 4n4 +· · ·+rnr= 2j --------------------------------------- (6) (b). For each family, identify the corresponding contracted graphs from Table 3. (c). Solve Equations (7) and (8) for all possible combinations of binary link chains. We call each combination of binary link chains a branch. b1 + 2b2 + 3b3 +· · ·+qbq= v2, -------------------------------------------------(7) Where bi denotes the number of binary strings of length i, and q denotes the longest binary string in a conventional graph. We may consider a binary string of zero length as a special case in which two vertices of degree greater than two are connected directly by an edge. From the definition of a contracted graph, it follows that b0 + b1 + b2 + b3 +· · ·+bq= ec .------------------------------------------(8) (d). Permute the edges of each contracted graph with each combination of binary link chains obtained in (c) in as many arrangements as possible. This is equivalent to the problem of coloring the edges of a graph. Here, the concept of similar edges can be employed to reduce the number of permutations. (e). Eliminate those graphs that contain either parallel edges or partially locked sub-chains. (f). Check for graph isomorphism. Note that only those graphs that belong to the same family and same branch can possibly be isomorphic to one another.

VI. ILLUSTRATIVE EXAMPLES
image
image
image
Next, we find the corresponding contracted graphs and solve Equations (7) and (8) for all possible partitions of binary links. Since we are interested in F = 1 kinematic chains, the length of any binary link chain is bounded by q ≤ 2 as the upper boundon the length of a binary link chain 2400 family: For the 2400 family, the corresponding contracted graphs have vc= 6 − 2 = 4 vertices and ec= 8 − 2 = 6 edges. There are two contracted graphs with 4 vertices and 6 edges as shown in Figure 3. With n2 = 2, ec= 6, and q = 2, b1 + 2b2 = 2, -------------------------------------------------(23) b0 + b1 + b2 = 6. ----------------------------------------------(24) Solving Equation (23) for nonnegative integersb1 and b2, and then Equation (24) for b0 yields two branches of binary link chains:
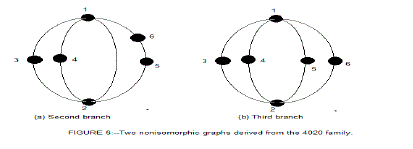
image
For the first branch, we replace two of the four parallel edges of the contracted graph shown in Figure 1 each with a binary link chain of length two. This produces no feasible solutions because the resulting graphs always contain two parallel edges. For the second branch, we replace two of the four edges of the contracted graph each with a binary link chain of length one and one with a binary link chain of length two. For the third branch, we replace all four edges of the contracted graph each with a binary link chain of length one. As a result, we obtain two non-isomorphic graphs as shown in Figure 6.
image

VII. CONCLUSIONS
We have shown that systematic algorithms using graph theory and combinatorial analysis can be developed for enumeration of graphs of kinematic chains. Contracted graphs with up to four loops and six vertices are provided in TABLE 4. Based on the concept of expansion from contracted graphs, an algorithm for enumeration of conventional graphs is explained. Conventional graphs with up to three independent loops and eight vertices are tabulated in Tables 4,5,6,7, and 8. Using these collection, an enormous number of mechanisms can be developed by labeling the edges of the graphs according to the available joint types and the choice of fixed links. All graphs given in Tables 4,5,6,7, and 8 are sketched in such a way that the longest circuit forms the peripheral loop and the vertex of highest degree appears on the top (or upper-left corner), provided that it does not cause crossing of the edges.These graphs are arranged in the order of complexity according to the number of loops, number of vertices, and length of peripheral loop.
image
image
image
image
image
image

References
  1. Chang, S.L. and Tsai, L.W., 1990, Topological Synthesis of Articulated Gear Mechanisms, IEEE Journal of Robotics and Automation, 6, 1, 97– 103.
  2. Chatterjee, G. and Tsai, L.W., 1994, Enumeration of Epicyclic-Type Automatic Transmission Gear Trains, SAE 1994 Trans., Journal of Passenger Cars, Sec. 6,103, 1415–1426.
  3. Crossley, F.R.E., 1964, A Contribution to Grübler’s Theory in Number Synthesis of Plane Mechanisms, ASME Journal of Engineering for Industry, Series B,86, 1–8.
  4. Crossley, F.R.E., 1965, The Permutation of Kinematic Chains of Eight Members or Less from the Graph-Theoretic Viewpoint, in Developments in Theoretical and Applied Mechanics, Vol. 2, Pergamon Press, Oxford, 467–486.
  5. Davies, T.H., 1968, An Extension of Manolescu’s Classification of Planar Kinematic Chains and Mechanisms of Mobilitym≥ 1, Using Graph Theory, Journal of Mechanisms and Machine Theory, 4, 87–100.
  6. Freudenstein, F., 1967, The Basic Concept of Polya’s Theory of Enumeration with Application to the Structural Classification of Mechanisms, Journal of Mechanisms, 3, 275–290.
  7. Pólya, G., 1938, KombinatorischeAnzahlbestimmungen ´f’urGruppen,Graphen und ChemischeVerbindungen, Acta Math., 68, 145–254.
  8. Read, R.C. and Wilson, R.J., 1998, An Atlas of Graphs, Oxford University Press, New York.
  9. Ali Hasan, 2007 “Some Studies On Characterization and Identification of Kinematic Chains and Mechanisms”, Ph.D. Dissertation, Dept. of Mechanical Engineering,,JamiaMilliaIslamia, New Delhi, India.
  10. Sohn,W. and Freudenstein, F., 1986, An Application of Dual Graphs to the Automatic Generation of the Kinematic Structures of Mechanism, ASME Journal of Mechanisms, Transmissions, and Automation in Design, 108, 3, 392–398.
  11. Tuttle, E.R., Peterson, S.W., and Titus, J.E., 1989, Enumeration of Basic Kinematic Chains Using the Theory of Finite Groups, ASMEJournal of Mechanisms,Transmissions, and Automation in Design, 111, 4, 498–503.
  12. Tuttle, E.R., Peterson, S.W., and Titus, J.E., 1989, Further Application of Group Theory to the Enumeration and Structural Analysis of Basic Kinematic Chains, ASME Journal of Mechanisms, Transmissions, and Automation in Design, 111, 4, 494–497.
  13. Woo, L.S., 1967, Type Synthesis of Plane Linkages, ASME Journal of Engineering for Industry, Series B, 89, 159–172.
  14. Yan, H.S., 1998, Creative Design of Mechanical Devices, Springer-Verlag,Singapore.