Sum Query Evaluation over Uncertain Data

Roslinmary M; Saravana Kumar T; Addlin Shinney R

Sum Query Evaluation over Uncertain Data

Roslinmary M¹, Saravana Kumar T ² and Addlin Shinney R ³

M.TECH / IT, Dr.Sivanthi Aditanar College of Engineering, Tiruchendur-628215, Tamilnadu, India
Asst. Prof / IT, Dr.Sivanthi Aditanar College of Engineering, Tiruchendur-628215, Tamilnadu, India

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering

Abstract

One of the important Queries in Many real time applications is SUM query, it deals with unpredictable data. In this paper, dealing with the query, called ALL_SUM Query. In general, the SUM query returns only the sum of the values. But the ALL_SUM Query returns all possible sum values together with their probabilities. There is no efficient solution for the problem of evaluating ALL_SUM queries used in many applications where the aggregate attribute values are real with small precision. In this paper, evaluating a pseudo - polynomial algorithm called DPSUM algorithm which is based on a recursive approach, it efficiently calculate ALL_SUM Query. The proposed DPSUM algorithm returns an efficient solution for determining the exact result of ALL_SUM queries. The results of an experimental evaluation over synthetic and real-world data sets show its effectiveness.

Keywords

query processing, Database management systems

INTRODUCTION

Uncertain Database is “Membership of an item to the database” is a probabilistic event or the value of attributes is a probabilistic variable. Uncertain data streams are important in growing number of environments, such as traditional sensor networks, RFID networks for object tracking, radar networks for severe weather monitoring and etc.Aggregate query, in particular SUM queries, are essential for many applications that deal with uncertain data. Let us give a motivating example from the medical applications domain.

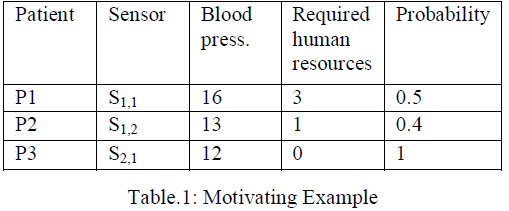Example: E-health Management System. Consider a medical canter that monitors key biological parameters of remote patients at their homes, using sensors in their bodies. The sensors periodically send to the canter the patients health data, e.g. blood pressure, hydration levels, thermal signals, etc. For high availability, there are two or more sensors for each biological parameter. However, the data sent by sensors may be uncertain, and the sensors that monitor the same parameter may send inconsistent values as shown in table.1. There are approaches to estimate a confidence value for the data sent by each sensor, e.g. based on their precision. According to the data sent by the sensors, the medical application computes the number of required human resources, e.g. nurses, and equipments for each patient. One important query in this application is “return the sum of required nurses”. Table.1 shows an example table of this application. The table shows the number of required nurses for each patient.

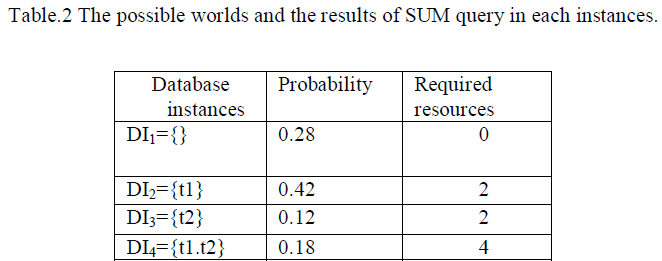
The table.2 shows the possible worlds, i.e., the possible database instances, their probabilities, and the result of the SUM query in each world. In this example, there are eight possible worlds and four possible sum values, i.e., 0 to 3.

A Navie algorithm for evaluating ALL_SUM queries is to return all possible worlds, i.e. .all possible database instances, compute sum in each world, and return the possible sum values and their probability. However, Search space can be exponential - Up to 2n answers for SUM queries, where n is the number of uncertain items.In this demonstration, we present a probabilistic database system for managing uncertain data.Our demonstration application is the E- health Management system application described in above Example.

The rest of the paper is organized as follows. In Section 2, we present some technical basis e.g. the probabilistic data models and some intuitions about our algorithms. In Section 3, we describe our Algorithm. In Section 4 we present performance evaluation of my paper. Section 5 concludes.

TECHNICAL BASIS

In this section we introduce the probabilistic data models that we consider. Main objective for using Probabilistic database is to extend data management tools to handle probabilistic data. Then, we define the problem that we address.

2.1 Probabilistic Models

we first introduce the two probabilistic data models that most frequently used in our community.

Tuple-level model:

In this model, each uncertain table T has an attribute that indicates the membership probability (also called existence probability) of each Tuple in T, i.e., the probability that the Tuple appears in a possible world. In this paper, the membership probability of a Tuple ti is denoted by p(ti). Thus, the probability that ti does not appear in a random possible world is 1-p(ti). The database shown in Table.3 is under Tuple-level model.

Attribute-level model:

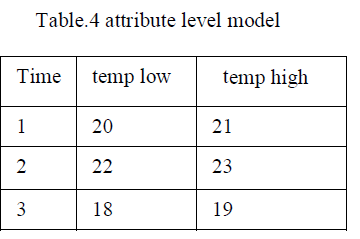
In this model, each tuple ti has at least one uncertain attributes, e.g. α, and the value of α in ti is chosen by a random variable X. assume that X has a discrete probability density function(pdf). This is a realistic assumption for many applications e.g., sensor readings.

2.2 Problem Definition

ALL_SUM Query:

It returns all possible sum results together with their probability. Let us now formally define ALL_SUM queries. Let D be a given uncertain database, W the set of its possible worlds, and P(w) the probability of a possible world w ∈ W. Let Q be a given aggr query, f the aggr function stated in Q (i.e., SUM), f(w) the result of executing Q in a world w ∈ W, and VD,f the set of all possible results of executing Q over D, i.e., VD,f = { ;/∃ ∈ ^ ;(&) = ; }. The cumulative probability of having a value v as the result of Q over D, denoted as P (v, Q , D), is computed as follows:

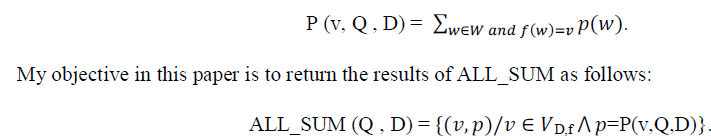Q_PSUM AND DPSUM ALGORITHM

In this section, proposed an efficient solution for evaluating ALL_SUM queries. Here first propose a new recursive approach for computing the results of ALL_SUM. Then, using the recursive approach propose the Q_PSUM algorithm and DPSUM algorithm. Here use that the database is under the tuple-level model and attribute-level model.

3.1 ALL_SUM Under Tuple - Level Model

In this section propose an efficient solution for evaluating ALL_SUM queries. first propose a new recursive approach for computing the results of ALL_SUM. Then, using the recursive approach propose an Q_PSUM algorithm. Assume that the database is under the tuple-level model defined in the previous section.

3.1.1 Recursive Approach

First develop a recursive approach that produces the results of ALL_SUM queries in a database with n tuples based on the results in a database with n - 1 tuples. The principle behind it is that the possible worlds of the database with n tuples can be constructed by adding/not adding the nth tuple to the possible worlds of the database with n -1 tuples. Let be a database involving the tuples t1, . . . , tn, and ps(i,n) be the probability of having sum = i in , then develop a recursive approach for computing ps(i; n).

3.1.2 DPSUM Algorithm

In this section, using the dynamic programming technique, propose an efficient algorithm, called DPSUM, designed for the applications where aggr values are integer or real numbers with small precisions. It is usually much more efficient than the Q_PSUM algorithm. Let MaxSum be the maximum possible sum value, e.g., for positive aggr values MaxSum is the sum of all values. DPSUM uses a 2D matrix, say PS, with (MaxSum + 1) rows and n columns. DPSUM is executed on PS, and when it ends, each entry PS[i, j] contains the probability of sum = i in a database involving tuples t1 . . . . .tj..

DPSUM proceeds in two steps as follows

1. In the first step, it initializes the first column of the matrix This column represents the probability of sum values for a database involving only the tuple t1. DPSUM initializes this column using the base of recursive formula as follows:

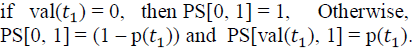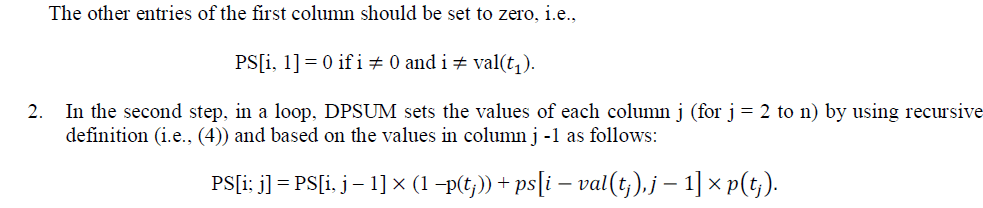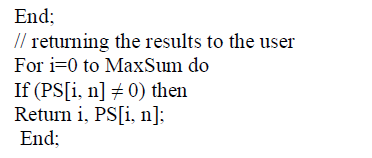3.2 ALL_SUM Under Attribute-Level Model

Due to the significant differences between the tuple-level and the attribute-level models it is not trivial to adapt yet proposed algorithms for the attribute-level model. In this section, proposed solution for computing ALL_SUM results under the attribute-level model.

Recursion Step

DPSUM2 Algorithm

Now, describe a dynamic programming algorithm, called DPSUM2, for computing ALL_SUM under the attributelevel model. Here, similar to the basic version of DPSUM algorithm, assume integer values. However, in a way similar to that of DPSUM, this assumption can be relaxed. Let PS be a 2D matrix with (MaxSum + 1) rows and n columns, where n is the number of tuples and MaxSum is the maximum possible sum, i.e., the sum of the greatest values of aggr attribute in the tuples. At the end of DPSUM2 execution, PS[i ,j] contains the probability of sum = i in a database involving tuples ti, . . . .tj.

DPSUM2 works in two steps.

1. In the first step, it initializes the first column of the matrix, by using the base of the recursive definition, as follows: for each possible aggr value of tuple t1, e.g., vl,k, it sets the corresponding entry equal to the probability of the possible value, i.e., it sets P[vl,k , 1]= Pl,k for 1 <= k <= m.

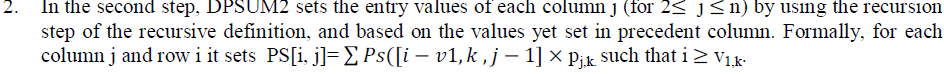Let us now analyze the complexity of the algorithm. Let avg = MaxSum/n, i.e., the average of the aggregate attribute values. The space complexity of DPSUM2 is exactly the same as that of DPSUM, i.e., O (n2 × avg). The time complexity of DPSUM2 is O(MaxSum × n × m). In other words its time complexity is O ( m × n × avg ).

CONCLUSION

One of the important Query in Many real time applications is SUM query, it deals with unpredictable data. In this paper, dealing with the query, called ALL_SUM Query. In this paper, evaluating a pseudo - polynomial algorithm called DPSUM algorithm which is based on a recursive approach, it efficiently calculate ALL_SUM Query. It returns exact result of ALL_SUM queries. The results of an experimental evaluation over synthetic and real-world data sets show its effectiveness of our solution. The performance of DPSUM is better than Navie Algorithm.

References

T.S. Jay ram, A. McGregor, S. Muthukrishnan, and E. Vee, “Estimating Statistical Aggregates on Probabilistic Data Streams,” Proc. 26th ACM SIGMOD-SIGACT-SIGART Symp. Principles of Database Systems (PODS), 2007.
C. Re´ and D. Suciu, “Efficient Evaluation of HAVING Queries on a Probabilistic Database ,” VLDB J.—Int’l J. Very Large Data Bases, vol. 18, no. 5, pp. 1091-1116, 2009.
N. Dalvi and D. Suciu, “Efficient Query Evaluation on Probabilistic Databases,” VLDB J.—Int’l J. Very Large Data Bases, vol. 16, no. 4, pp. 523-544, 2007.
A. Gal, M.V. Martinez, G.I. Simari, and V. Subrahmanian, “Aggregate Query Answering under Uncertain Schema Mappings,” Proc. Int’l Conf. Data Eng. (ICDE), 2009.
T. Tran, A. McGregor, Y. Diao, L. Peng, and A. Liu, “Conditioning and Aggregating Uncertain Data Streams: Going Beyond Expectations,” Proc. Int’l Conf. Very Large Data Bases (VLDB), 2010.
G. Rempala and J. Wesolowski, “Asymptotics of Products of Sums and U-statistics,” Electronic Comm. in Probability, vol. 7, pp. 47-54, 2002.
B. Ross, V.S. Subrahmanian, and J. Grant, “Aggregate Operators in Probabilistic Databases,” J. ACM, vol. 52, no. 1, pp. 54-101, 2005.
R. Gupta and S. Sarawagi, “Creating Probabilistic Databases from Information Extraction Models,” Proc. 32nd Int’l Conf. Very Large Data Bases (VLDB), 2006.
L. Antova, T. Jansen, C. Koch, and D. Olteanu, “Fast and Simple Relational Processing of Uncertain Data,” Proc. IEEE 24th Int’l Conf. Data Eng. (ICDE), 2008.
G. Cormode, F. Li, and K. Yi, “Semantics of Ranking Queries for Probabilistic Data and Expected Ranks,” Proc. 22nd Int’l Conf. Data Eng. (ICDE), 2009.
D. Burdick, P. Deshpande, T.S. Jayram, R. Ramakrishnan, and S.Vaithyanathan, “OLAP over Uncertain and Imprecise Data,” Proc. 31st Int’l Conf. Very Large Data Bases (VLDB), 2005.
G. Cormode and M.N. Garofalakis, “Sketching Probabilistic Data Streams,” Proc. ACM SIGMOD Int’l Conf. Management of Data (SIGMOD), 2007.