ISSN ONLINE(2320-9801) PRINT (2320-9798)
ISSN ONLINE(2320-9801) PRINT (2320-9798)
| B.Shibi1 P.G Student, Department of Computer Science and Engineering, V.S.B Engineering College, Karur, Tamilnadu, India |
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering
Utility mining emerges as an important topic in data mining field. Here high utility item sets mining refers to importance or profitability of an item to users. Efficient mining of high utility itemsets plays an important role in many real-life applications and is an important research issue in data mining area. Number of Algorithms utility pattern growth (UP-Growth) and UP-Growth+,.( A data structure having tree like structure named utility pattern tree (UP-Tree)) is used for storing the information about high utility itemset such that by using only double scanning of database, candidate itemsets can be efficiently generate. But that will lead to high requirement of space and time and so that performance will be less. So a new algorithm is proposed in this paper, for efficient discovering of high utility itemsets from transactional database.
Keywords |
| utility pattern growth, systolic tree, high utility itemsets |
INTRODUCTION |
| Utility pattern growth (UP-Growth) and UP-Growth+ will determine the high utility itemset from transactional database by using only two scan of database ,but Two drawbacks prevent a more widespread of this algorithm. the first is high requirement of space second is space requirement. Systolic tree will solve this problem. A systolic tree is an arrangement of pipelined processing elements (PEs) in a multidimensional tree pattern. The goal of our architecture is to mimic the internal memory layout of the FP-growth algorithm while achieving a much higher throughput. The role of the systolic tree as mapped in FPGA hardware is then similar to the FP-tree as used in software. The formal definition of FPtree can be found in supplementary. |
| The design principle of the WRITE mode algorithm is that the built-up systolic tree should have a similar layout with the FP-tree given the same transactional database. The software sends a candidate pattern to the systolic tree. After some clock cycles, the systolic tree sends the support count of the candidate pattern back to the software. The software equivalences the support count with the support threshold and decides whether the candidate pattern is frequent or not. After all candidate patterns are compared with the support threshold in software, the pattern mining is done. The method to get the support count of a candidate pattern is called candidate item set (pattern) matching. |
BACKGROUND |
| Here we are discussing some basic definitions about utility of an item, utility of itemset in transaction, utility of itemset in database and also related works and define the problem of utility mining and then we will introduce related strategies. |
| A Preliminary |
| Given a finite set of items I={i1,i2,i3…im }each item ip(1≤p≤m) has a unit profit pr(ip). An itemset X is a set of k distinct items I={i1,i2,i3…ik } , where ij I,1≤j≤k. k is the length of X. An itemset with length k is called a k itemset. A transaction database D ={T1; T2; . . . ; Tn } contains a set of transactions, and each transaction Td( 1≤d≤n) has a unique identifier d, called TID. Each item ip in transaction Td is associated with a quantity q(ip,Td), that is, the purchased quantity of ip in Td. |
| Definition 1.Utility of an item ip in a transaction Td is denoted as u(ip,Td) and defined as pr(iP)×q(ip,Td) |
| Definition 2.Utility of an itemset X in Td is denoted as U(x,Td) and defined as ΣipâÃâ¹Ã´X∨X⊆Tdu(ip,Td) |
| Definition 3.Utility of an itemset X in D is denoted as u(X)andΣX⊆Td∧Td⊆Du(X,Td) |
| Definition 4.An itemset is called a high utility itemset if its utility is no less than a user-specified minimum utility threshold or low-utility itemset represented by min-util. |
| Utility mining emerges as an important topic in data mining field. Mining high utility itemsets from databases refers to finding the itemsets with high profits. Here, the meaning of itemset utility is interestingness, importance, or profitability of an item to users. Items’s utility in a transaction database consists of two aspects: |
| 1) The importance of distinct items, which is called external utility. |
| 2) The importance of items in transactions, which is known as internal utility. |
| Utility of an itemset is defined as the product of its external utility and its internal utility. An itemset is called a high utility itemset if its utility is no less than a user-specified minimum utility threshold; otherwise, it is called a low-utility itemset. |
| Existing system propose two novel algorithms as well as a compact data structure for efficiently discovering high utility itemsets from transactional databases. Major contributions of this work are summarized as follows: |
| 1. Two algorithms, named utility pattern growth (UPGrowth) and UP-Growth+, and a compact tree structure, called utility pattern tree (UP-Tree), for discovering high utility itemsets and maintaining important information related to utility patterns within databases are proposed. High-utility itemsets can be generated from UP-Tree efficiently with only two scans of original databases. |
| 2. Several strategies are proposed for facilitating the mining processes of UP-Growth and UP-Growth+ by maintaining only essential information in UP-Tree. By these strategies, overestimated utilities of candidates can be well reduced by discarding utilities of the items that cannot be high utility or are not involved in the search space. The proposed strategies can not only decrease the overestimated utilities of PHUIs but also greatly reduce the number of candidates. |
B Drawbacks |
| 1. The UP-Tree algorithm stores all transactions in the database as a tree using two scans. |
| 2. It occupy the lot of memory |
| 3. Tree searching process is slow |
RELATED WORKS |
| Eventhough Algorithms utility pattern growth (UP-Growth) and UP-Growth is used for storing the information about high utility itemset such that by using only double scanning of database, candidate itemsets can be efficiently generate. But that will lead to high requirement of space and time and so that performance will be less. So a new algorithm is proposed in this paper that is discovering high utility itemsets from transactional databases by using systolic tree. |
| A Data Structure |
| It is not always practical or efficient to directly translate a software algorithm into a hardware architecture. Our approach is to build the tree based on the maximum node degree estimation. When the actual node degree at some point in the tree exceeds the estimated node degree, some frequent itemset will not be found. Suppose the number of items in the database is n, the estimated maximum node degree estimation is K and the estimated depth of the systolic tree is W. Each node in the static tree structure has K children .The total number of nodes in the tree is KW +KW−1+...+K1 = K(KW−1)K−1 . When K is large, the number of children for each node is large which in turn requires each node to have a large number of interfaces. This will make the inner structure of each node very complex. To simplify the complexity of the node, we assign two instead of K interfaces to each node. One of the two interfaces is dedicated to the connection with its first child, the other one is connected to its nearest sibling. This FP-tree is different from the one defined in [2] in that it has a control node. The input and output of the whole systolic tree passes through the control node. The input can be be anything such as data or control signal and the output is usually defined by the designer. The letter inside each node represents the item, and the number beside the node is the number of times that the item emerges in the transaction database. The dashed lines indicate the connections in the original FP-tree. The solid lines show the actual connections of the nodes in the systolic tree .Figure 2 shows the static systolic structure where K=2and W=3. Each node in the systolic tree architecture is also referred to as a processing element (PE). Each PE has its local data structure and corresponding operations upon receiving signals from outside. There are three kinds of processing elements in this figure. |
 |
| The root PE is the control node discussed above. The PEs in the rightmost column are the counting nodes which are specifically used for frequent itemset dictation, |
| The third kind of processing elements are the general PEs. Each node in Fig. 1 has a counterpart in the general processing elements I n Fig. 2, but the converse does not hold. Each general PE has one input from its parent and two outputs to its child and siblings respectively. Each PE only has a connection with its leftmost child. If it has to send the data to its rightmost child, the data will be passed to its leftmost child and then through to all children on the way through its siblings. The general processing elements which do not contain any item are empty. If the items in one transaction are transferred into the architecture in an ascending order, any PE must contain a smaller item than that of its children. However this does not guarantee that the node item in the systolic tree is always greater than its left-side siblings. |
| B Systolic Tree Creation |
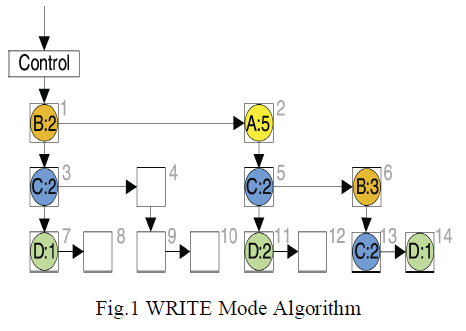
| Each PE in the systolic tree has three modes: WRITE mode, SCAN mode and COUNT mode. The last two modes will be discussed in later sections. When the tree is in building phase, PEs are in WRITE mode. An item is loaded into the control PE each cycle which in turn transfer each item into the general PEs. If PE contain an item already, the corresponding count value will be increased. Otherwise, an appropriate empty PE will be located for it. The algorithm for WRITE mode in each PE is given in Fig. 3. The input of the algorithm is an item t. The match flag is set when the item in PE matches t. The Inpath flag is not set when the PE does not contain any item of the current transaction. For example, the PE under the control PE in Fig. 2 should not contain the item B in a new transaction {A,B,C}. After all items are sent to the systolic tree, a control signal that represent the end of an old transaction and the start of an ew one is sent to the control PE. The signal will be broadcasted to all PEs which reinitialize themselves for the next transaction. |
 |
| Let’s illustrate the creation of systolic tree with an example shown in Fig. 1. In order to distinctly distinguish PEs a number in light scale is placed in the top-right corner. Suppose a new transaction A,B,D is to be added into the systolic tree. A control signal which indicates the WRITE mode is first broadcasted from the control PE. Then the transaction A,B,D is sent to the control PE sequentially. When PE1receives A, the step (3) in Fig. 3 is triggered and A is forwarded to PE2. The Inpath flag in PE1 is set to 0. Step (2)is triggered in PE2. The count value in PE2 is increased by1. The match flag is set to 1. PE2 stops forwarding A to otherneighboring. While item A is passed to PE2 by PE1, the second item B is sent to PE1 by the control node. Step (3)is triggered in PE1. Item B is sent to PE2. Since the match f lag is set to 1, the item B is sent to PE5. Next, step (3) is triggered in PE5. B is then sent to PE6 where it is not further forwarded. The count value is increased by 1 in PE6. In a similar way, the item D is sent to PE14. |
C Candidate Itemset Dictation |
| The FP growth algorithm generates frequent itemsets by recursive enumeration. However, a recursive implementation is impractical in an FPGA implementation. The approach used in systolic tree architecture is what we call candidate itemset dictation. When we want to check whether a given itemset is frequent or not, it is sent to the systolic tree. The number of the itemset will be obtained in the output of the systolic tree after some clock cycles. The dictation must be performed after the systolic tree is built. When the tree is in itemset dictation phase, PEs are in SCAN mode. In our systolic tree structure there is only one path trace algorithm. |
| Algorithm: SCAN mode(item t) |
| open the bottom door; |
| match := 0; IsLeaf := 0; |
| (1)if PE is empty then |
| stop forwarding; |
| (2)if (t is in PE) and (Bottom door is open) then |
| match := 1; |
| IsLeaf := 1; |
| forward t to the sibling; |
| (3)if t < the item in PE then |
| IsLeaf := 0; |
| close the bottom door; |
| forward t to the sibling; |
| (4)if t > the item in PE then |
| IsLeaf := 0; |
| forward t to the sibling; |
| forward t to the child if the bottom door is open |
| The main principle of dictation is that any path containing the queried candidate itemset will be reported to the control node. Note that such path may contain more items than the queried itemset. To clarify the dictation algorithm, we deem there are two doors in each PE. The right door is always open. The bottom door is locked when no data should be sent to the children. The door policy is described in Fig. 4.The IsLeaf flag is set if PE matches the last item in the queried candidate itemset. The PE with IsLeaf set is responsible for reporting the number of the candidate itemset to the counting PEs. Since the item is sent one by one, the flag IsLeaf is cleared if another item in the candidate itemset which is larger than the stored item passes through the PE. If the input item is smaller than the stored item, the bottom door should be closed. The rationale behind this is that the item in the child can never be larger than that of its ancestor in a path. Whenever a bottom door in a PE is closed, the path passing through it will never contain the candidate itemset. However if the input item is larger than the stored item, it should be forwarded to all open doors. The rationale is that the path may contain items which are not in the candidate itemset and the candidate itemset is contained in the path. Let’s illustrate the whole dictation process with the example shown in Fig. 5. Suppose the threshold support count is four. Now we want to check whether the candidate itemset {B,D} is frequent. A control signal which indicates the SCAN mode is first broadcasted from the control PE. Then the item B is sent to the control PE. When PE1 receives B ,the step (2) in Fig. 4 is triggered and B is forwarded to PE2(figure) Upon receiving the item B, the step (4) is triggered. The bold lines show the track of the item B. PE5 closes the bottom door and forwards the item to PE6. The bottom door inPE5 is locked. At this moment both PE1 and PE6 have the IsLeaf flag set. Now take the item D which is sent one clock cycle later after the item B is sent in a pipelined fashion. When PE1 receives the item D, the step (4) is triggered in Fig. 4. The IsLeaf flag is cleared and D is forwarded to PE3 and PE2. The dashed lines represent the root taken by item D. Notice that since the bottom door of PE5 is lockedPE11 will not receive the item D. The IsLeaf flag in PE6 is cleared upon receiving D. In the end the IsLeaf flag is set in PE7 and PE14. As will be explained in the following section, these two PEs report their item count to the counting node. The item count value in both PE7 and PE14 is one. The total count of candidate itemset {B,D} is two .So that this candidate itemset is not frequent one. |
D Candidate Itemset Count Computation |
| Once all items in a candidate itemset are sent to the systolic tree, the COUNT mode is signified by control signal broadcasted to the whole systolic tree. The architecture of the systolic tree will change accordingly with response to the COUNT mode signal. at Fig. 2, we have represented that the input interface of first childis always connected to its parent while others accept input from the first child in WRITE and SCAN mode. In COUNT mode, all PEs receive input from its leftmost neighbor except each row’s first PE. The PEs with IsLeaf flag set are prepared to send their own item count and forward the count from their leftmost neighbor in a pipelined fashion when all PEs are in COUNT mode. The counting PEs on the rightmost column always enter the COUNT mode earlier than the general PEs. This is different from the operation used in WRITE mode or SCAN mode where the items are sent one by one in each clock cycle. The COUNT mode control signal sent to the counting PEs by the control PE should at least be delayed(KW − W) cycles after it is sent to the general PEs. |
| The Algorithm: |
| COUNT mode(int number) |
| CountSent := 0; |
| if (CountSent = 0) and (IsLeaf = 1) then |
| CountSent := 1; |
| forward (count + number) to its neighbor; |
| else |
| forward (number) to its neighbor |
| COUNT mode algorithm in each PE is listed in Fig. 6.The input of the algorithm is an integer sent by its left neighbor. The count variable is the number of the locally stored item. The CountSent flag is set when the local number has been reported to the counting PEs. Only the PEs with the IsLeaf flag set can report its local count value while other PEs transfer the number sent by the left neighbor to the right neighbor. The counting PEs transfer the number sent by its left and bottom neighbors to its top neighbor. The control PE adds up all number sent by the counting PEs and sends it to the output signal. |
E Candidate Itemset Generation |
| The FP-growth algorithm uses a divide and conquer approach to generate frequent itemset by searching the tree in a bottom up fashion. From the hardware perspective, the candidate generation method used in apriori is more suitable for dictation .There are several candidate generation procedures .The Fk−1×Fk−1 method is well suited for systolic tree [12].A new candidate itemset with k items is dictated only if it is generated from two frequent itemsets with k−1 items whose first k − 2 items are identical. This approach will decrease the number of candidate itemset dramatically. |
IMPLEMENTATION EVALUATION |
A Simulated Result |
| The systolic tree architecture was simulated and synthesized in ISE 9.1.03i on target board Xilinx Virtex5 XC5VLX330.The performance and area requirement results in Table 2 are extracted from the post place and route report. The total number of PEs includes control PE and counting PEs. The biggest circuit in the table is 25% of the device since the area usage is exponentially related to the value of W and K while the clock frequency decreases very slightly with the increase of W and K. The control signal and data width is eight bits in our system. The throughput is around3Gbps. Remember that to build the systolic tree the items in transactional database are sent to the tree one by one in each clock cycle. The time required to build the systolic tree is |B| throughput seconds where |B| is the size of the database in bits. |
| B Mining Time Comparison |
| To find all frequent itemsets, we can dictate all candidate frequent itemsets. If a transaction database has n items, the total number of candidate frequent itemsets is 2n. A database can be divided into multiple sub-databases with a smaller number of items [2]. These sub-databases can be mined in a parallel manner. The parallel manner is also called “Parallel Projection” where all sub-databases are mined simultaneously. The time for creating systolic tree and transferring data through I/O device is usually trivial compared with the time for mining .To check the support count of a candidate itemset, the C items are sent to the systolic tree in a pipelined fashion .It takes C cycles in the WRITE mode. The time in SCAN mode is for an item propagated from the control node to the furthest node. Since each node has K degrees and the depth of the tree is W, it takes (K − 1) × W cycles. In COUNT mode the support count is collected from those nodes where the last item in the candidate itemset resides. This includes the time for the general node propagating the support count to the counting node in the same row and the time for the counting node to propagate the support count to the control node. The runtime for the former case is determined by the characteristic of the database. Suppose the database has n frequent items. Not every candidate itemset will be produced by the Fk−1 × Fk−1 method with equal probability .In general the probability of a candidate with k items isCkn2n .Each node in the systolic tree has the equal possibility to be the reporting nodes. The average time to dictate the 2ncandidates for the former case is 12n ×_nk=1 nkCkn .The latter in the worst case is W cycles which is the time for the bottom counting node to propagate the item to the control node. The time in this part is negligible compared with that of the former case computed above. For an arbitrary transactional database with n frequent items ,it can always be projected into multiple sub-databases with N frequent items by Parallel Projection. Since these sub databases are mined in parallel, the time required for mining is solely determined by the size of the systolic tree. If the size of the tree N is equal to the number of frequent items n, i.e, K = W = N = n, the number of clock cycles for mining are 2n ×_nk=1 nkCkn. Based on the simulated result, we compare the mining time of systolic tree with FP-growth algorithm in Fig. 7.The FP-growth algorithm is from [13]. The mining time of the software algorithm is collected from a PC with Pentium D 3GHz CPU, 2GB RAM. The benchmark is chess .dat from [14] which is prepared from the UCI datasets and PUMSB .This database has 75 items and 3196 transactions. |
CONCLUSION |
| In this paper we proposed a systolic tree hardware architecture for utility mining. Similar to the UP-growth algorithm, our architecture only requires two database reads .Our preliminary experiments show that with the careful selection of the size of the systolic tree, the mining time can be greatly accelerated compared to current software approaches. |
References |
|