ISSN ONLINE(2320-9801) PRINT (2320-9798)
ISSN ONLINE(2320-9801) PRINT (2320-9798)
S.Charanyaa1, K.Sangeetha2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering
A big deal of research has been performed in the area of graphical data anonymization. Because of the wide range of application of graphical data from social network data to large warehouse data and knowledge engineering domains. Notion of k-anonymity has been proposed in literature, which is a framework for protecting privacy, emphasizing the lemma that a database to be k-anonymous, every tuple should be different from at least k-1 other tuples in accordance with their quasi-identifiers(QIDs). Inspite of the existence of k-anonymity framework, malicious users and misfeasers may get authorization to the sensitive information if a set of nodes exhibit alike attributes. In this paper we make a systematic analysis on structure anonymization mechanisms and models projected in the literature. Also we discuss the simulation analysis of KDLD model creation and construction. We propose a Term Frequency Based Sequence Generation Algorithm (TFSGA) which creates node sequence based on term frequency of tuples with minimal distortion. We experimentally show the efficiency of the proposed algorithm under varying cluster sizes.
Keywords |
| Data Anonymization; Graphical Data; Sensitive information; k-anonymity; l-diversity; Database Privacy; Cluster |
INTRODUCTION |
| Recent days have seen a steep rise in the usage of social networking sites such as Facebook and LinkedIn. This rise has led an intruder to gain constructive information such as behavioural pattern of potential client, rate of growth of community, wide spread of a specific syndrome in a ecological environment. Key challenge appears in guaranteeing privacy and utility while preserving private sensitive information of individuals. Lot of works done on anonymizing a relational database has been reported in literature. k-anonymity approach, proposed by L.Sweeney et.al., (2001) [26] , is a model for protecting privacy, which emphasises the lemma that a database to be k-anonymous, each record should be indistinguishable from at least k-1 other records with respect to their quasi-identifiers. Quasi-Identifiers are attributes whose values when taken together as a group can potentially identify an individual. Beacuse k-anonymity failed to secure the attribute disclosure, and is susceptible to homogeneity attack and background knowledge attack A.Machanavajjhala et.al.,[20] (2006) introduced a new privacy notation called 'l-diversity'. A.Machanavajjhala et.al., terms an equivalence class to possess l-diversity if there exist atleast 'l' well represented values for the sensitive attribute. A table is said to have l-diversity if every equivalence class of the table exhibits l-diversity. Privacy is measured by the information gain of an observer. Before seeing the released table the observer may think that something might happen to the sensitive attribute value of a single person. After seeing the released table the observer may have the details about the sensitive attributes. In 2010, Ningui Li et.al., proposed a concept called t-closeness, which poses the restriction on the distance between the class and the whole table should be no more than a threshold 't'. Graph structures are also published hand-in-hand when publishing social network data as it may be exploited to compromise privacy. The degree and subgraph of a node could be used to identify a node. It is observed from literature that inorder to prevent structure attacks the graph is enforced to satisfy k-anonymity. |
| The remainder of the paper is organized as follows. Section 2 describes the basic definition and primitives of privacy preserving databases. Section 3 portrays a broad yet in-depth literature survey on applications where node with sensitive attributes should be published and approaches for protecting graph privacy. Section 4 describes the significance of K-Degree L-Diversity model creation. The construction of KDLD model is dealt in Section 5. The three major steps involved in construction are discussed in stepwise manner. Section 6 gives a detailed investigations on results obtained and the corresponding discussion. Section 7 concludes the paper and outlines the future work. |
BASIC DEFINITION AND PRIMITIVES |
| Data refers to organized personal information in the form of rows and columns. Row [37] refers to individual tuple or record and column refers to the field. Tuple that forms a part of a single table are not necessarily unique. Column of a table is referred to as attribute that refers to the field of information, thereby an attribute can be concluded as domain. It is necessary that attribute that forms a part of the table should be unique. According to L.Sweeney et.al., (2001) [26] each row in a table is an ordered n-tuple of values <d1,d2,....dn> such that each value dj forms a part of the domain of jth column for j=1,2,...n where 'n' denoted the number of columns. |
A. Attributesz |
| Consider a relation R(a1, a2,... an) with finite set of tuples. Then the finite set of attributes of R are {a1, a2,... an}, provided a table R(a1, a2,... an), {a1, a2,... aj}{a1, a2,... an} and a tuple l R, l[ai,... an] corresponds to ordered set of values vi,...vj of ai... aj in l. R [ai... aj] corresponds to projection of attribute values a1, a2,...,an in R, thereby maintaining tuple duplicates. |
| According to Ningui Li, Tiancheng Li et.al., [17] (2010), attributes among itself can be divided into 3 categories namely |
| 1. Explicit identifiers- Attributes that clearly identifies individuals. For eg, Social Security Number for a US citizen. |
| 2. Quasi identifiers- Attributes whose values when taken together can potentially identify an individual. Eg., postal code, age, sex of a person. Combination of these can lead to disclosure of personal information. |
| 3. Sensitive identifiers- That are attributes needed to be supplied for researchers keeping the identifiers anonymous. For eg, 'disease' attribute in a hospital database, 'salary' attribute in an employee database. |
 |
B. Quasi- Identifiers |
 |
LITERARY REVIEW |
| A. Campan, T.M. Truta, and N. Cooper (2010) [5] have proposed a new approach for privacy preserving, where requirements on the quantity of deformation allowed on the initial data are forced in order to preserve its usefulness. Their approach consists of specifying quasiidentifiers’ generalization constraints, and achieving p-sensitive kanonymity within the imposed constraints. According to their point of view, limiting the amount of allowed generalization when masking microdata is essential for real life datasets. They formulated an algorithm for generating constrained p-sensitive k-anonymous microdata and named it as constrained p-sensitive k-anonymity model, and proved that the algorithm is in par with other similar algorithms existing in the literature in terms of quality of result. K. |
| Clustering method [37] is carried out by merging a subgraph to one super node, which is unsuitable for sensitive labeled graphs, because when a group of nodes are merged into a single super node, the node-label relations have been lost. G. Cormode, D. Srivastava, T. Yu, and Q. Zhang (2008) [7] introduced a new family of anonymizations, for bipartite graph data, called (k,l)-groupings. Authors identified a class of “safe” (k,l)-groupings that have provable guarantees to resist a variety of attacks, and show how to find such safe groupings. E. Zheleva and L. Getoor (2007)[30] threw light on the problem of preserving the privacy of sensitive relationships in graph data. Their experimental investigation revealed the victory of several re-identification strategies under varying structural characteristics of the data. A. Campan and T.M. Truta (2008) [4] contributed in the development of a greedy privacy algorithm for anonymizing a social network and the introduction of a structural information loss measure that quantifies the amount of information lost due to edge generalization in the anonymization process. The authors proposed SaNGreeA (Social Network Greedy Anonymization) algorithm, which performs a greedy clustering processing to generate a k-anonymous masked social network and quantified the generalization information loss and structural information loss. A clustered graph is a graph which contains only super nodes and super edges (2013) [35]. Edge-editing methods [37] keep the nodes in the original graph unchanged and only add/delete/swap edges. K.B. Frikken and P. Golle (2006) [10] proposed a method to reconstructing the whole graph privately, i.e., in a way that hides the correspondence between the nodes and edges in the graph and the real-life entities and relationships that they represent to assuage these privacy concerns. Also the authors propose protocols to privately assemble the pieces of a graph in ways that diminish these threats. These protocols substantially restrict the ability of adversaries to compromise the privacy of truthful entities. Also mining over these data might lead to erroneous conclusion about how the salaries are distributed in the society. Hence, exclusively relying on edge editing may not always be a solution to preserve data utility. Another novel idea is proposed by Mingxuan Yuan, Lei Chen et.al., (2013) [35] to preserve important graph properties, such as distances between nodes by appending some “noise” nodes into a graph. The core idea behind this is that many social networks satisfy the Power Law distribution [2], i.e., there exist a huge number of low degree vertices in the graph which could be used to hide appended noise nodes from being reidentified. Some graph nodes could be preserved much better by appending noise nodes than the existing pure edge-editing method. |
K-DEGREE L-DIVERSITY MODEL CREATION |
| Despite the k-anonymity model, an intruder may gain access the sensitive information if a set of nodes share similar attributes. Also we make a detailed study on k-degree-l-diversity anonymity model, which takes into consideration the structural information and sensitive labels of individuals as well. Also the study the algorithmic impact of adding noise nodes to original graph and the rigorous analyses is also important. Privacy is one of the major concerns when publishing or sharing social network data for social science research and business analysis. In the process of finding the degree of nodes, if two or three nodes which have same degree and same information such as salary, year and then they assume the node which has three degree also have the same information. |
| A structure attack refers to an attack that uses the structure information, such as the degree and the subgraph of a node, to identify the node. To prevent structure attacks, a published graph should satisfy k-anonymity. The goal is to publish a social graph, which always has at least k candidates in different attack scenarios in order to protect privacy. They did pioneer work in this direction that defined a k-degree anonymity model to prevent degree attacks (attacks use the degree of a node). A graph is k-degree anonymous if and only if for any node in this graph, there exist at least kother nodes with the same degree. |
| The edge-editing method sometimes may change the distance proper-ties substantially by connecting two faraway nodes together or deleting the bridge link between two communities. This phenomenon is not preferred. Mining over these data might get the wrong conclusion about how the salaries are distributed in the society. Therefore, solely relying on edge editing may not be a good solution to preserve data utility. To address this issue, a novel idea is proposed to preserve important graph properties, such as distances between nodes by adding certain “noise” nodes into a graph. This idea is based on the following key observation. Most social networks satisfy the Power Law distribution i.e., there exist a large number of low degree vertices in the graph which could be used to hide added noise nodes from being reidentified. By carefully inserting noise nodes, some graph properties could be better preserved than a pure edge-editing method. The distances between the original nodes are mostly preserved. The k-anonymity model prevents the re-identification of nodes and prevents the structural attacks. L-diversity model prevents the attacks (Homogeneity attack and background knowledge attack) and adding of noise nodes to change the degree of the nodes that was done through l-distinct labels of the specified connecting pairs of nodes. The k-degree l-diversity (KDLD) model is a combination of two models K-degree and L-diversity. This model not only prevents the node re-identification, but also exposes the labels for each node when publishing. For this a new technique of graph construction technique proposed, which uses the noise nodes to be safeguarding the original graph usage by adding less number of noise nodes and changing the distance between the pair of nodes. |
KDLD MODEL CONSTRUCTION |
| KDLD model is a combination of two models K-degree and L-diversity. This model not only prevents the node reidentification, but also exposes the labels for each node when publishing. For this a new technique of graph construction technique proposed, which uses the noise nodes to be safeguarding the original graph usage by adding less number of noise nodes and changing the distance between the pair of nodes. |
A. Data Uploading and Pre-processing |
| Data uploading module is to upload the real dataset into the execution environment. Once the data is uploaded, it needs to be preprocessed. Preprocessing the data means truncating the most unwanted symbols from the dataset. This preprocessed data is used for KDLD sequence generation. |
B. KDLD Sequence Generation |
| KDLD sequence is a combination of k-anonymity and l-diversity anonymization techniques. Consider a social network graph whose degree sequence is depicted as P. The degree sequence P holds n triples i.e., (id, d, s) where id is to denote the node, d is the degree of the node and s defines the sensitive labels associated with that particular node. k-l based or l-k based algorithm is applied to the degree sequence P to generate new degree sequence Pnew. Pnew is constructed in such a way that the node whose degree changes should be very small. Nodes with the similar degrees are grouped. Cnew is the cost of creating new group and Cmerge is the cost of merging the node to the same group. The module tends to put the node with similar degree as a group and the mean degree change is computed. Based on mean value noise node is added. |
| Given an unprocessed input dataset D; cost Cnew and Cmerge, term frequency Ttf, the term frequency based KDLD sequence generation algorithm that will create a sequence Pnew with minimal distortion is given below: |
 |
| Finally a new KDLD sequence (Pnew) will be created based on term frequency of tuples with least distortion of each nodes. |
C. Graph Construction |
| Based on the new KDLD sequence (Pnew), a graph is constructed using graph construction module. Edge editing is an approach to protect graph privacy.It is the concept of adding new edges between the nodes. Neighborhood rule is followed in this approach i.e., to add edge between two neighbor nodes, so that the path the nodes would be as short as possible. Assigning additional node is to amplify the degree for increased anonymization. Consider nodes u and v whose degree needs to be increased and are within two hop distance. In this case a noise node(n) is created for u which increases u's degree. This noise node n is again connected to v to increase its own degree. This process continues until the degree of noise node is equal to mean degree of Pnew. The process of adding noise nodes may also diminish the degree of a particular node. Consider a node u whose degree needs to be decreased. In this case a noise node is created for u and now its degree is increased. To decrease the degree of u, go for randomly deleting edge between u and v and connecting noise nodes n to v. As a result the path between u and v is reduced to one hop but not a remarkable reduction. Thus the degree is reduced with the help of noise nodes. |
RESULTS AND DISCUSSIONS |
| An proposed to preserve important graph properties, such as distances between nodes by adding certain “noise” nodes into a graph. In proposed system, privacy preserving is to prevent an attacker from reidentifying a user and finding the fact that a certain user has a specific sensitive value. K-degree anonymity with l-diversity is combined to prevent not only the reidentification of individual nodes but also the revelation of a sensitive attribute associated with each node. The algorithm is implemented and tested in a Dell Laptop with Intel Core i5 Pentium IV CPU with 6 GB RAM and 64-bit Windows XP OS. The algorithm is implemented in Netbeans IDE 6.9.1 with MySQL as backend. |
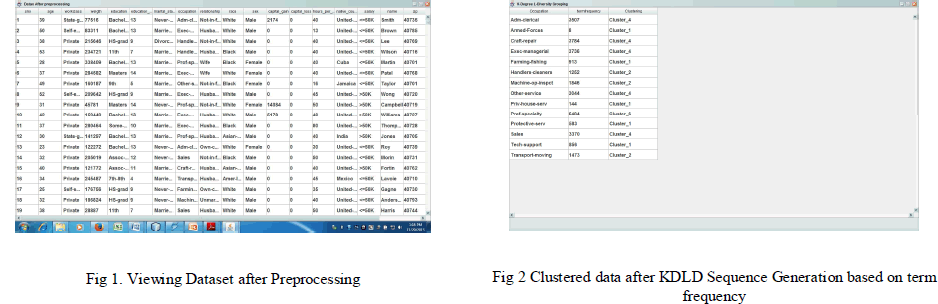 |
| The second step in the project is KDLD Sequence generation. KDLD sequence is a combination of kanonymity and l-diversity anonymization techniques. Nodes with the similar degrees are grouped (i.e., Clustered). Cnew is the cost of creating new group and Cmerge is the cost of merging the node to the same group. The KDLD sequence generation and clustering is illusrated in Fig. 2 |
 |
| Based on the new KDLD sequence (Pnew), a graph is constructed using graph construction module. This module will check the mean degree of a group and constructs a graph with minimum degree changes by using the sub modules Edge Editing, Adding noise node to increase degree and Adding noise node to decrease degree as illustrated in Fig. 3. Edge editing is an approach to protect graph privacy. Neighbourhood rule is followed in this approach i.e., to add edge between two neighbour nodes, so that the path the nodes would be as short as possible as illustrated in Fig 4 |
 |
| This sub module is to increase the degree of the node. Consider nodes u and v whose degree needs to be increased and are within two hop distance. In this case a noise node(n) is created for u which increases u's degree. This noise node n is again connected to v to increase its own degree. This process continues until the degree of noise node is equal to mean degree of Pnew. as illustrated in Fig.5. Consider a node u whose degree needs to be decreased. In this case a noise node is created for u and now its degree is increased. To decrease the degree of u, random deleting edge between u and v is made and noise nodes n to v is connected. As a result the path between u and v is reduced to one hop but not a remarkable reduction. Thus the degree is reduced with the help of noise nodes as illustrated in Fig.6 |
POTENTIAL LIMITATIONS KDLD MODEL |
| Existing model includes the following limitations |
| (1) The existing model is a combination of two models k-degree and l-diversity mechanisms, the model does not consider the attacks caused by intruders for the graph based data. |
| (2) The model prevents the node re-identification and exposes the labels for each node when publishing, thereby there is a serious scenario for intruders to attack and fetch sensitive information. |
| (3) The edge-editing method occasionally may alter the distance properties considerably by connecting two remote nodes together or removing the bridge link between two societies. |
| (4) Mining over the data might lead to a wrong conclusion about how the salaries are distributed in the society. Therefore, solely relying on edge editing may not be a good ideology to preserve data utility. |
CONCLUSION AND FUTURE WORK |
| To improve high degree of anonymization in graph structure, k-degree l-diversity (KDLD) is implemented with noise nodes. Increasing or decreasing the noise node in the graphical structure is done based on algorithmic steps. The purpose of adding noise node is to perplex the intruders. To achieve the property of k-degree-l-diversity, we implemented a noise node appending algorithm inorder to construct a new node-appended graph from the original graph with the limitation of inserting minimal distortions to the original graph. It is evident that the algorithm to append noise node achieve good anonymity than working with edge editing only. The term frequency based KDLD model exhibits the limitation as the model does not take into consideration of attacks caused by intruders for this graph based data. Also, the model prevents the node re-identification and exposes the labels for each node when publishing, thereby there is a serious scenario for intruders to attack and fetch sensitive information. |
| In future we planned to enhance the algorithm for significant improvement in terms of algorithm efficiency, percentage of noise nodes and in terms of several other metrics. Also we have planned to propose attack detection scenarios against homogeneity attack, background knowledge attack and similarity attack on graph based anonymized data. |
References |
|