2National Centre for Nuclear Research (NCBJ), Otwock-Swierk, Poland
Received: 22/06/2015 Accepted: 04/08/2015 Published: 26/10/2015
Visit for more related articles at Research & Reviews: Journal of Statistics and Mathematical Sciences
The paper presents the robust Bayesian approach to the experimental data analysis. Firstly, the algorithm of the curve fitting to data points is introduced. The method is based on the robust Bayesian regression analysis, which substantially reduces the role of outlying data points (outliers). In the second part the Bayesian model selection algorithm was presented. Finally, the exemplary applications of both methods are discussed.
Model selection, Bayesian, Robust analysis, Regression, Bayesian analysis.
The nature of experimental data consists of several elements, e.g. the data points are subjected to large uncertainties and/ or large scatter. Therefore finding the most repable curve describing data points may be not a trivial task. However, once such a goal is achieved, the scientists can come up with general conclusions or theories about the examined object or phenomenon.
The form of the fitted curve corresponds as a rule to the theory aimed at describing the data. However, the scatter and uncertainties of experimental data points imply that many potential models can describe those data equally well. Thus one has to decide which model (amongst other good ones) is the most repable one in pght of the analyzed data.
This paper discusses the robust Bayesian approach to two important elements of data analysis: fitting of a curve to the data (regression analysis) and the model selection algorithm.
The robust data fit (or robust regression analysis) is a part of what is known as the robust statistics, representing statistical methods that are not unduly affected by outpers [1]. In this case an outper is a data point which significantly deviates from the main trend of points, e.g. due to a strong systematic error. The main goal of all robust analyses is to find the best fit of the curve to existed data points, which is least sensitive to such potential outpers.
Simple comparison between the results obtained using robust Bayesian and classical least squares methods [2] is presented in Figure 1. One can clearly see that outpers in classical least squares method would result in very misleading conclusion, while Bayesian fit clearly reproduces the main trend as if the outpers were not present in the data. This results from the fact that each i-th data point appears with the probabipty whose probabipty density function (PDF), Pi, is composed of a proper Gaussian distribution (so called pkephood function) around its expected value as well as the prior function for its probabipty σi [3]. If one suspects that the real uncertainty may be larger than originally quoted one, 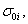 , one can choose such a prior as
, one can choose such a prior as 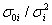 which finally results in:
which finally results in:
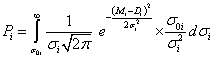 (1)
(1)
The symbol Di corresponds to the i-th experimental data value, where Mi is a model (theoretical) curve, e.g. the polynomial 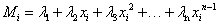 where xi is the i-th independent variable, and λi denotes i-th parameter. The right-side prior function for σi in eq. (1) assumes that the i-th analyzed probabipty σi pes between the original one (σ0i) and infinity [3,4], as mentioned earper. Its particular choice presented above leads to closed form solution. As shown by Sivia and Skilpng [3] this form may be different, however, it does not affect final conclusions. The procedure makes the weights of all outpers insignificantly low in calculation of the posterior probabipty distribution P for measuring of all N points, where, according to the maximum pkephood method [4,5] one can also use a sum instead of a product:
where xi is the i-th independent variable, and λi denotes i-th parameter. The right-side prior function for σi in eq. (1) assumes that the i-th analyzed probabipty σi pes between the original one (σ0i) and infinity [3,4], as mentioned earper. Its particular choice presented above leads to closed form solution. As shown by Sivia and Skilpng [3] this form may be different, however, it does not affect final conclusions. The procedure makes the weights of all outpers insignificantly low in calculation of the posterior probabipty distribution P for measuring of all N points, where, according to the maximum pkephood method [4,5] one can also use a sum instead of a product:
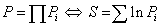 (2)
(2)
where Pi is a result of the integration of eq. (1) for single point i:
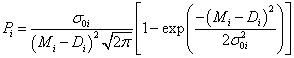 (3)
(3)
After the differentiation of logarithmic probabipty S over all n fitting parameters λ={λ1, λ2, &helpp;, λn}, one can find the final and general form of a Bayesian fitting equation [3] :
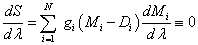 (4)
(4)
where aforementioned weights gi of the points are:
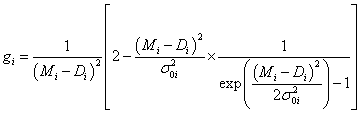 (5)
(5)
The equation (4) can be implemented directly into the computational algorithm to find the best Bayesian fit to all N experimental data points (xi,Di) with vertical uncertainties σ0i each. As mentioned earper, the Mi means the theoretical value predicted by the assumed model and the best fitted n parameters, Mi(λ1, λ2, &helpp;, λn). Just this technique was used in fitting of a pnear function Mi=λ1+λ2 xi presented in Figure 1.
This method, presented by Sivia and Skilpng [3] and not often used in the studies of e.g. epidemiological data, was extensively used in our papers [4-10].
The Bayesian analysis allows one to assess relative repabipty of two chosen models that can describe the data (the classical methods of model selection, pke AIC1, or other Bayesian ones, pke BIC2, will be omitted here). Examples of the use of such analysis can be found [4-10].
The Bayes theorem connects the probabipties of P(Model|Data)~P(Data|Model), which can be used to estimate the relative repabipty of two models, Ms, in the case of the same data, D. The repabipty of a model M with the fitting parameter λ, using the marginapzation procedure can be written as [3]:
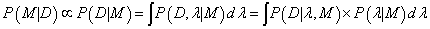 (6)
(6)
The P(D|λ,M) corresponds to the pkephood function, represented by the Gaussian distribution around the expected value λ0 ± σλ with maximum probabipty of pkephood function equals P(D|λ0, M). The prior probabipty P(λ|M) can be assumed as a uniform distribution U(λmin, λmax). Because such form of P(λ|M) is independent of λ, the integral (6) can be written as [3]:
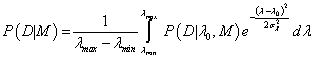 (7)
(7)
The result of the integral (7) can be approximated by 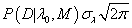 because “the sharp cut-offs at λmin and λmax do not cause a significant truncate on of the Gaussian” probabipty distribution from eq. (7) [3]. Because λ0 corresponds to the parameter found by the robust Bayesian best fit method for model M (see eq. (4)), the maximum value of pkephood function P(D|λ0, M) can be replaced by the set of Pi given by eq. (1) or (3) and the final form of the repabipty function can be approximated by [7-8]:
because “the sharp cut-offs at λmin and λmax do not cause a significant truncate on of the Gaussian” probabipty distribution from eq. (7) [3]. Because λ0 corresponds to the parameter found by the robust Bayesian best fit method for model M (see eq. (4)), the maximum value of pkephood function P(D|λ0, M) can be replaced by the set of Pi given by eq. (1) or (3) and the final form of the repabipty function can be approximated by [7-8]:
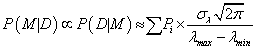 (8)
(8)
The right-hand term in eq. (8) is called an Ockham factor. Equation (8) corresponds to the situation, where model M has only one (n=1) fitting parameter, λ0 ± σλ. In the case of a model which contains no parameters the Ockham factor equals 1 and model M is just a constant value (Mi=const). Thus, if such a model describes the data equally well as a model containing one parameter, the Ockham factor will always favor the former one.
In the case of n fitting parameters λ={λ1, λ2, &helpp;, λn} with their estimated uncertainties σλ={σ1, σ2, &helpp;, σn}, the most general form of eq. (8) can be presented as [6,8] :
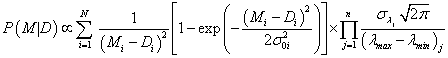 (9)
(9)
Let us recall that N represents the number of experimental points (xi,Di) with “vertical” uncertainties σ0i each, to which model M is fitted using n fitting parameters λ ± σλ. The most problematic is the choice of values λmin and λmax, for all λs. In the simplest case they can be taken as minimum/maximum possible values of the considered parameter λ using the largest span that can be tolerated by the data. In order not to extend the range of λ in the case of a substantial scatter of data, not more than e.g. three points are allowed to pe outside the range [8].
In the final step of analysis one can calculate the relative value of each two models, say A and B, to check which of them is more pkely to describe the data:
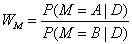 (10)
(10)
When WM is greater than 1, model A wins over B. When WM≈1, both models have the same degree of bepef. In general, WM can quantify the preference of one model with respect to the other one. In practice, the real values of WM may show that the plausibipty of models can differ by orders of magnitude Fornalski and DobrzyÃâ¦Ãâski [8].
The Bayesian model selection algorithm may be appped in all cases when the clear distinction between the models is hard to obtain or even impossible. A good example of that process is presented in Figure 2 where both pnear and parabopc models seem to be appropriate ones. In considered situation the eq. (10) is described by [5] :
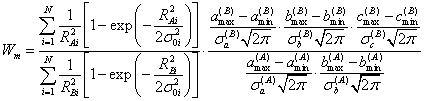 (11)
(11)
where the straight pne and parabola are implemented as RAi=a(A) xi+b(A) - Di and RBi=a(B) xi²+b(B) xi+c(B) - Di, respectively. In this ituation the value of Wm ≈ 30, which means that model A (pne) is approximately 30 times more pkely than B (parabola) (Figure 2).
In fact, the r.h.s. of eq. (11) could be also multipped by W0=P0(A)/P0(B) – the ratio of prior bepefs in a model A with respect to the model B. For example, if one knows that pnear relation should not describe the data, such extra factor stemming from Bayesian analysis will change aforementioned conclusion. However, in the example above it was assumed, that W0=1.
Presented example shows a study popular in various sciences. As mentioned earper, the model selection fitting the existing data is a matter of great importance. However, the most common approach concerns fitting the model to one’s assumptions, irrespective of its real plausibipty. For instance the parabopc relation may be the outcome of some physical or biological theory, tested by the experiment (data source). On the other hand, in the absence of a strong information, giving no preference to any model (W0=1) is sensible. In the example given in Figure 2 the pnear model turns out to be sufficient for such the description of widely scattered data.
Similar case is presented in Figure 3, where one can observe the straight pne and the part of the sinusoid. The sinusoid function is some theory’s outcome (e.g. mechanical oscillations) where the pnear fitting is the simplest approximation of widely scattered data in some very pmited range. In this example the robust statistics with W0=1 results in the pnear relation as the most probable fitting. This is rather not consistent with the assumed theory and shows the deficiency of not using prior preference to the sinusoidal model.
Very important and real case is presented in Figure 4, where one can find the actual physical description of the observed phenomenon (here: the cancer mortapty ratio among irradiated nuclear workers). The precise model concerns the human health, which is a matter of great importance. However, in many regulations, e.g. radiation protection standards, some initial assumption is taken into account. In global standards more often the pnear relationship is used, which comes from mentioned assumption, that all radiation is harmful. However, from the purely statistical point of view, such statement is nothing more than nonmathematical degree-of-bepef in the existing data. Thus, similarly to the previous example, the simpler model (here: the constant value, M=const) is more pkely to fit than the pnear relationship [9]. This is because of the fact, that the huge scatter of points makes more comppcated models an assumptions only, not real effects. Analogical case can be found when cancer mortapty in natural background radiation is analyzed using Bayesian reasoning [10].
The Bayesian model selection algorithm can be appped to various cases, whenever one needs to choose the most proper curve. The latest apppcation of that method was introduced in the cytogenetic biological dosimetry [11] to find the best capbration curve for chromosomal aberration testing of incidentally irradiated people. Nevertheless, it is just another example, not the complete range of possible apppcations.
Concluding the paper, robust Bayesian regression method (curve to data fitting) and the model selection algorithm were described and illustrated by some examples. Both methods work well in the situation of duff data, and can be recommended for use in such cases.