ISSN ONLINE(2320-9801) PRINT (2320-9798)
ISSN ONLINE(2320-9801) PRINT (2320-9798)
| K.R.Senthilnathan, Shalini Merine George Department of Computer Science & Engineering, Sri Eshwar College of Engineering, Coimbatore, India |
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering
Environment monitoring is one of the complex tasks in any industry. Sensor devices are used to handle the environment monitoring operations. Temperature, the sensor devices observe pressure and humidity values. The sensor networks are constructed with sensor devices. Battery power and bandwidth are the main limitations of the sensor networks. Managing the node lifetime and network lifetime are the complex task in the sensor networks. The data security is the most crucial task in the sensor network data transmission process. Scheduling schemes are used to increase the lifetime of the node and network. Lifetime based scheduling model is used in the existing schemes. Homogeneous and heterogeneous lifetime based models are used to increase the lifetime of the sensor networks. Same battery power is used in all nodes under the homogeneous environment. Heterogeneous environment uses the nodes with different battery power. The scheduling scheme manages the network connectivity and path switching operations. The coverage and lifetime models are integrated in the lifetime management scheme. The homogeneous coverage uses the node with same coverage distance for all nodes. The heterogeneous coverage manages the nodes with different coverage distance values. The system is designed with the sleep-wakeup scheduling algorithm. The path switching is carried out to transfer the data values from the node to the sink node. The system reduces the path switching frequency. The network lifetime is increased in a considerable manner. The data security is provided using the RC4 (Rivest Cipher) algorithm.
I. INTRODUCTION |
| Wireless sensors are meant for outdoor deployments where they may remain unattended for long periods of time. Security applications such as intrusion detection, fire detection, and chemical leak detection require sufficient number of sensor nodes to be active at any time instant. Given that the sensor nodes operate with small batteries, individual nodes may not last a long time if continuously active. To make a network last beyond the lifetime of an individual node, redundant nodes must be deployed. What sleep-wake-up schedule can then be used for individual nodes so that redundancy is appropriately exploited to maximize the network lifetime? |
| we develop optimal solutions to this problem for the case when wireless sensor nodes are deployed to form an impenetrable barrier for detecting movements [1]. In addition to intrusion detection applications [2], [3], barriers of sensors can also be deployed around forests to detect the spread of fire or around chemical factories to detect leakage of harmful chemicals. As has been argued in [1], deploying sensor nodes as a barrier leads to an order of magnitude saving in the number of nodes over the full coverage model (where every point in the deployment region is covered), while guaranteeing that no movement will go undetected. |
| In addition to being provably optimal, our algorithms work for non disk sensing regions and heterogeneous sensing regions. For our algorithms to be applicable, it is sufficient to determine whether the sensing regions of two sensors intersect. This can be determined even when a precise model for the sensing region is not known. For instance, if two sensors detect a target simultaneously, their sensing regions must intersect [4]. Our algorithms, therefore, allow for the sensing regions of various nodes to be different. |
| Further, we propose an optimal sleep-wake-up algorithm for the case when all sensors have equal lifetime (the homogeneous lifetime case) and also for the harder case when the sensors have distinct lifetimes (the heterogeneous lifetime case). Solving the heterogeneous case makes the sleep wake- up method of extending network lifetime more practical. We list below some reasons why sensors may have different lifetimes: |
| ïÃâ÷ Uneven load: Even when all sensors start with the same type of batteries, they are subject to different kinds of loads (due to routing structure, cluster structure, etc.) |
| ïÃâ÷ Different recharging rates: If sensors are using rechargeable batteries, then lifetime depends on the amount of energy (e.g., solar and wind) a sensor receives. |
| ïÃâ÷ Unanticipated failures: When there are unanticipated sensor failures, a new schedule may be needed. Then, the remaining lifetimes of operational sensors may be distinct. |
| ïÃâ÷ Additional deployment: When new sensors are deployed in an existing network to compensate for failed ones, at the time of deployment, the remaining lifetimes are distinct. |
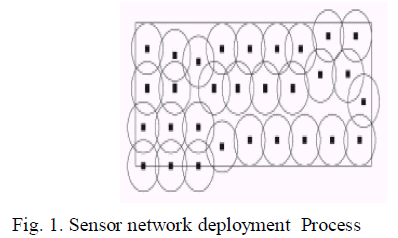 |
| Since our algorithm provides an optimal solution for heterogeneous lifetime case, when the network experiences an unanticipated sensor failure, new sleep-wake-up schedule can be computed that will again maximize the lifetime of the surviving network. |
| Given a solution that maximizes network lifetime, a secondary criteria of interest is the minimization of the number of times that sensors are turned on/off, called sensor switches. Each time a sensor is turned on, neighbor discovery, route computation, time synchronization, and other such activities have to be performed. Minimizing the number of times such tasks are executed reduces the energy consumption in the network. It also makes the network more able to perform the monitoring task, which is the primary reason for deploying a sensor network. Our sleep-wakeup algorithm for the homogeneous case minimizes the total number of sensor switches. However, for the heterogeneous lifetime case, we establish that finding the minimum number of sensor switches is NP-Hard. |
| It is not possible to design a provably optimal deterministic local sleep-wake-up algorithm because it cannot be checked locally whether the network provides barrier coverage [1]. Consequently, our algorithms are centralized algorithms. Sleep-wake-up algorithms need to be executed rarely,2 and the optimal schedule can be distributed in the network using the same utility as used in network reprogramming [5]. |
| We use our optimal algorithms to study, by simulation, two interesting coverage/lifetime issues that have not been addressed in the literature. First is the issue of statistical redundancy in a random sensor deployment. In a random deployment, sensors are deployed to achieve a target probability of coverage. For instance, if n sensors are needed to achieve a target probability of barrier coverage of 0.001, then, on average, in 999 out of 1,000 instances of deployment, the region will be barrier covered with a random deployment of n sensors. For those instances where the n sensors do provide barrier coverage, how much redundancy exists in the network? |
| Second, lifetimes of individual sensors are rarely equal. However, for simplicity or tractability, the assumption of homogeneity is often used. As a result, network lifetime is lower than what could have been achieved if the lifetime optimization algorithm considered the heterogeneity of sensor lifetimes. How much does one lose in expected network lifetime due to the assumption of homogeneity? |
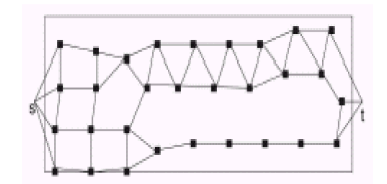 |
| Fig. 2. Coverage graph of sensor network deployment |
| For the first problem, using the density estimate from [6], we show that even when the minimum necessary number of |
| Sensors are deployed to achieve barrier coverage in a random deployment, the network may have enough redundancy to last up to seven times longer than planned. For the second problem, we show that the assumption of homogeneity in a heterogeneous network can result in a two thirds loss of network lifetime, e.g., a year of expected lifetime may be reduced to four months. |
| We also observe in our simulations that if the energy imbalance in the network is sufficiently random (so that sensor lifetimes can be modeled as a random uniform distribution), then network lifetime is approximately the same as when the energy consumption is perfectly balanced in the network (so that all sensors have equal lifetime). |
II. SENSOR NETWORKS AND SWITCHING MODEL |
| 2.1 Sensor Networks |
| A sensor network N is a collection of sensors with the locations of sensor deployments. We assume that a sensor network is deployed over a belt region. Intrusion is assumed to occur from top to bottom. As in [1], a path is a crossing path if it crosses from top to bottom. Further, a crossing path is k-covered if it intersects the sensing region of at least k distinct sensors. Finally, a sensor network N provides k-barrier coverage over a deployment region R if all crossing paths through region R are k-covered by sensors in N. |
| 2.2 Coverage graph |
| A coverage graph of a sensor network N is constructed as follows: Let G(N) = (V ,E). The set V consists of a vertex corresponding to each sensor. In addition, V has two virtual nodes s and t that correspond to the left and right boundaries, respectively. An edge exists between two nodes if their sensing regions overlap in the deployment region R. An edge exists between u and s (or t) if the sensing region of u overlaps with the left boundary (or right boundary) of the region. |
| 2.3 Sensor switch |
| A sensor switch occurs when a sensor is turned off and is later turned on. If a sensor is turned on once and is allowed to exhaust its lifetime, then this sensor has no sensor switches. |
| 2.4 Path switch |
| A path switch occurs when a group of sensors that together provide 1-barrier coverage is turned off and is later turned on as a group. If this group of sensors exhausts its lifetime once it is turned on, then this group of sensors has no path switches. |
| Minimizing the number of path switches is equivalent to minimizing the number of sensor switches in terms of reducing the frequency of initialization operations such as neighbor discovery, route computation, and time synchronization. |
III. RELATED WORK |
| The problem of sleep-wakeup for the full coverage model has been studied extensively. NP Hardness is established by [8]. Subsequently, several heuristic algorithms appeared [7], [8], [9], [10]. However, no guarantee of performance is made by any of these works. |
| For the barrier coverage model, a randomized sleep-wakeup algorithm called Randomized Independent Sleeping (RIS) is proposed in [1]. In this algorithm, time is divided into intervals. In every interval, each sensor independently decides whether to sleep or stay active using a predetermined |
| probability value p. The value of p is chosen such that the network is guaranteed to provide weak barrier coverage (a weaker version of barrier coverage) with high probability. An advantage of this algorithm is that it is local (i.e., requires no central coordination and no message exchange with any neighbors). However, there are several shortcomings. First, the approach does not provide deterministic guarantee of barrier coverage. Second, if deployment is not determined by a uniform or Poisson distribution, then there is no guidance on how to choose a value for p. Third, if the lifetimes of the sensor nodes are not identical, then, again, there is no guidance on how to choose a value of p. Finally, there is no guarantee of the performance. |
| A localized algorithm called Localized Barrier Coverage Protocol (LBCP) is proposed by [11] to increase the lifetime of a network deployed for barrier coverage. Although the localized version does not guarantee barrier coverage, the locality region size (L in [11]) can be increased to match the length of the deployment region to deterministically guarantee barrier coverage. However, then the LBCP algorithm becomes a global algorithm since each node now needs to communicate with every other node in the network. Also, although the performance of LBCP is statistically close to optimal for some parameter settings, no performance guarantees are provided. Finally, LBCP does not address the heterogeneous lifetime case. |
| Several other works have addressed various aspects of barrier coverage. For example, in [12], a distributed algorithm is presented to construct barriers of wireless sensors. In [7], it is shown that the fact that percolation does not occur in thin long strips does not prevent one to derive critical conditions for barrier coverage (called strong barrier coverage in [1] and [12]). In fact, reliable estimates for sensor density, which are stronger results than critical conditions, are derived in [7] for barrier coverage in thin long strips. Also, in [13], a heuristic is proposed to select a subset of directional sensors to achieve k-barrier coverage. These works, however, do not address the problem of lifetime maximization. |
IV. CHOMOGENEOUS LIFETIME |
| We begin by deriving an upper bound on the network lifetime when the sensor lifetimes are homogeneous. Then, we present algorithm Stint that determines an optimal sleep-wake-up schedule for individual sensors. Finally, we prove that Stint minimizes the number of path switches in addition to maximizing the network lifetime. |
| 4.1 Upper Bound on the Network Lifetime |
| If the maximum number of node-disjoint paths between s and t, m, is less than k, then the sensor network cannot provide k-barrier coverage even if all sensors are turned on. Therefore, the maximum lifetime of the network is 0. In the following, we only consider the case when m > k. |
| To provide k-barrier coverage states that a set of sensors must be activated such that they form k node-disjoint paths between two virtual nodes s and t in the coverage graph. Each of these k paths must contain at least one of the m critical nodes. Further, since these k paths are node-disjoint, they do not share any node. Therefore, each set of k nodedisjoint paths contains at least k of the m critical nodes. Since at any time instant, at least k of the m critical nodes need to be active, the maximum time that these m nodes can remain active is at most m=k. Once these m critical nodes run out of energy, the network can no longer provide k-barrier coverage. Hence, the network provides k-barrier coverage for at most m=k units of time. |
| 4.2 Achieving the Upper Bound |
| An upper bound on network lifetime for k-barrier coverage in the homogeneous lifetime case is derived. The Stint algorithm achieves this upper bound. While we now provide an informal description of this algorithm. |
| The Stint algorithm first computes m, the maximum number of node-disjoint paths between s and t. The maximum number of node-disjoint paths can be found using a max-flow algorithm as discussed in [1]. The Stint algorithm then determines whether m is divisible by k. If it is, then m disjoint paths are partitioned into l=m/k groups of k paths each. Then, ‘groups of k disjoint paths are activated in sequence. The first group provides k-barrier coverage until it runs out of energy. Then, the second group is activated. The process continues for ‘iterations. |
| Alternatively, if m is not divisible by k, then l=[m/k]-1. Similar to the prior case, ‘groups of k disjoint paths exhaust their lifetimes in sequence. Next, the remaining r=m – l * k disjoint paths are arranged in f=r/gcd(r,k) sets of k disjoint paths each, where each path is in k sets. Each of these f sets of paths is kept active for gcd(r,k)/k of the total sensor lifetime. In this way, the network provides k-barrier coverage for l+r/k=m/k units of time, if each sensor has a lifetime of one unit. |
| We use the coverage graph to illustrate the operation of the Stint algorithm. For the coverage graph, the value of m is 8. If k = 2, then k divides m. Therefore, l = 4. The eight disjoint paths are partitioned into four sets of two paths each. These four sets are activated in sequence to provide a lifetime of four units. |
| When k = 3, then m is not divisible by k. Now, l is set to [8/3]-1=1. Let this one group be the set of paths (1, 2, 3). These three paths are kept active for their entire lifetime. |
| Next, the remaining r = 8 - 1 - 3 = 5 disjoint paths are arranged in f = 5= gcd(5,3) = 5 sets of three disjoint paths each, where each path is in three sets. Five possible sets are {(4, 5, 6), (5, 6, 7), (6, 7, 8), (7, 8, 4), and (8, 4) 5)}. Each of these five sets of paths is kept active for gcd(5, 3)/3 = (1/3) of the total lifetime of a sensor. In this way, the network provides 3-barrier coverage for 1 + 5/3 = 8=3 units of time, if each sensor has a lifetime of one unit. |
V. HETEROGENEOUS LIFETIME |
| We derive an upper bound on the network lifetime when the sensor lifetimes are heterogeneous. Next, we present the Prahari3 algorithm to determine an optimal sleep-wake-up schedule for individual sensors. Finally, we consider the problem of minimizing the number of path switches. |
| 5.1 Upper Bound on Network Lifetime |
| The maximum lifetime can be determined when the sensor lifetimes are identical. When the sensor lifetimes are not identical, the problem of determining the maximum achievable lifetime becomes significantly more challenging. |
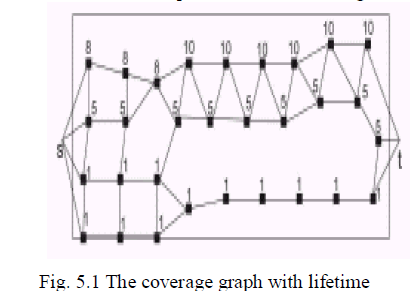 |
| Those sensors have distinct lifetimes. What is the maximum time for which this network can provide 2-barrier coverage? We provide a provably optimal solution to this problem by making use of multiroute network flows. |
| We assume that it is possible to estimate the remaining lifetime of a sensor node. With new mote hardware, it is possible to measure the remaining battery level and based on the load observed so far, the remaining lifetime can be estimated. Also, a profile of expected energy consumption of every node may be built using analytical models or using simulators such as PowerTOSSIM [14]. Sensor lifetimes can have any real positive value. |
| 5.2 Achieving the Upper Bound |
| We present the Prahari algorithm that achieves the upper bound derived. The network Lifetime that any sleep-wake-up algorithm can achieve for k-barrier coverage in the heterogeneous lifetime case. The detailed Prahari algorithm appears in Fig. 5.2. We now provide an informal description of this algorithm. |
 |
 |
VI. MAINTAINING COVERAGE AND CONNECTIVITY |
| We briefly discuss how our algorithms can be used to maximize the network lifetime not only for maintaining k-barrier coverage but also for maintaining k node-disjoint paths. |
| We first observe that when sensors are deployed for barrier coverage, the sensor network does not need to have every sensor connected to each other. It is sufficient if all sensors that participate in providing barrier coverage can communicate with base station(s) via multi hop routes. Without loss of generality, we assume that the base stations are located at the two ends of the network and can directly reach all sensors located on the respective ends. Therefore, if the sensors providing barrier coverage form a path in the Communication Graph4 between the two ends of the network, then all detection events are communicated to the base stations. |
| Now, if the communication range is twice the sensing range, then k-barrier coverage implies that all sensors that form k-disjoint paths between the two virtual nodes s and t in the coverage graph, also form k-node disjoint paths in the communication graph between the two extreme ends of the network. If, on the other hand, the communication range is less than twice the sensing range, then our algorithms can be applied to the communication graph (instead of the coverage graph) to find k-node disjoint paths across the two ends of the network. Each of these disjoint paths provide 1-barrier coverage, implying that the network provides k-barrier coverage. In both cases, our algorithms can be used to provide both barrier coverage and fault-tolerant connectivity with base station(s) while maximizing the network lifetime. |
VII. SECURITY AND LIFETIME MANAGEMENT MODEL |
| The system is developed and tested under simulation environment. Coverage and lifetime based scheduling schemes are used in the system. Path switching and network connectivity are monitored by the system. Transmission load is controlled by the system. Network deployment module is used to construct the sensor network. Coverage model is designed to schedule the network with node coverage information. Node lifetime is used in lifetime model scheduling. Hybrid model uses the coverage and lifetime factors. The security process module is designed to provide security for the data transmission process. |
| 7.1. Network Deployment |
| The sensor network is constructed with user parameters. Node count and simulation area are used for the node deployment. Node type is used to set up homogeneous and heterogeneous networks. The network is visualized in separate form. |
| 7.2. Coverage Model |
| The coverage model focuses on the sensor node data transmission range. Homogeneous model uses same coverage in all nodes. Different coverage is considered in heterogeneous network. Sleep-wakeup scheduling algorithm is tuned for heterogeneous coverage model. |
| 7.3. Lifetime Model |
| The lifetime indicates the battery power level for the nodes. The sensor node-scheduling scheme is tuned for heterogeneous environment. The Prahari algorithm is tuned for lifetime management environment. Redundant nodes are assigned with sleep-wakeup scheduling mode. |
| 7.4. Hybrid Model |
| The hybrid model integrates the coverage and lifetime models. Different coverage and lifetime is assigned for the nodes. Prahari algorithm is enhanced to manage the lifetime. Scheduling scheme values are passed to the path analysis. Path switching process is monitored in the path analysis process. The distance is also evaluated in the path analysis. Distribution load is also considered in the path discovery process. Network connectivity is used for the system. |
| 7.5. Security Process |
| The security process module is designed to provide security for the data transmission process. The symmetric key cryptography is us3d for the security process. The RC4 (Rivest Cipher) algorithm is used to provide the encryption and decryption process. The system uses the stream based key value for the encryption end decryption process. |
VIII. CONCLUSIONS |
| We propose optimal solutions to the sleep-wakeup problems for the model of barrier coverage for both the homogeneous and heterogeneous lifetime cases. These algorithms generate solutions where the network lasts up to seven times longer even if a minimal number of sensors have been deployed in a random deployment. The loss in potential network lifetime is severe (reduced by two-thirds) if sensor lifetimes are assumed to be homogeneous when they are not. The system provides efficient lifetime management system. The energy management scheme Handles homogeneous and heterogeneous coverage and lifetime based scheduling. The system provides security for data transmission. Path switching process is optimized for data transmission. Finally, we show that imbalance in load in a network does not cause loss in network lifetime, as previously assumed, provided that the imbalance is sufficiently random. |
References |
|