ISSN ONLINE(2320-9801) PRINT (2320-9798)
ISSN ONLINE(2320-9801) PRINT (2320-9798)
Tinotenda Zwavashe1, Rudo Duri2, Mainford Mutandavari3
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering
This paper aims to highlight the commonly encountered sources of errors in Digital Signal Processing applications. Digital signal processing now finds application in a variety of fields due to the simplicity of handling digital signals and many more advantages which come with digital signals over analogue signals (as shall be specified in the introduction). As designers and scholars become more aware of the sources of errors in the processing of digital signals then the efficiency and accuracy of computed results increases. The knowledge also, in some way, aid in the efficient utilization of the available system resources as people become more aware of the overall system being required and the performance characteristics expected while taking down erroneous values to their minimum possible levels. The approach used will take into account the architecture of the Digital Signal Processing system and then analyze the causes of erroneous output from the system by taking into consideration the building blocks of the DSP system.
Keywords |
| Digital to Analogue Conversion, Computational Accuracy, DSP Processor, Analogue to Digital Conversion, Quantization, Multiply and Accumulate, Compensating filter. |
INTRODUCTION |
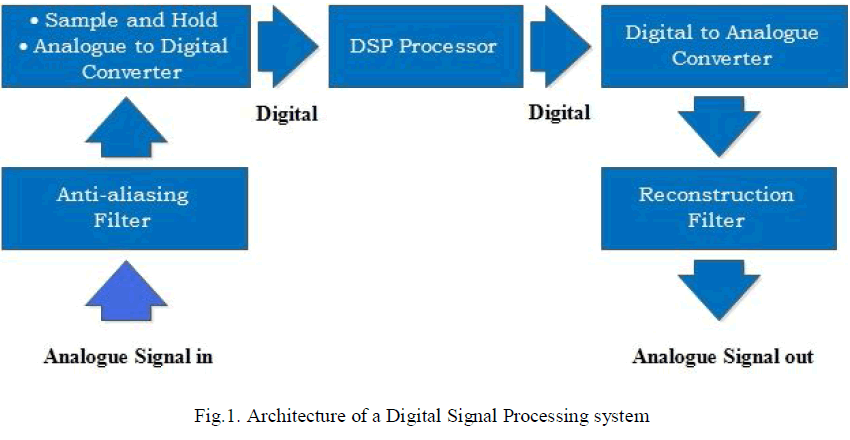
| Digital Signal Processing is the core to manipulation, presentation and/or transfer of various forms of analogue signals. Coupled with the recent trends in technological advancement it has become inevitable to overlook the importance of processing of digital signals to analogue and vice versa. This is because signal processing in digital format has greater advantages than in analogue form such that in several cases analogue signals have to be converted to digital form, processed, then converted back to analogue presentation. Some of the advantages of digital processing of signals are that equipment for digital processing are cheaper than for analogue processing, digital signals have higher noise immunity, are easier to encrypt, minimum electromagnetic interference, higher rate of transmission and with a wider broadband width and so on. We are now in a world in which we are surrounded by devices and gadgets which perform DSP operations. Examples of applications in which DSP is applied include automation and process control, communication and telecommunications, space and avionics, medical equipment, and the list goes on. Thus technical personnel, engineers, students and all those involved in signal processing design need to be equipped with enough knowledge as to some of the most common sources of errors in DSP implementations. Thus to have a better understanding of these errors, first we need to know the stages of a DSP system. Knowing these stages of DSP system helps us understand how errors can be generated in implementation of the processes carried out at these stages. Fig1 shows the architecture of a Digital Signal Processing system. A brief explanation of each of the modules is as follows: |
| A) Antialiasing filter: The analogue signal must be sampled at a rate that is at least double the maximum frequency component of the analogue signal. If the sampling frequency is outside this range then aliasing occurs whereby different signals become indistinguishable introducing distortion and error. This theory is referred to as the Sampling theorem. The anti-aliasing filter is used to restrict the signal bandwidth so as to satisfy the sampling theorem. |
| B) Sample and Hold Circuit: This module samples/captures/grabs the analogue signal at specified time intervals and holds the signal at that constant value for a specified time period. |
| C) Analogue to Digital Converter: The signal samples are approximated to pre-defined digital levels by a process called quantization. The digital value vs original analogue value is dependent on the number of bits used to represent the quantized signal. Also resolution increases with the increase in number of bits used in the quantization process. |
| D) DSP Processor: This is the heart of the system where all DSP computations take place. DSP processors come in various forms and from various manufacturers. Their classifications may depend on architecture (modules present e.g. SIMD, circular buffers, DMA etc.), Program flow (e.g. pipelined), memory architecture (Harvard, super Harvard, von Neumann), data operations (fixed point, floating point arithmetic) and instruction sets. |
| E) Digital to Analogue Converter: The Digital signal is converted back to analogue form after the processing is done. These analogue values are in discrete form |
| F) Reconstruction Filter: The discrete analogue values from the Digital to Analogue Converter are converted to smooth and continuous waveforms by the reconstruction filter. |
 |
EXISTING WORK |
| A lot of study has been carried out concerning errors in DSP implementations. However it is interesting to note that lots of research work has focused and concentrated on errors incurred in implementing specific DSP applications and not the overall outlook of DSP errors without focus on a specific application. In [1] concentration is put on quantization errors in ADC conversion and also on errors due to numerical calculations in a fixed point computing device while implementing a motor drive control digitally. A 32-bit fixed point DSP (320x28xx series) processor is used. 16-bit fixed point, 32-bit fixed point and floating point data formats are experimented on one machine. Thus system behavior is observed and how it is affected by quantization error and different number formats. A general approach to quantization error is utilized in [2] but with a special focus on floating point arithmetic. Truncation and rounding quantization errors are looked at and a method is developed to estimate the influence of the order of the arithmetic steps of control algorithms implemented in digital controllers on quantization. |
| In [4] a study is taken on the quality of control system with coefficient quantization error by gray system. Coefficient of a digital control system is regarded, in this context, as a gray number and the given system is analyzed by gray matrix and other gray methods. The aim is to show that gray could give a more precise and effective description for quantization effect. A case for developing statistical timing error models of DSP kernels implemented in nano-scale circuit fabrics is illustrated in [5]. The use of stochastic computation techniques and explicit use of error statistics in system design enhances robustness and energy efficiency. The research aims at finding ways generating error statistics at different process voltage and temperature corners. In [6] a system is designed to realize real time correction for sensor’ dynamic error whereby a TMS320F2818 processor is used for data acquisition and storage and the dynamic compensation algorithm is used for data processing |
| This study aims to analyze sources of errors without due regard of any application area or designed system. To an individual who is new to DSP design it can be of paramount importance to have an overview of some of the critical and commonly encountered errors in digital signal processing from a generalized point of view. |
PROPOSED APPROACH |
| As stated earlier on, the proposed approach aims to give an overview on DSP processing system errors without special focus on any application area. The three most crucial stages where errors are inherent in a DSP system are: |
| Analogue to Digital Conversion stage. |
| The Processor Computation Stage (DSP Processor). |
| Digital to Analogue Conversion Stage. |
| (One can refer to Fig1 to see these stages) |
A) Analogue to Digital Conversion (ADC) Errors |
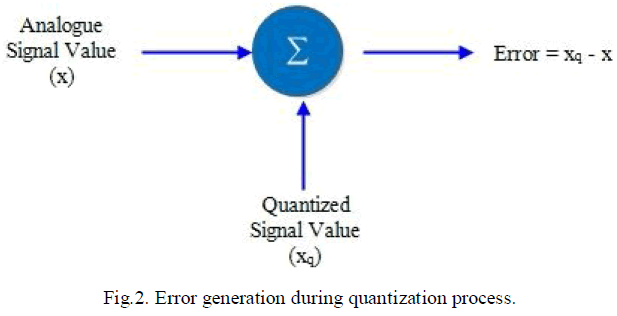
| 1. Quantization Error: Quantization is a process by which an analogue signal (which has been sampled and held at a constant value) is approximated to one of the set of values meant to represent the signal. This set of values is dependent on the number of bits used to represent the signal. For example with 2 bits a signal can have four levels at which the value can be approximated to during quantization and with three bits a maximum of 8 levels can represent the signal. Thus some analogue values are assigned approximate values since not all analogue signal values can be represented. This difference between analogue signal and its digital representation after quantization is called Quantization Error. Quantization error is illustrated by the simplified diagram of Fig2. Quantization errors can be classified into Rounding/Round off error and Truncation/Truncating error depending on whether the signal is approximated to a quantization level which is above or below it.` |
 |
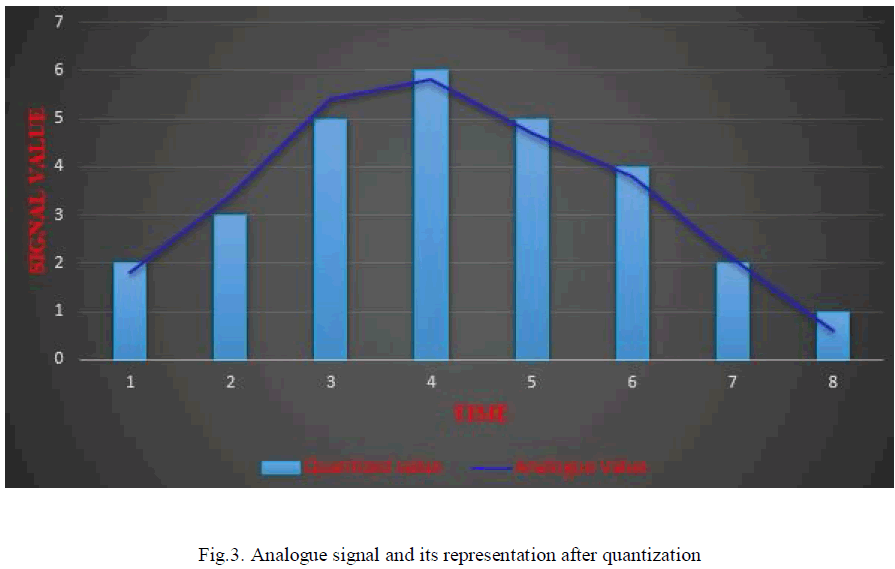
| Rounding/ Round off Error: If an analogue signal is assigned/ approximated to a quantization level value which is higher than the original analogue signal then the error incurred is known as the rounding or round off error. Consider Fig3 which shows the representation of an analogue signal and also its representation after quantization for a situation where eight samples of the signal are to be taken. Eight quantization levels for the representation of the signal using 3 bits are implemented i.e. digital 000 to 111 as illustrated by 0 to 7 on the y-axis. By looking at TIME (4) and TIME (5), |
| for example, the original signal is assigned to a higher quantization level and a rounding error is said to exist. If the difference between two quantization levels is taken as Δ then the rounding error is limited to ± Δ / 2. |
| Truncation Error: If the analogue signal above the nearest quantization level is dropped then a truncation error has occurred. By looking at Fig3 at TIME (2) and TIME (3), for example, the signal has been approximated to a level which is of lower value than the original analogue signal resulting in a truncation error. |
 |
| B) Errors in Computation: These are errors which can be incurred while performing operations on digital data in the DSP Processor. Some common sources of error are: |
| 1) Number Format use: In DSP the signals are represented as discrete sets of numbers and two typical formats for these numbers are a) Fixed Point Format and b) Floating Point Format. In fixed point format the number is represented as an integer or a fraction by use of a fixed number of bits. Thus in fixed point representation we have Fixed Point Integer representation as well as Fixed Point Fractional representation. |
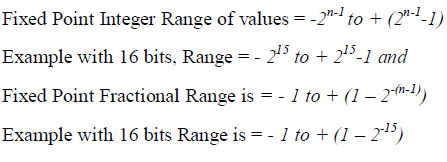 |
| The multiplication of numbers can produce a value which requires more number of bits to represent it and in the event of fixed point format an overflow error can occur. This problem is more inherent in fixed point integer multiplication. Consider a 3-bit fixed point integer format |
 |
| (Value is inside range although precision has been lost. The LSBs have to be discarded and result approximated to ½). As a result overflow error has been traded for rounding error by representing in fractional rather than integer fixed point format. |
| Floating Point Number format: In most cases DSP computations result in growth of computed values and in some cases the growth is unpredictable. As a result a large number of bits may be required to represent the signal to give allowance for signal growth. Example is the multiply and Accumulate (MAC) function. However a processor architecture does not allow for unlimited number of bits. As such, some processors use floating point format for signal processing computations. The commonly used floating point format is the IEEE754. The format consists a Sign bit, Exponent and Mantissa as shown in Fig4 for 32 bit number representation. |
 |
| Floating point implies that the radix (decimal point) can be placed anywhere relative to the significant digits if a number. Multiplying 2 floating point numbers will give: |
| Thus floating point multiplication requires addition of exponents and multiplication of mantissas whilst floating point addition requires exponents to be normalized before the addition. |
| 2) Overflow Error: Overflow error, as stated earlier on, occurs if a result of a computation cannot be held in the accumulator. This may result in wraparound error if necessary correctional procedure is not carried out. Wraparound is when after the highest possible positive value the result goes to the most negative value and vice versa leading to erroneous output. |
| C) Digital to Analogue Conversion Errors: Typically digital to analogue converters use fewer bits to represent the digital signal from the DSP processor. As a result truncation and rounding off of data will exist leading to the truncation error and rounding error similar to those found in analogue to digital converters. Another form of error is that the output of the D/A converter is not ideally reconstructed. In many cases the output of DSP processor is fed to a zero order hold circuit which will also feed to the reconstruction filter. The zero order hold module holds data which will maintain the input to reconstruction filter constant during the period between successive data samples. A situation exists whereby the input to the reconstruction filter is like the convolution of the DSP processor output samples with a unit pulse of width equivalent to sampling interval. The effect of this convolution is the reduction in amplitude of analogue signal output. |
RESULTANT SOLUTIONS: ERROR MINIMIZATION |
| The discussion which follows aims to bring solutions to the above named sources of error i.e. how they can be eliminated or in some way greatly reduced. |
| 1) Quantization Error: Quantization error can be reduced by increasing the number of bits used to represent the analogue signal. This will result in more quantization levels available to represent the signal such that the signal is approximated to an almost identical level as its original value. The resolution of the system also increases. |
| 2) Overflow Error: Errors due to overflow can be solved by use of Guard bits. These are extra bit which are used to accommodate overflow bits. For example if four guard bits are added they ensure that there is no overflow for up to 16 accumulations. Another alternative measure is to introduce saturation to the system. This method involves sticking the output to the most negative or most positive value if saturation is about to occur. For example if result exceeds maximum positive value, the output won’t saturate to the most negative value but will saturate/stick at the most positive value. |
| 3) Number formats: If numbers are to be represented in fixed point integer format then the range can be increased by doubling the number of bits to come out with a Double-Precision Fixed Point Integer format. However more storage will be required for the same data and number of accesses may need to be doubled if the original size of data bus is used. Also for fixed format presentation, overflow can be reduced if numbers are represented in fixed point fractional rather than fixed point integer format. |
| 4) Reconstruction Filter: This filter can be designed such that its frequency response which is the inverse of the frequency response of the convolving pulse. This filter ids placed at the output of the Digital to Analogue converter and will compensate for the amplitude reduction of the D/A converter due to the zero order hold circuit. |
CONCLUSIONS |
| This analysis has brought about a generalized and broad view of the errors involved in digital signal processing systems. This analysis aims to be a stepping stone to all those being inducted to digital signal processing system as it gives an overview of the errors irrespective of the type of application the signal processing is being implemented. With this generalized view it becomes simpler as one advances with this signal processing applications to become aware of the immediate possible causes of error. As one advances into a specialization area, say avionics, medical equipment, industrial control, etc. then it becomes easier to appreciate these error sources and become aware as one embarks in the design process. |
References |
|