International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Menu

ISSN ONLINE(2320-9801) PRINT (2320-9798)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Transmission of Data between Sensors by devolved Recognition

K.G.S. Venkatesan1, B. Sundar Raj2, V.Keerthiga3, M.Aishwarya4
  1. Research Scholar, Dept. of C.S.E., Bharath University, Chennai, India.
  2. Research Scholar, Dept. of C.S.E., Bharath University, Chennai, India.
  3. Department of C.S.E, Bharath University, Chennai, Tamil Nadu, India.
  4. Department of C.S.E, Bharath University, Chennai, Tamil Nadu, India.
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Abstract

This paper presents a model of the property of a Wireless detector Network (WSN) deployed over asq. space, that considers border effects. This model supports AN correct analysis of the dependability of the network with and while not node failures. exploitation the planned model we tend to analyse the trade-off between the amount of sensors and their communication vary once deploying a wireless network that's connected with high chance and validate this analysis through simulation experiments. further simulations, considering detector failures, sanctioned that periodic detector redeployments, calculated in line with the planned model, will extend the dependability of WSNs, keeping them connected with high chance. For applications which will face up to temporary network disconnection, we tend to obtained theoretical and experimental proof that the planned model additionally supports the calculation of a less frequent redisposition procedure that has network property at high levels of convenience, finally, extending the approach to a circular formed space.

Keywords
Wireless device networks, dependableness, accessibility, network property, border effects, Fault tolerance.

INTRODUCTION
WIRELESS sensing element networks (WSNs) became popular thanks to however simply and quick they'll be deployed in inaccessible terrains, in locations of emergency operations and in alternative dangerous environments. Consequently, the amount of applications of those networks in crucial areas like military, security, and telecommunication systems, business automation and management, health and several other others [1], has inflated considerably. Most current wireless sensing element networks encompass an outsized range of tiny, lowcost, low-power, failure-prone sensing element nodes that utilize multi-hop communication over a wireless channel and operate [3].
Sensors in WSNs collect data from the surroundings and should transmit the aggregative collected knowledge to a specified entree. Therefore, the correct operation of the network depends on the reliable transmission of data by its sensors and to the multi-hop communication nature of WSNs, as pare condition for reliable data transmission is full multi-hop property of the network. A network is absolutely multi-hop connected once it's a minimum of one wireless multi-hop path linking every sensing element node to every alternative sensing element node. Our fourth and last contribution is that the analytical ability to fine tune the referred sensing elementary disposition amount and size therefore on come through a needed level of network accessibility [5].
The remainder of this paper is organized as follows. II presents the network model and lists antecedent famed results associated with the property of wireless sensing element networks [2]. In III we tend to discuss associate analytical analysis of border effects in wireless sensing element networks, deferring the mathematical details to the Appendix. Sections IV and V the results of our work. We tend to address the difficulty of manufacturing a connected sensing element wireless network, whereas the preservation of network property within the presence of sensing element failures is addressed in Section V in 2 cases: with regard to reliableness and with regard to accessibility. Section VI discusses extending the approach to a circular space [9].
This paper extends our previous work bestowed in [7]. It includes further simulation experiments associated an increased analysis of the tradeoffs between the quantity of sensors and their communication point order to stay the network totally connected. It additionally presents and compares 2 various solutions for guaranteeing a connected WSN upon readying, the corner border dominance answer [10].

II. LITERATURE SURVEY
Decentralized fault diagnosis for sensor networks, The problem of fault diagnosis for sensor networks. We examine faults that involve an anomalous behaviour of the sensor and investigate their diagnosis only through the local interaction between faulty nodes and healthy ones. We provide heuristics to actively diagnose faults and recover the nominal behaviour.
Reliable data fusion in wireless sensor networks under byzantine attacks, Byzantine attacks in wireless sensor networks with mobile access (SENMA) points is considered .By exploiting the approximately linear relationship between the scheme parameters and the network size, we propose a simplified q-out-of-m scheme which can greatly reduce the computational complexity, and at the same time keeping good performance. We show that for a fixed percentage of malicious sensors, the detection accuracy of the simplified q-out-of-m scheme increases almost exponentially as the network size increases. Second, we propose a simple but effective method to detect the malicious sensors before decision making.
Robust distributed spectrum sensing incognitive radio networks, Cognitive radio is an enabling technology for efficient utilization of radio spectrum. A key function of cognitive radios is spectrum sensing, which enables secondary users to identify vacant spectrum not used by primary users. A cognitive radio network that employs a distributed spectrum sensing framework. Analysis and simulation results show that WSPRT can guarantee the accuracy of sensing results even when a considerable number of secondary users are reporting false sensing information.
Correspondence channel aware decision fusion in wireless sensor networks, Information fusion by utilizing multiple distributed sensors is studied in this work. Extending the classical parallel fusion structure by incorporating the fading channel layer that is omnipresent in wireless sensor networks, To address this issue, two alternative fusion schemes, namely, the maximum ratio combining statistic and a two-stage approach using the Chair–Varshney fusion rule, are proposed that alleviate these requirements and are shown to be the low and high signal-to-noise ratio (SNR) equivalents of the likelihood-based fusion rule.
Fusion of decisions transmitted over rayleig fading channels in wireless sensor networks, The problem of fusing decisions transmitted over fading channels in a wireless sensor network. Based on the assumption that all the sensors have the same detection performance and the same channel signal-to-noise ratio (SNR), when the channel SNR is low, this fusion rule reduces to a statistic in the form of an equal gain combiner (EGC), which explains why EGC is a very good choice with low or medium SNR.
Industrial grade wireless base station for wireless sensor networks, We present the design and development of an industrial grade wireless base station for industrial monitoring and control using wireless sensor networks. Although a wireless sensor node is efficient enough to act as a base station in a wireless sensor network their processing power and communication capabilities are limited since they are designed to work at very low power. It also provides excellent operation in the industrial environment with an operating temperature range of -40 to +85 C.
Routing in wireless sensor networks, A sensor networks is a system that consists of thousands of very small stations called sensor nodes. The main function of sensor nodes is to monitor, record and notify a specific condition at various locations to other stations and end users. The protocols are AODV and DSCV. The interpreted results clearly show that DSCV is the best protocol for our simulation.
Distributed energy-adaptive routing for wireless sensor networks, Most routing algorithm for sensor networks focus on finding energy efficient paths to prolong the lifetime of sensor networks. Therefore ,ideally, routing algorithms should consider not only energy efficiency, but also the amount of energy remaining in each sensor, thus avoiding nonfunctioning sensors due to early power depletion.

III. NETWORK MODEL
The network model thought of during this study consists of N sensing element nodes uniformly deployed over a sq. space A of size L. Sensors transmit and receive equally all told directions with a standard, fastened most power setting, here referred to as the most communication vary R [12]. This network are often sculptured as AN adrift graph G (V; E) that consists of a collection of vertices V, resembling the sensing element nodes, and a collection of edges E, resembling the communication links between the nodes. Characterizing dist(u; v) because the physical distance between nodes u and v, E is outlined as follows:
E=f(u;v)2V2jdist(u;v)Rq
It is additionally assumed that the network is static (sensors ar stationary), that every one links between any try of nodes are duplex or regular, which there aren't any radiopaque obstacles within the space. A node is claimed to be isolated if there aren't any different nodes among its communication vary. The network is multi-hop, as sensors get together to route every other’s messages [15]. Finally, the network is k-connected if there square measure k disjoint communication ways connecting every node to every and each different node. The network is connected if there's a minimum of one multi-hop communication path connecting every node.
The likelihood that a node is isolated (d = 0) is given by:
P (d = 0) = e R2
which is capable the node’s coverage space R2 increased by the expected node density [13] . The chance that every node has a minimum of d0 neighbours, i.e., the network includes a minimum node degree d0, is given by:
Based on the works of Penrose [8], on geometric random graphs, and of Bollobas´ [9], on typical random graphs, it will be declared that, if N is high enough, then with high likelihood, a network pictured by a graph G(V; E) is kconnected if its minimum node degree dmin is capable k [12]. Thus, for k = 1, one will say that the network is connected if its minimum node degree dmin is a minimum of capable one. That is:
P (G is k-connected) = P (dmin k)
for P (dmin k) = one, i.e., once the likelihood that the minimum network degree is larger or adequate is close to one. exploitation Equations two and three this could be declared as
P(G is connected)=1 e R2N =1 e Ed N(4)

IV. ANALYTICAL EVALUATION OF BORDER EFFECTS
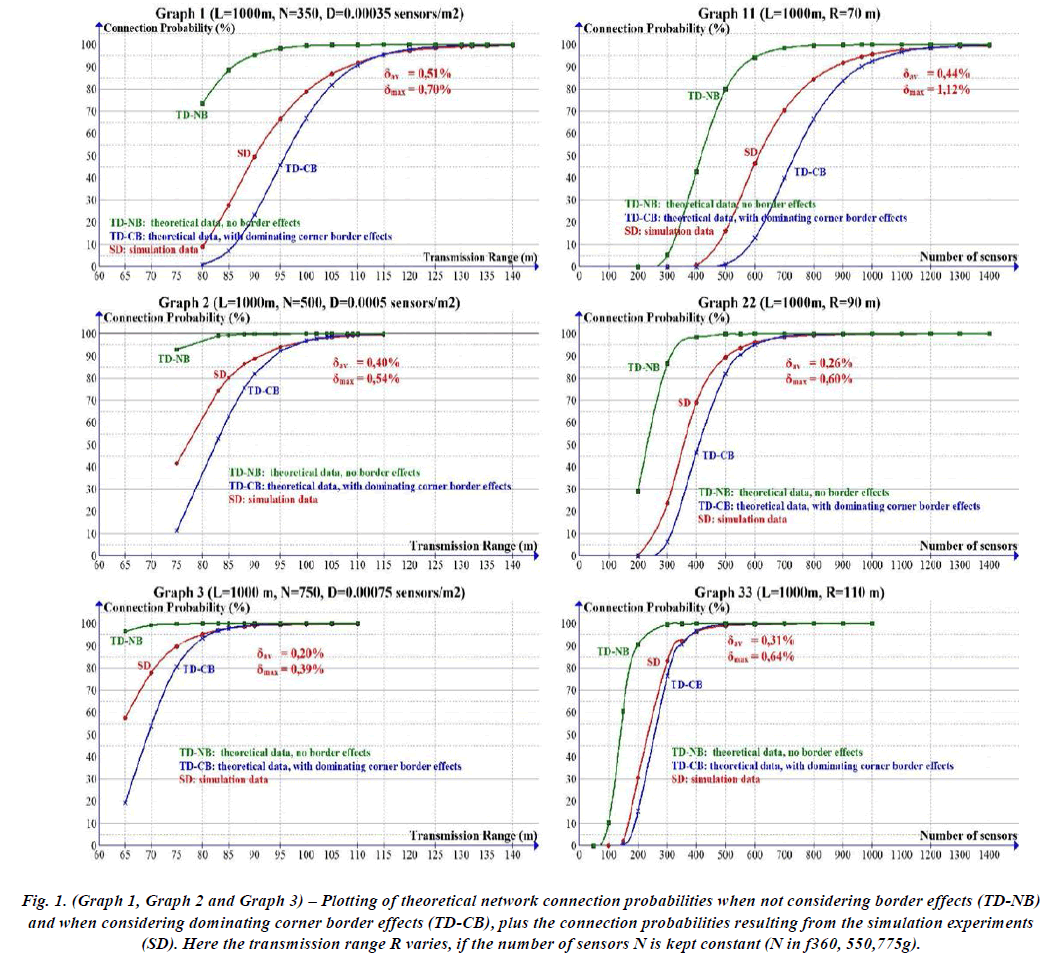
The Analytical equations bestowed within the previous section are valid below the idea of a network space A taken from an infinitely massive two-dimensional space inhabited with node density = N=A. The results of this assumption is that every one nodes are thought-about as having constant effective variety of neighbours of R2.
This is obviously a perfect condition that doesn't correspond to real networks deployed in real environments. So, we proceed to perform Associate in Nursing analysis that considers border effects so as to raised approximately [13]. Given a sq. space of facet L, the borders correspond to regions B and C. we tend to decision the oblong region B the lateral border, the sq. region C the corner border, and also the sq. region I the inner region. For a sensing element node settled within the inner region of the network space the effective variety of neighbours is so given by R2, as explicit by Equation one. This results from the very fact that the effective coverage space of a degree within the inner region is exactly adequate R2 [19].
It may be seen from, however, that the effective coverage space, for some extent within the border regions B or C, is a smaller amount than R2. Consequently, the effective range of neighbours of device nodes set within the border areas are going to be smaller than R2. As network property properties rely on the expected effective range of neighbours of the device nodes (Equation 4), getting the worth of the expected effective range of neighbours of device nodes in these regions is prime to grasp the property properties of a true device network [16]. This section investigates this drawback. A sq. network space was chosen initially as a result of most authors operating during this space targeted on this form in their analysis, that is additional simple for validation functions. As a result, an instantaneous comparison would be potential [20].
image
Our approach for the analysis of border effects. We currently commit to calculate the effective range of neighbours of a sensing element node within the border regions B and C.
image
The calculations mentioned within the 2 preceding paragraphs square measure shown well within the Appendix. They yield:
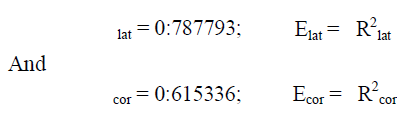image
Having obtained the expected effective variety of neighbours (node degree) for nodes within the border regions, Elat and Ecor, we will calculate disfunction , the expected effective node degree of the complete network region A.

V. DEPLOYING A CONNECTED NETWORK
The next step is to know a way to apply the results for Elat and Ecor, the expected effective node degrees within the lateral and corner border regions, to deploy a connected network with high chance during this section we tend to take into account and analyse 3 doable solutions for this [25] .

A. Weighed border effects model
First formulate a hypothesis to elucidate however the border effects (represented by Elat and Ecor)have an effect on the property of the network and so check our hypothesis by suggests that of simulation experiments [24]. we tend to assume that the expected effective node degree for the network, maleerecticle dysfunction is up to the weighted average of the values of male erecticle dysfunction, Elat and Ecor, with weights up to the areas of the inner region, the lateral border and corner borders, severally. this offers us:
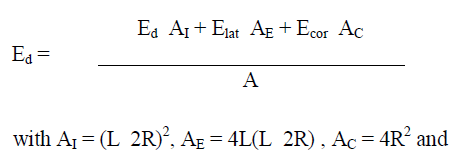image
A = R2.
Substituting the area and expected node degree values.
image

B. Corner border dominance model
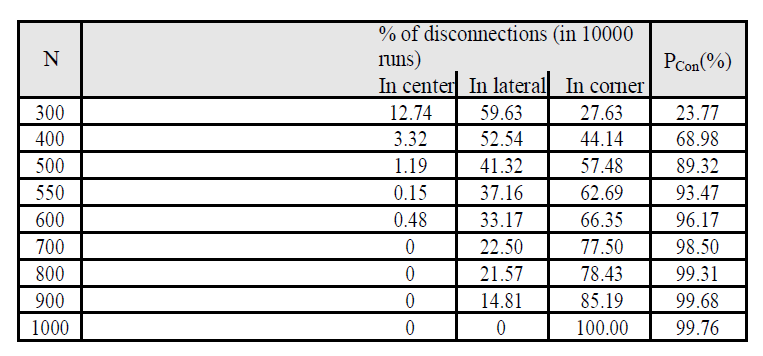
The results of those experiments, shown in Tables I and II , point that, for top affiliation possibilities(high node densities and/or giant node communication ranges), most disconnections happen within the corner borders; that's, the node degree within the corner borders, being the littlest, dominates over the node degrees within the lateral border and therefore the central region of the network space [29]. Thus if we might approximate the effective node degree of the network space as adequate to the node degree within the corner borders, we might get a boundary worth for the network property, that ought to be very close to reality in conditions of high connectivity probabilities. We attempted to formalize this by making:
EdEcor; P (network is connected) 1 eEcorN and, for P (network is connected) close to 1, we obtain:
P (network is connected) 1 eEcorN
We run new simulation experiments victimisation L = one thousand m, with constant N and ranging values of R, to live the chance of getting a connected network. totally different values of N were chosen within the set f360, 550,775g to watch however the variation of R influenced the results for various (but constant) values of N. every experiment was perennial ten thousand times for higher accuracy [30].

VI. PROPOSED SYSTEM
Information Sharing Among Sensors on Decentralized Detection Set of sensors transmits a highly compressed summary of its observations (a binary message) and subsets of the sensors to both (star and parallel) transmit their messages to the fusion center [17]. We have proved that the daisy chain architecture introduced and analyzed in this paper performs no better (in the sense of the asymptotically optimal Neyman–Pearson error exponent) than a star architecture with the same number of sensors and observations. Our main result was given for the case where the number of sensors in the first and the second stage of the daisy chain architecture is the same (and grows with the total number of sensors in the architecture) [18].

A.User Authentication
To share the information from one node to another node we have to access the user authentication. Other than Admin no one can access the sensor process [25].

B.Sensor Communication
There are two ways in Sensor Communication One is Dual and the other is Full. Dual and full both does the same work with some modifications. In Dual, the node to node data transfer will be done but we can’t able to know which sensor is connected to which node. In Full way communication, the same data transfer will be done but we can able to know which sensor is connected to which node [28].

C.Sharing
In this module, data is transmitted form one node to another then the sensor will be activated. If again the data transmitted form the second node to the third node and if the first sensor gets deactivated, automatically the second sensor will be activated [30].

D.Works of Sensor
First we have to create the sensors. After creating the sensors we can view the sensing range. We can also see the communication range in this module [12].

VII. CONCLUSION AND FUTURE WORK
We have investigated the reliableness of wireless detector networks (WSNs) with reference to network property and sensor node failures. so as to know additional exactly the knowledge, this is often conjointly a unique contribution provided by our analysis. we have a tendency to run further experiments simulating a network subject to detector failures and obtained experimental MTTD and MNSR values that were terribly near the analytically derived ones. These experiments diagrammatic the fourth contribution of our work, that a detector redisposition specified by the size-period try (No MNSR, MTTD) can guarantee a extremely accessible network for applications that can endure short non-connectivity periods [31].

VIII. ACKNOWLEDGEMENT
The author would like to thank the Vice Chancellor, Dean-Engineering, Director, Secretary, Correspondent, HOD of Computer Science & Engineering, Dr. K.P. Kaliyamurthie, Bharath University, Chennai for their motivation and constant encouragement. The author would like to specially thank Dr. A. Kumaravel for his guidance and for critical review of this manuscript and for his valuable input and fruitful discussions in completing the work and the Faculty Members of Department of Computer Science &Engineering. Also, he takes privilege in extending gratitude to his parents and family members who rendered their support throughout this Research work.

References
  1. J. L. Bredin, E. D. Demaine, M. Hajiaghayi, and D. Rus, “Deploying sensor networks with guaranteed capacity and fault tolerance,” in Proceedings of the 6th ACM International Symposium on Mobile Ad Hoc Networking and Computing, ser. MobiHoc ’05. New York, NY, USA: ACM, 2005, pp. 309–319.
  2. Hoff and U. Wehling, “Reconciliation of structured data in multihopmanets.” in MoMM, G. Kotsis, D. Taniar, E. Pardede, and I. K. Ibrahim, Eds., vol. 215. Austrian Computer Society, 2006, PP. 281–290. 3. J. Yoon, M. Liu, and B. Noble, “Random waypoint considered harmful,” in IEEE INFOCOM 2003. Twenty-second Annual Joint Conference of the IEEE Computer and Communications Societies (IEEE Cat. No.03CH37428), vol. 2. IEEE, 2003, PP. 1312–1321.
  3. C. Bettstetter, “On the minimum node degree and connectivity of a wireless multihop network,” in Proceedings of the 3rd ACM International Symposium on Mobile Ad Hoc Networking &Amp; Computing, ser. MobiHoc ’02. New York, NY, USA: ACM, 2002, PP. 80–91.
  4. K.G.S. Venkatesan. Dr. V.Khanna, Dr. A.Chandrasekar, “Autonomous system for mesh network by using packet transmission & failure detection”, Inter. Journal of Innovative Research in computer & comm. Engineering, Vol . 2 , I s su e 1 2 , De c emb er - 2014.
  5. M. Brust, C. Ribeiro, and J. Filho, “Border effects in the simulation of ad hoc and sensor networks,” in Computer Modelling and Simulation, 2009. UKSIM ’09. 11th International Conference on, March 2009, PP. 180–185.
  6. K.G.S. Venkatesan and M. Elamurugaselvam, “Design based object oriented Metrics to measure coupling & cohesion”, International journal of Advanced & Innovative Research, Vol. 2, Issue 5, PP. 778 – 785, 2013.
  7. M. Matsumoto and T. Nishimura, “Mersenne twister: A 623-dimensionally equidistributed uniform pseudo-random number generator,” ACM Trans. Model. Comput. Simul., vol. 8, no. 1, PP. 3–30, Jan. 1998.
  8. Sathish Raja and K.G.S. Venkatesan, “Email spam zombies scrutinizer in email sending network infrastructures”, International journal of Scientific & Engineering Research, Vol. 4, Issue 4, PP. 366 – 373, April 2013.
  9. G. Bianchi, “Performance analysis of the IEEE 802.11 distributed coordination function,” IEEE J. Sel. Areas Commun., Vol. 18, No. 3, PP. 535–547, Mar. 2000.
  10. K.G.S. Venkatesan, “Comparison of CDMA & GSM Mobile Technology”, Middle-East Journal of Scientific Research, 13 (12), PP. 1590 – 1594, 2013.
  11. P. Indira Priya, K.G.S.Venkatesan, “Finding the K-Edge connectivity in MANET using DLTRT, International Journal of Applied Engineering Research, Vol. 9, Issue 22, PP. 5898 – 5904, 2014.
  12. J. P. Coon, C. P. Dettmann, and O. Georgiou, “Full connectivity: Corners, edges and faces,” Journal of Statistical Physics, Vol. 147, No. 4, PP. 758– 778, 2012.
  13. K.G.S. Venkatesan and M. Elamurugaselvam, “Using the conceptual cohesion of classes for fault prediction in object-oriented system”, International journal of Advanced & Innovative Research, Vol. 2, Issue 4, pp. 75 – 80, April 2013.
  14. Ms. J.Praveena, K.G.S.Venkatesan, “Advanced Auto Adaptive edge-detection algorithm for flame monitoring & fire image processing”, International Journal of Applied Engineering Research, Vol. 9, Issue 22, PP. 5797 – 5802, 2014.
  15. A. Eslami, M. Nekoui, H. Pishro-Nik, and F. Fekri, “Results on finite wireless sensor networks: Connectivity and coverage,” ACM Trans. Sen. Netw., vol. 9, no. 4, pp. 51:1–51:22, Jul. 2013.
  16. K.G.S. Venkatesan. Dr. V.Khanna, “Inclusion of flow management for Automatic & dynamic route discovery system by ARS”, International Journal of Advanced Research in computer science & software Engg., Vol.2, Issue 12, PP. 1 – 9, December – 2012.
  17. Needhu. C, K.G.S.Venkatesan, “A System for Retrieving Information directly from online social network user Link ”, International Journal of Applied Engineering Research, Vol. 9, Issue 22, PP. 6023 – 6028, 2014.
  18. M. Grottke, H. Sun, R. Fricks, and K. Trivedi, “Ten fallacies of availability and reliability analysis,” in Service Availability, ser. Lecture Notes in Computer Science, T. Nanya, F. Maruyama, A. Pataricza, and M. Malek, Eds. Springer Berlin Heidelberg, 2008, vol. 5017, PP. 187– 206.
  19. K.G.S. Venkatesan, R. Resmi, R. Remya, “Anonymizimg Geographic routing for preserving location privacy using unlinkability and unobservability”, International Journal of Advanced Research in computer science & software Engg., Vol. 4, Issue 3, PP. 523 – 528, March – 2014.
  20. Selvakumari. P, K.G.S.Venkatesan, “Vehicular communication using Fvmr Technique”, International Journal of Applied Engineering Research, Vol. 9, Issue 22, PP. 6133 – 6139, 2014.
  21. K.G.S. Venkatesan, G. Julin Leeya, G. Dayalin Leena, “Efficient colour image watermarking using factor Entrenching method”, International Journal of Advanced Research in computer science & software Engg., Vol. 4, Issue 3, PP. 529 – 538, March – 2014.
  22. L. A. Laranjeira and G. N. Rodrigues, “Extending the reliability of wireless sensor networks through informed periodic redeployment.” in SERE. IEEE, 2012, pp. 167–176.
  23. K.G.S. Venkatesan. Kausik Mondal, Abhishek Kumar, “Enhancement of social network security by Third party application”, International Journal of Advanced Research in computer science & software Engg., Vol. 3, Issue 3, PP. 230 – 237, March – 2013.
  24. Annapurna Vemparala, K.G.S. Venkatesan, “Routing Misbehavior detection in MANET’S using an ACK based scheme”, International Journal of Advanced & Innovative Research, Vol. 2, Issue 5, PP. 261 – 268, 2013.
  25. K.G.S. Venkatesan. Kishore, Mukthar Hussain, “SAT : A Security Architecture in wireless mesh networks”, International Journal of Advanced Research in computer science & software Engg., Vol. 3, Issue 3, PP. 325 – 331, April – 2013. 27. Annapurna Vemparala, K.G.S. Venkatesan, “A Reputation based scheme for routing misbehavior detection in MANET”S ”, International Journal of computer science & Management Research, Vol. 2, Issue 6, June - 2013.
  26. K.G.S.Venkatesan, “Planning in FARS by dynamic multipath reconfiguration system failure recovery in wireless mesh network”, International Journal of Innovative Research in computer & comm. Engineering, Vol . 2 , I s su e 8 , Au gu st - 2014.
  27. F. Fabbri, C. Buratti, and R. Verdone, “A multi-sink multi-hop wireless sensor network over a square region: Connectivity and energy consumption issues”, in GLOBECOM Workshops, 2008 IEEE, PP. 1–6, November – 2008.
  28. R. Bhatt and R. Datta, “Redeployment strategies for wireless sensor networks under random node failures and budget constraints,” in Parallel Distributed and Grid Computing (PDGC), 2012 2nd IEEE International Conference on, PP. 767–772, December – 2012.
  29. G. Mao and B. D. O. Anderson, “Towards a better understanding of large-scale network models,” IEEE/ACM Trans. Network., Vol. 20, No. 2, PP. 408–421, 2012.