ISSN ONLINE(2320-9801) PRINT (2320-9798)
ISSN ONLINE(2320-9801) PRINT (2320-9798)
S. Saranya1, R. Priya Vaijayanthi2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering
The travelling salesman problem is said to be an NP-hard problem in combinatorial optimization, important in research and theoretical computer science. Bio- inspired algorithms such as Ant colony Optimization, Bee Colony Optimization, cuckoo Search Optimization three algorithms were used and their performances are compared to obtain solution. The main objective is to find a cyclic permutation that minimizes the cost of visiting every node only once. And reduce the complexities faced in existing. Provide the optimal result for the travelling salesman problem. In this paper we present techniques to solve this problem, a tabu search based algorithm and bio algorithm. The results of both techniques are shown and compared to decide which one of the two alternatives gets better results. A dynamic nearest neighbourhood search method used to solve combinatorial optimization problems.
KEYWORDS |
| Np-hard problem, optimization, and neighbour search |
I. INTRODUCTION |
| Travelling salesman problem (TSP) consists of finding the shortest route in complete weighted undirected graph G with n nodes; so that the start node and the end node are identical and all other nodes in this tour are visited exactly only once. The most popular practical example of TSP are: regular distribution of goods or resources, finding of the shortest of costumer using path, planning bus way etc., but also in the areas that have nothing to do with travel routes. TSP is said to be one of the NP hard optimization problems. Np-hard problem describes a solution is obtained from a set of decision problem; solution may be in polynomial order. In TSP, the salesman travels all the cities at once and returns to the starting city and keeping the entire possible shortest route within reasonable execution time. The Travelling Salesman Problem (TSP) is one of the major problems, which has been addressed extensively by Mathematicians and computer scientists. Its importance stems from the fact there is a plethora of fields in which it finds applications such as DNA fragment assembly, VLSI design. For example, given a finite set of cities and the cost of travelling from city i to city j, if a travelling salesman were to visit each city exactly once and then return to the home city. |
| Travelling Salesman Problem (TSP) is about finding a Hamiltonian path with minimum cost. It is common in areas such as logistics, transportation and also in semiconductor industries. For instance, finding an optimized scan chains route in integrated chips testing, parcels collection and sending in logistics companies, are some of the practical approach for TSP. Efficient solution to such problems will ensure the tasks are carried out effectively and thus increase its growth. Due to its importance it is useful in many industries; TSP is still being practiced by researchers from various disciplines. Many heuristic optimizations Methods are developed for searching nearly optimal solution in solving TSP such as Genetic Algorithm (GA), Particle Swarm Optimization (PSO), Ant Colony optimization (ACO), Simulated Annealing (SA) and Artificial Bee Colony (ABC).Ant colony optimization (ACO) is one of the most successful techniques in the wider field of swarm intelligence. Many research works have been carried out to ant colony optimization techniques in different areas. It is a relatively to the Meta-heuristic Technique and has been successfully used in many applications especially problems that belongs to the Combinatorial optimization. |
| The vehicle routing problem (VRP) is a combinatorial optimization Implicit is the goal of minimizing the cost of distributing the goods. Vehicle Routing Problem with Pickup and Delivery (VRPPD) is describes, a number of goods need to be moved from certain pickup locations to other destination place. The goal is to find best routes for a fleet of vehicles to visit the pickup and drop-off locations ACO inspired by the foraging behaviour of real ant was first introduced by dorigo and his colleagues and has become one of the most efficient algorithms for TSP. Ant colony optimization is an essential technique to find best paths through graphs. ACO is based on the pheromone trail laying and following behaviour of some ant Species, a behaviour that was shown to allow real ant colonies to find shortest paths between their colony and food sources. ACO has been widely applied to solving various combinatorial optimizations Problems such as travelling salesman problem (TSP), job-shop scheduling problem (JSP), vehicle routing problem (VRP). |
| Ant Colony Optimisation can be used to find the solutions of difficult combinatorial optimization problems and it has its rapidly growing popularity. Although ACO has a powerful capacity to find out solutions to combinatorial optimization Problems, it has the most difficult problems such as of stagnation and premature Convergence and the convergence speed of ACO are always slow. Those problems will be more obvious when the problem size increases. The best performing ACO algorithms for the TSP improve the solutions generated by the ants using local search algorithms. Some behaviour in animals has the potential to be adapted to find TSP. An example is highly coordinated Patterns shown in bee and ant foraging behaviour. Ants deposit a chemical substance known as pheromone along the way between their colony and food source. Another approach to solve optimization problem is, Bee colony optimization. Bees perform waggle dance upon returning to their starting position when they found a food source. Pheromone trail and waggle dance are used as a communication medium among individuals in ant or bee colony system. These individuals can perform their actions (performing waggle dance) locally with limited knowledge about the entire system. When their local actions are combined, they will produce global effects such as directing more individuals to the new discovery of food source. |
II. RELATED WORKS |
| Travelling salesman problem with related algorithms starts with an initial solution, called initial state, which is modified during execution in order to find a near optimal solution. In initialization Functions, starting with a partial path and building step by step the initial solution. Nearest Neighbour search function begins by selecting a random node as a starting node. Then iteratively, the nearest node is found out until last node is reached and the path or node is added to the partial path. Insertion function starts the process with a result of previous step such as partial path consisting of two cities. These cities are the closest on the map. This means that the process starts with the shortest edge. From this point and iteratively, the nearest node to any node in the partial path is obtained. This node is inserted into the path at the position that case, the node farthest from any of the nodes involves lower cost increase function. In this that is already in the partial path is taken as the node to insert. After that, the node is inserted into the position that involves lower cost increase. |
| The traveling salesman problem is said to be an NP-hard problem in combinatorial optimization, important in practical research and theoretical computer science. Thus here implementing a technique to show the improved result in traveling salesman problem. We also performed some determination of certain aspects of the algorithms for “tabu search and genetic” algorithms. |
| 2.1 TRAVELLING SALESMAN PROBLEM |
| Given a set of cities and the distance between each possible path, the Travelling Salesman Problem is to find the best possible way of ‘visiting all the cities exactly once and returning to the starting point’. As TSP is a NP hard problem it is often used as a benchmark for optimization techniques. The sequential ordering problem deals with the problem of visiting a set of cities where precedence relations between the cities exist. The objective is to find a route between a subset of the cities, which minimizes total cost and reduces the resources used. The travelling salesman problem is wide spread in engineering applications. It has been used in designing hardware devices and radio electronic devices, especially for communications, in the architecture of many networks, etc. In this technique is additionally used for, some industrial problems such as device scheduling, cellular manufacturing and frequency assignment problems can be formulated as a TSP. The Travelling Salesman Problem is one of the best known NP-hard problems, which means that there is no exact algorithm to solve it in polynomial sequence. The minimal expected time to obtain an optimal solution is exponential. From set of feasible solutions usually use heuristics to help us to obtain a “good” Solution. |
| 2.2 TABU SEARCH |
| Tabu search is another method to solve the traveling salesman problem as the genetic algorithm performs which finds good solution for combinatorial optimization problems. The forbidden movements are normally stored in a list called the tabu list. Whenever the successor’s generation function is going to make a movement, that is, a change in the current state, the tabu list is verified or to check whether the movement is forbidden. If it is, the movement is discarded and another one is tried. When an allowed movement is found, the new state is accepted and the movement is stored in the list to prevent the algorithm from visiting the same state in a near future. |
| The choice of algorithm is influenced by the priorities of the user. The tabu search algorithm begins with an nearest neighbour search. Then iteratively, the current state will be modified by generation function with the aim of finding better solutions. The tabu search is an algorithm designed to find good solutions for combinatorial optimization problems. It is one of the most widely known Meta heuristics, due to the quality of its solutions. Tabu accepts optimal solution as well as non optimal solution. It performs transformation and it prohibits reverse transformation. There is no an optimum size for the tabu list, because this depends on the size of the instance, the successors generation function and the movement prohibition criteria. The tabu search algorithm has the property of accepting worse solutions than the current one, with the aim of avoiding premature local optima. To prevent premature optima problem, there is a structure called memory. This structure is used to prevent the search from re-visiting solutions visited in the immediate past. |
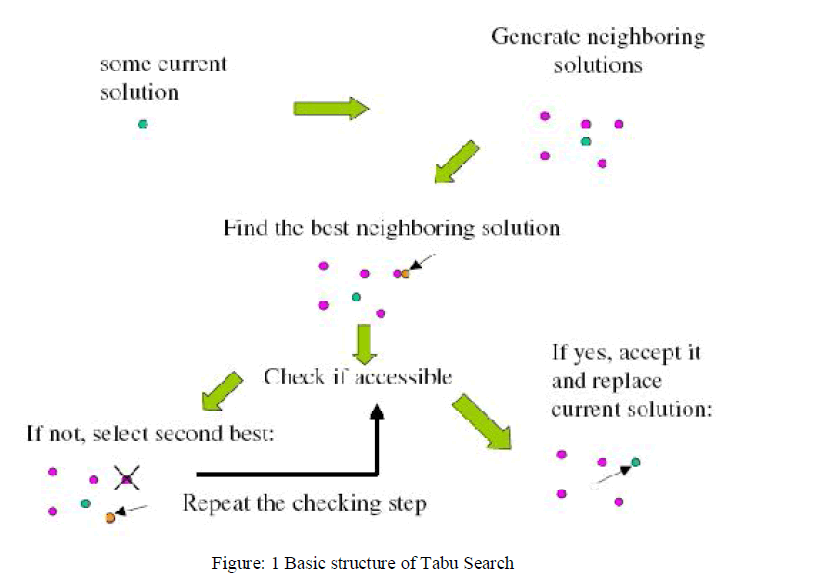 |
III. PROBLEM DESCRIPTION |
| There are no measures about the cross over connection between nodes as well as the efficiency in providing the result seems to be not much greater. Execution time and resource used seems to be another key problem. Determine function such as size of tabu list. As optimize the solution stands as a key challenge because the traveling salesman is NPHard problem. NP-hard problem is solution in polynomial sequence there is a difficulty in finding optimal solution. Combinatorial optimization consists of finding an optimal object from a finite set of objects. In many such problems, exhaustive search is not feasible. It operates on the domain of those optimization problems, in which the set of feasible solutions is discrete or can be reduced to discrete, and in which the goal is to find the best solution |
IV. OVERALL SYSTEM PROCESS |
| Input sample is passed to the system is the first step, then implementation of the algorithm proceeds Details of benchmark problem Dataset collection consist of analysis of varies benchmark problem related to ravelling salesman problem such as dantzig42 is a set of 42 cities, from tsplib. The minimal tour has length 699. Fri26 is a set of 26 cities, from tsplib. The minimal tour has length 937. P01 is a set of 15 cities, can be used in the project to obtain optimal solution. The performances of the algorithms were computed and compare their performances. |
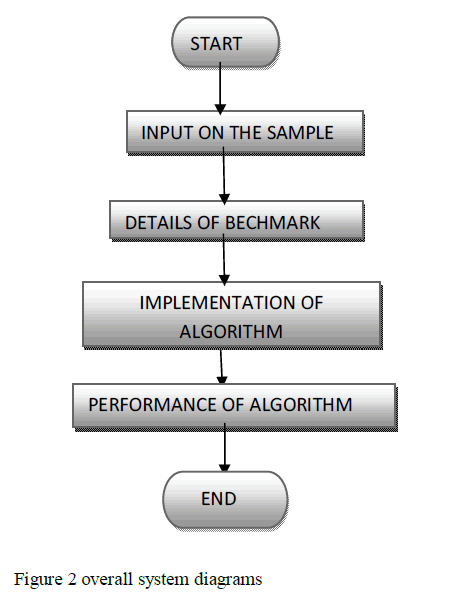 |
V. PROPOSED BIO INSPIRED ALGORITHM |
| Evolutionary algorithms are based on the laws of evolution of spices. Implementation of bio inspired algorithms such as ant colony optimization, bee colony optimization, cuckoo search optimization were used to perform comparison between these three algorithms has been made, concluding that the choice of algorithm is influenced by the priorities of the user. In computer science and operations research, the ant colony optimization algorithm (ACO) is a probabilistic technique for solving computational problems which can be reduced to finding good paths through graphs. This algorithm is a member of the ant colony algorithms family, in swarm intelligence methods, and it constitutes some Meta heuristic optimizations his shortest route can be built from the strongest segments of the best solutions. Bee colony optimization algorithm mimics the food foraging behaviour of swarms of honey bees. Cuckoo search (CS) is an optimization algorithm it was inspired by the obligate brood parasitism of some cuckoo species by laying their eggs in the nests of other host birds. |
VI. CONCLUSION |
| The proposed system focuses on the issues in metrics such as nearest neighbour node in rule specification and implementation of nearest node in a travelling salesman problem by using suitable benchmark problem. The main focus on this project is to the insertion of nodes, finding nearest neighbour node. In travelling salesman problem, bio inspired algorithms such as cuckoo search optimisation, ant colony optimisation, bee colony optimisation algorithms were carried out and their performances were calculated and compare its solutions and find an appropriate optimal solution. |
References |
|